波形钢腹板变截面梁剪力滞的差分解

王庆丰 向阳开

(重庆交通大学土木建筑学院，重庆 400074)

1 概述

20世纪80年代末期，法国首先建成世界上第一座波形钢腹板箱梁桥Cognoc桥，随着该桥梁结构的应用，各国都相继开始展开相关研究，并迅速推广开来，我国一些科研单位和高等院校也开展了波形钢腹板箱梁桥的力学特性研究和桥梁的设计与建造工作。

波形钢之所以能够在桥梁中得以成功应用，在于它能以波形钢替代一般混凝土箱梁的腹板而减轻结构自重，同时由于其褶皱效应，在纵桥向腹板的轴力很小，波形钢对整体箱梁刚度的影响，忽略其对箱梁承载能力的贡献，认为只有顶板和底板承受很大的应力，如图1所示。本文也是在此基础上作进一步分析。

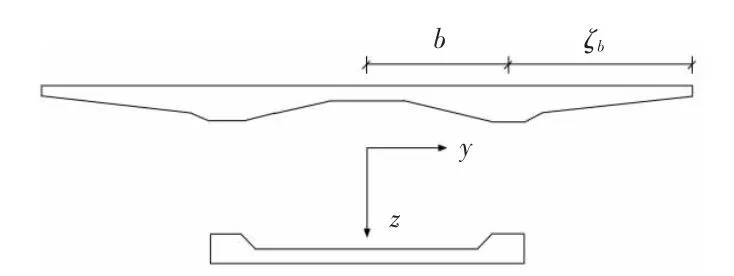
图1 不计波形钢腹板抗弯作用的结构示意图

目前针对波形钢腹板梁桥剪力滞的研究大都集中在等截面简支梁，文献［3］分析了变截面悬臂梁的剪力滞问题。波形钢腹板变截面连续梁桥已经开始建设，针对其剪力滞的求解大都通过将结构转化为简支结构，然后通过解肢法或叠加原理求解。将结构体系转化为简支体系后，简支体系仍为变截面，因此针对变截面简支梁的剪力滞效应求解尤为重要。

基于以上，提出对波形钢腹板变截面简支梁桥的剪力滞的分析，利用差分法建立矩阵方程［G］{U}=［F'(x)］，然后再对F'(x)利用差分法求解，最后得到U，进而求得各个截面的剪力滞。分析其分别在集中荷载，均布荷载的作用下其剪力滞纵向分布情况。在对F'(x)的求解中利用函数求导法，使剪力滞求解更加精确。

2 公式推导

利用文献［3］推导的波形钢腹板剪力滞的微分方程及边界条件。

微分方程和变分条件:

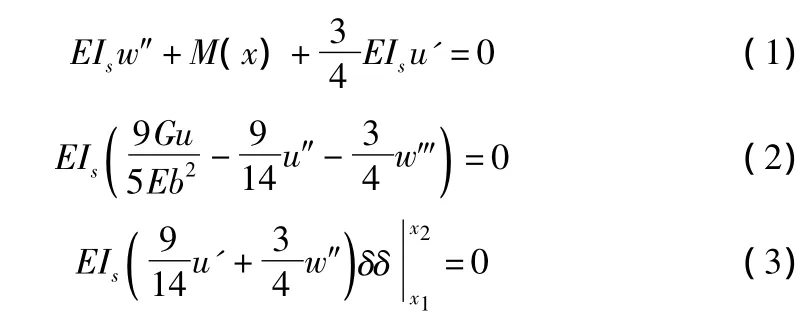
在支座边缘处的边界条件为:

对于变截面而言，Is是变化的，因此取为I(x)。式(1)左右两边除以EI(x)，然后对x求导得到，并将其代入式(2)得到:

其中，

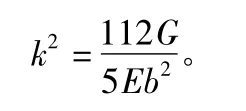
利用差分法，将 U″(x)代入式(6)

并利用边界条件式(4)，可得到矩阵表达式如式(7)所示，简写成［G］{U}=［F'(x)］。

3 计算思路

1)确定截面材料特性和几何特性，并求出梁全长弯矩和惯性矩的变化规律，并建立函数M(x)，I(x)。

3)求 U'(x)。

4)代入式(5)求出各个截面的剪力滞。

4 计算分析

1)拟定梁的尺寸。

如图2～图4所示，梁长2 000 mm，混凝土为C40，钢腹板采用A3钢，为便于计算，顶板和底板的混凝土均采用等厚度。底板线性为二次抛物线。

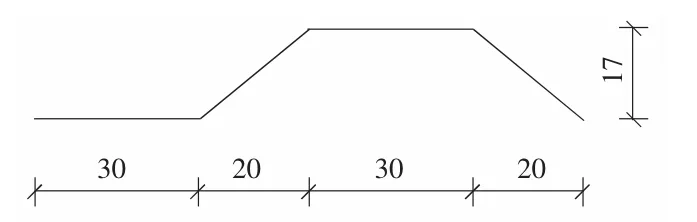
图2 腹板尺寸（单位：mm）

2)数值计算。

将梁分成20份，建立F'(x)的函数式，由矩阵表达式可看出只有M(x)和I(x)是变量，因此只需求出二者的表达式即可。

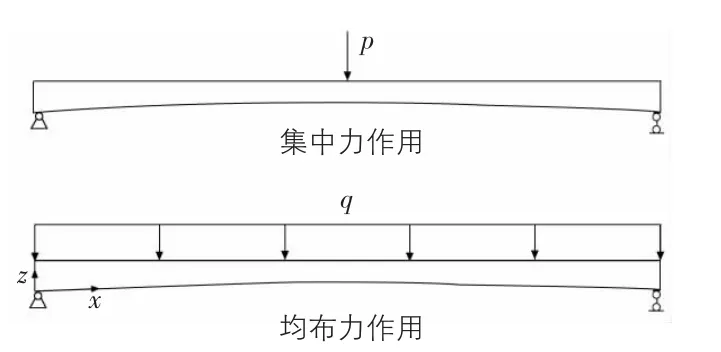
图3 荷载作用

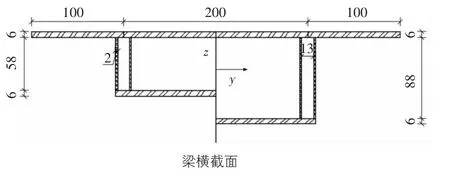
图4 横截面尺寸

以左支点为坐标原点可以得到抛物线函数Z(x)，根据材料力学和几何关系建立惯性矩方程I(x)。

利用Matlab进行矩阵运算求解梁纵向不同位置的Ui，并将Ui代入剪力滞公式来求解各个截面的剪力滞(本例所求的剪力滞均为腹板与顶板交界处的值)，如表1，表2所示。其中支点截面为0号截面，剪力滞结果关于跨中对称，因此表中仅仅列出半跨值。

表1 集中力作用下的剪力滞

表2 均布荷载作用下的剪力滞

3)ANSYS分析对。

为评价数值计算的精确性，采用ANSYS对模型梁进行模拟分析。其中混凝土采用Solid65单元模拟，钢腹板采用Shell181单元模拟，有限元模型如图5所示。顶板与腹板交界处的剪力滞见表1，表2。对比可得在集中力作用下差分解和有限元解最大相差10.8%，均布荷载作用下的剪力滞最大相差14.2%，并且具有有限元解全部大于差分解的规律。因为在文献［1］的公式推导和本文的差分计算的过程中，均忽略了腹板刚度对整体的影响，因此差分解计算的结果会偏小。在实际应用过程中可以考虑乘以1.1的增大系数。

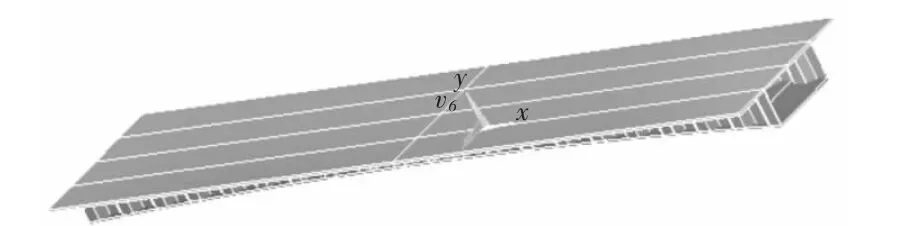
图5 有限元模型

5 结语

差分法在波形钢腹板变截面桥梁剪力滞计算的运用中，通过数值计算和有限元对比分析，整体差分解比有限元解偏小，最大相差14.2%，这主要是由于在文献［1］的公式推导和本文的差分计算的过程中，均忽略了腹板刚度对整体的影响，因此差分解计算的结果会偏小，可以得到很好的吻合结果。

［1］陈宝春，陈宜言，林 松.波形钢腹板桥梁应用调查分析［J］.中外公路，2010，30(1):109-118.

［2］项海帆.高等桥梁结构理论［M］.北京:人民交通出版社，2001.

［3］冀 伟，蔺鹏臻，刘世忠，等.波形钢腹板箱梁剪力滞效应的变分法求解［J］.兰州交通大学学报，2010，29(6):16-19.

［4］周茂定，刘世忠，杨子江.波形钢腹板组合箱梁剪力滞效应的比拟杆法求解［J］.兰州交通大学学报，2012，31(4):41-44.

［5］季立东.基于悬臂波形腹板箱梁剪力滞效应的力学特性及试验研究［D］.南京:南京航空航天大学，2008.

［6］吴文清.波形钢腹板组合箱梁剪力滞效应问题研究［D］.南京:东南大学，2002.