Boltzmann 模型在高速铁路路基沉降预测中的应用

徐卫平 赵松琴 吴 勇

(三峡大学土木与建筑学院，湖北宜昌 443002)

1 概述

路基在荷载作用下，沉降将随时间发展，其发展规律主要是通过以下两大类方法来加以描述。第一类是以固结理论及各种土的本构模型为基础的计算沉降量的各种有限元法;第二类是根据现场实测资料来推算沉降量与时间关系的预测方法［1］。但是由于固结理论的假设条件以及确定计算指标在试验技术上的一些问题，因而在一般工程设计中难以采用，使得实测路基沉降过程数据在某种意义上较理论计算更为重要和实用。

目前常见的沉降预测方法主要有双曲线法、指数曲线法、抛物线法、三点法、沉降速率法、星野法、Asoaka法、泊松曲线法、灰色理论和人工神经网络等。由于每种沉降预测方法都有一定的适用范围，需要结合具体的工程项目中沉降变形的特点，选择合适的预测方法进行沉降预测分析。针对这个问题，本文结合高速铁路路基工程实例，采用Boltzmann模型，对路基后期及最终沉降进行预测。实例研究表明该预测模型具有较好的精度和适应性。

2 路基沉降变形的“S”形特征

路基的沉降按其发展可以分为瞬时沉降Sd(t)、固结沉降Sc(t)和次固结沉降Ss(t)三部分。合理的沉降监测数据曲线应表现为“S”形［2］，即随着加载过程路基沉降可分为四个阶段:

1)发生阶段:路基刚填筑时，土体尚处于弹性状态，路基沉降量随荷载的增加呈近似线性增减。

2)发展阶段:随着路基填筑，荷载的不断加大，使其逐步进入塑性状态。随着塑性区不断开展，路基沉降速率也不断增加，直到荷载不再增加为止。

3)成熟阶段:当路基填筑完成，部分尚未完成的固结和土体的流变导致沉降随着时间的推移而继续，但沉降速率递减。

4)到达极限:随着时间的不断延长，沉降速率快速减小并趋于稳定。

3 Boltzmann预测模型的建立与分析

3.1 模型的建立

在时间预测序列中，Boltzmann模型的表达式为:

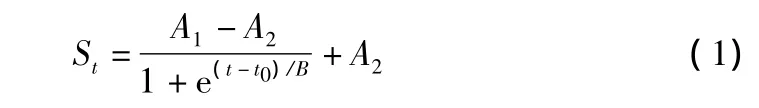
其中，St为t时刻对应的预测值，其单位为长度单位;t为时间;B为待定参数且为正;A1为最小值;A2为最大值;t0为当St=(A1+A2)/2时所对应的时间，B为无量纲，A1，A2单位为长度单位(见图1)。

3.2 模型的特点

Boltzmann预测模型具有以下3个特点，分别为:

1)单调递增性，随着时间t的增长，St也不断增长，即:

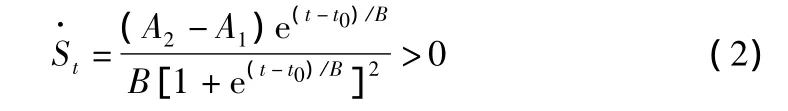
2)有界性，当时间t趋于无穷大时，St趋近于A2，即:

3)呈“S”形，存在拐点，该曲线对时间 t呈“S”形，即:

图1 A1，A2和t0的含义

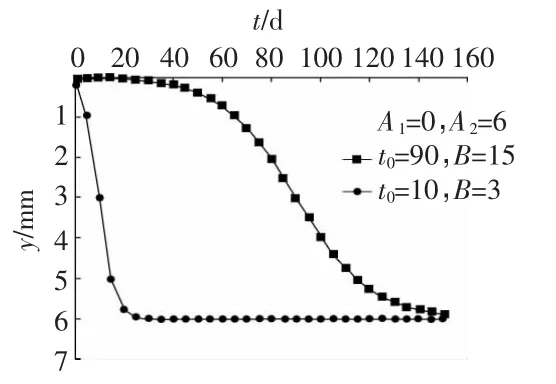
图2 Boltzmann预测模型适应性判断

表1 路基沉降实测值与时间关系

显然t=t0时，曲线开口凹向上方;当 t＞t0时＜0，曲线开口凹向下方，所以呈“S”形。

4)良好的适应性，确定参数A1，A2之后，通过调节t0和B的值可以模拟相当大范围的曲线，如图2所示。

3.3 模型参数的求解

Boltzmann预测模型含有3个未知参数A1，A2，B，t0可以通过A1和A2求得。本文采用高斯—牛顿迭代算法求得各参数的最优估计，通过此方法获得Boltzmann预测模型参数的最小二乘无偏估计［6］。

4 工程实例

4.1 实例介绍

时速350 km/h的沪昆客运专线杭长湖南段线路通过的地区多为岩溶地基、黄土地基、软土地基等不良地层和特殊地层。全段路基工程15.33 km，占线路总长度的16%，线路均为无砟轨道，地基的处理方式有换填、打入桩和CFG桩等。由于高速行车要求路基提供一个高度平顺和稳定的轨下基础，所以控制路基的沉降变形成为路基设计的关键。因此在路基线下工程施工过程中，必须加强现场沉降观测和实验分析，掌握工程特性的变化规律，及时验证并修正理论计算结果，确保线下工程沉降变形满足无砟轨道铺设条件［7］。

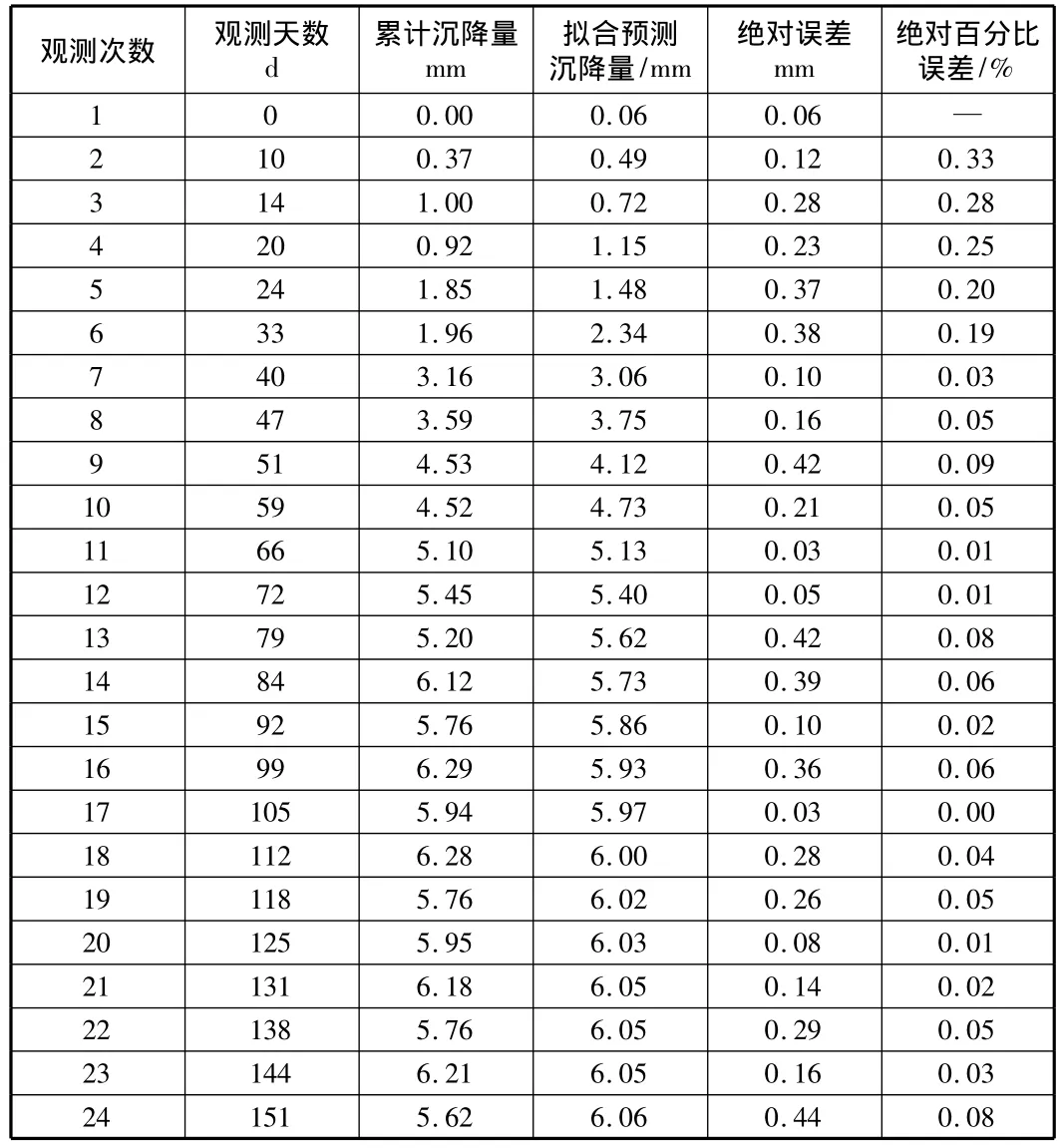
表2 路基沉降预测值与实测值对比表

4.2 预测分析

选取DK876+301断面处的沉降观测值，以2011年10月～2012年2月的沉降实测数据为基础，采用高斯—牛顿迭代算法，利用MATLAB编写程序，对Boltzmann预测模型各参数进行最优估计，然后再对指定时间点沉降及最终沉降进行预测［3］。参数的计算结果为:A1= －0.52，A2=6.06，t0=37，B=15.94，代入式(1)得:

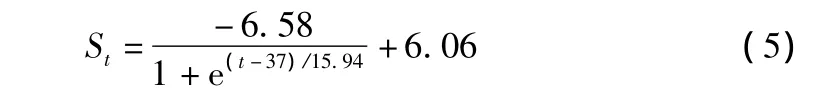
应用式(2)拟合预测各时间点的沉降量，路基沉降实测值与时间关系见表1，路基沉降预测值与实测值对比如表2，图3所示。

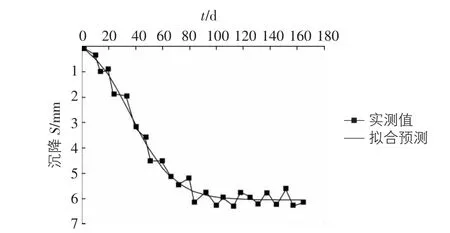
图3 路基实测沉降与预测沉降（S—t）曲线对比图

预测稳定后的 250 d，500 d的沉降量分别为 6.06 mm，6.08 mm，说明该路基沉降已经稳定。预测数据的绝对误差小于0.5 mm，相关系数达到0.98，说明Boltzmann预测模型具有较高的精度。

5 结语

1)Boltzmann预测模型所预测的路基沉降量与时间的关系曲线和路基实测沉降变化规律相一致，都呈“S”形，符合全过程的沉降量与时间的关系，说明该模型能够反映路基沉降量与时间的关系［4］。2)实测沉降值与预测沉降值较吻合，表明Boltzmann预测模型能够较准确地对路基最终沉降进行预测，能够满足工程精度要求，可以为高速铁路路基沉降预测提供有效地参考［8］。

［1］宰金珉，梅国雄.全过程的沉降量方法研究［J］.岩土力学，2000，21(4):322-325.

［2］梅国雄，宰金珉，殷宗泽，等.沉降时间曲线呈 S形的证明——从一维固结理论角度［J］.岩土力学，2004，25(1):20-22.

［3］潘林有，谢新宇.用曲线拟合的方法预测软土地基沉降［J］.岩土力学，2004，25(7):1053-1058.

［4］余 闯，刘松玉.路堤沉降预测的Gompertz模型应用研究［J］.岩土力学，2005，26(1):82-86.

［5］雷长顺，肖世伟.高速铁路预应力管桩地基沉降理论分析与计算［J］.山西建筑，2012，38(3):146-147.

［6］夏元友，刘 鹏，莫介臻.高速公路软基沉降预测系统及其应用研究［J］.公路，2005(8):275-279.

［7］王炳龙.高速铁路软土路基工后沉降的预测与控制［D］.上海:同济大学博士学位论文，2003.

［8］铁建设［2006］158号，客运专线铁路无砟轨道铺设条件评估技术指南［S］.