最大熵拟合概率密度函数在可靠度计算中的应用
汤保新 潘永强 路培国
(1.扬州大学土木工程系,江苏 扬州 225127;2.江苏省建筑设计研究院,江苏 南京 210000)
结构可靠度计算常用的方法有一次二阶矩法[1],有条件则采用高次高阶矩法以提高计算精度,如二次二阶矩法与二次四阶矩法,这类方法需要计算功能函数的偏导数,计算采用迭代法,计算结果为可靠指标,不是直接的失效概率,而且随着功能函数的非线性程度的增大,计算精度有所减小。结构可靠度的计算也采用蒙特卡罗法,计算量大,一般用于各种可靠度近似方法的校核。当极限状态函数有显式表达式而且随机变量不多的简单情况,亦可采用数值积分法,但当失效区域是一般不规则或是多连通或不连通的独立区域时,数值积分法亦有一定困难。如果可以求得极限状态函数的前几阶矩(一般为四阶矩或五阶矩),则可采用拟合概率密度函数方法近似计算失效概率。拟合的函数有最大熵密度函数[2]和多项式密度函数[3],前者物理意义明显,计算较复杂,后者没有直接的物理背景,计算较简单。
本文对极限状态函数求得前几阶矩,再用最大熵法拟合其概率密度函数,近似计算失效概率。
1 近似计算失效概率的步骤
1.1 极限状态函数的前几阶矩
已知极限状态函数为Z=g(X)=g(x1,x2,…,xn),随机向量X的概率密度函数为f(X),则Z的各阶原点矩为:

式(1)可通过数值积分求得。f(X)可视为权函数,采用高斯积分法,计算效率和精度较高。如正态分布、指数分布、均匀分布,相应的权函数为 e-x2,e-x,1,可分别选高斯·埃尔米特(Gauss-Hermite)、高斯·拉盖尔(Gauss-Laguerre)、高斯·勒让德(Gauss-Legendre)积分点。
显然,这里规定m0=1是合理的。
1.2 用概率分布函数的多项式逼近极限状态函数
根据最大熵原理,极限状态函数的概率密度函数为:

式(2)中a0,a1,…,aN为待定系数;N为矩的最大阶数,一般取4~5阶矩即能获得良好的效果[2]。
这里,z的各阶原点矩也可采用积分形式表示为:

式(3)中待定系数有N+1个,方程有N+1个。
式(3)为非线性方程组,可转化为无约束优化问题,采用优化算法求解:

式(4)中ωk为加权系数,为使式(4)各项的量纲一致,可取ωk=。
优化算法的初始点可按正态分布给出,即:


解出待定系数,就可以得到概率密度函数。
1.3 计算失效概率
对式(2)积分得到极限状态函数的失效概率:

注意,实际问题的解应与用中心点法计算的可靠指标的近似值 β≈μz/σz,按正态分布换算的失效概率 Φ-1(- μz/σz)相差不会很大。
2 简单算例
例1:已知非线性极限状态方程g=567fr+0.5H2=0。f服从正态分布,μf=0.6,δf=0.131;r服从正态分布,μr=2.18,δr=0.03;H服从对数正态分布,μH=32.8,δH=0.03。试求失效概率[1]。
1)用数值积分求极限状态函数的前4阶原点矩:
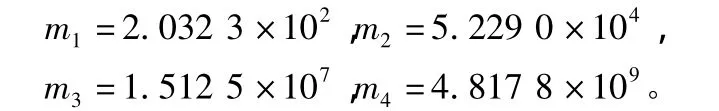
2)经计算,待定系数初始值为:

用优化算法求出待定系数:

3)求失效概率。这里的积分下界限取为μz-5σz=-320.870 9。失效概率Pf=0.025 951(换算为可靠指标β=1.944 0)。
作为对比,采用4阶原点矩计算的结果见表1。
例2:已知极限状态方程 g=1.8 - x1- x2=0,其中,x1,x2∈[0,1],其联合概率密度函数为 f(x1,x2)=2-x1-x2。试求失效概率[1]。
计算方法同例1,结果列于表1中。

表1 计算结果汇总表
3 结语
本文采用数值积分求得极限状态函数的前几阶矩,拟合极限状态函数的概率密度,求解失效概率。计算表明:1)采用四阶矩与五阶矩的计算结果相差不大,所以实用中可以采用四阶矩。2)数值积分的界限一般取为μ±5σ,即可满足工程精度要求。3)与多项式拟合法相比,计算精度变化较小,数值较稳定,所以适用性较好。
[1]赵国藩,金伟良,贡金鑫.结构可靠度理论[M].北京:中国建筑工业出版社,2000.
[2]章 光,朱维申,白世伟.计算近似失效概率的最大熵密度函数法[J].岩石力学与工程学报,1995(8):18-19.
[3]邓 建,李夕兵,古德生.结构可靠性分析的多项式数值逼近法[J].计算力学学报,2002(11):26-30.
[4]李庆扬,王能超,李大义.数值分析[M].武汉:华中工学院出版社,1982.
[5]王淑云,方保镕,王如云.数值分析方法[M].南京:河海大学出版社,1996.

