属性组合法反演Q 值的精度及其影响因素分析

蔡文涛，范廷恩，王宗俊

（中海油研究总院，北京 100027）

地震波在地下岩层传播过程中，能量一般随着传播距离的增加而减弱，造成衰减的因素主要有3类：球面扩散、吸收衰减和界面反射／透射损失等［1］。其中，介质的吸收衰减与频率有关。高频成分的衰减快于低频成分，这不仅造成了地震波总能量的损失，还会引起子波分辨率的降低。品质因子Q是表征介质吸收衰减特性的重要参量，同时也是地层含油气性的指示标志之一。因此，如何准确提取Q值是油气勘探地球物理研究的重点和热点［2］。

Q值提取方法可分为时间域和频率域两大类，主要有子波模拟法、振幅衰减法、上升时间法、解析信号法、频谱比法、质心频移法等［3－4］。近年来，还有学者尝试了一些新的方法，如刘国昌等［5］对正则化后的S 变换谱用谱比法提取Q值；Zhang等［6］根据Ricker子波峰值频率的移动从CMP 道集资料中反演Q值；高静怀等［7］利用匹配地震子波的峰值频率信息从零偏VSP资料中提取Q值，都取得了一定的效果。曹思远等［8］（2012）基于Kolsky－Futterman衰减模型，利用泰勒近似展开式，推导了频域近似属性组合Q值反演式（分一阶式和二阶式）。属性组合法与质心法类似，都是利用频域统计特征量的组合进行Q值反演，不同的是，该方法具有较严格的理论证明。需要说明的是，上述方法都是基于一定的假设前提，有各自的适用条件，到目前为止，尚没有一种方法具有普适性。

我们针对最新提出的属性组合法，通过模型数据试算，验证该Q值反演方法的可靠性。在此基础上，选取两种衰减模型和两类震源子波，以波谱不同的频带成分进行Q值反演，对比了谱比法、质心法和属性组合法的理论精度，并分析频段区间对于Q值反演的影响。最后，采用海上地震资料检测了属性组合法反演Q值的实际应用效果。

1 方法原理

假设地震波的传播过程由线性系统理论来描述，震源谱为S（）f；接收记录谱为R（）f；仪器与介质响应为G＊H（）f。则有

其中，G包括几何扩散、仪器响应、震源／检波器耦合特性、反射／透射系数等因素，假设该系数与频率无关，H（）f为地层吸收衰减项。

根据Kolsky－Futterman衰减模型，假设激发、接收点之间为常Q介质，则有

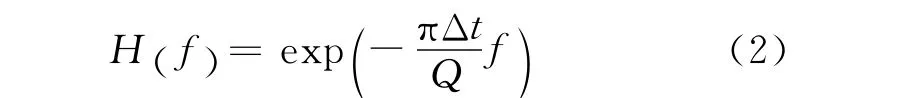
其中，Δt为传播旅行时，为品质因子。

对于任意频谱A（）f，定义高阶矩属性，则有

其中，k＝1，2，3，…。当k＝1时为质心频率；当k＝2时，为转动频率（与转动惯量有关，又称为惯心频率）。

定义方差为：

对（1）式作适当处理，则有

品质因子Q与ln［S（）f／R（）f］－f曲线的斜率成反比，拟合出斜率即可得到Q值。称该方法为谱比法。

假设震源谱为高斯谱，则有

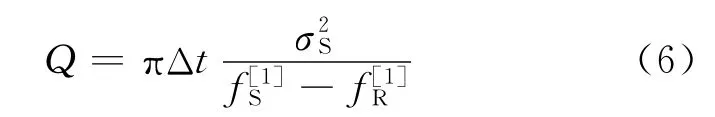
对于非高斯形状的震源谱，（6）式近似成立。称该方法为质心法。

对指数衰减项exp（－πΔtf／Q）作一阶和二阶泰勒近似展开，分别得到一阶和二阶Q值反演式（具体推导请参见文献［8］）。

一阶Q值反演式为

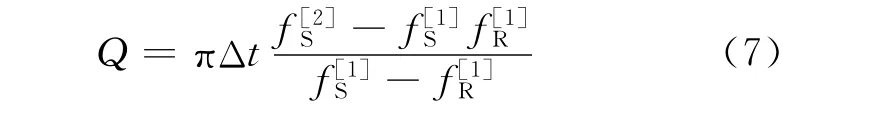
二阶Q值反演式为

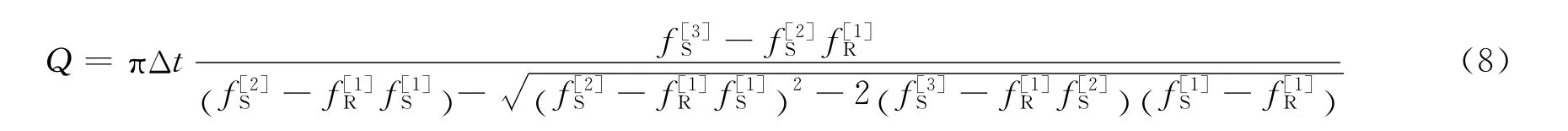
文献［8］中给出的二阶式为双解（另一解是根号前的“－”号换成“＋”号），根据笔者多组模型的验证结果发现，另一根恒为假根，可舍去。一般地，泰勒二阶展开式的精度高于一阶，因此（8）式的精度高于（7）式。由于一阶式和二阶式都是频域高阶矩属性的组合，将两式统称为属性组合法，从这个意义上讲，质心法也属于属性组合法的一种。

2 属性组合法可靠性模型测试

设计6层地质模型，各层厚度、速度及Q值分布见表1。震源子波选取50 Hz雷克子波，按照（2）式所示的衰减模型生成零偏VSP下行波数据，利用一阶式和二阶式反演地层Q值。

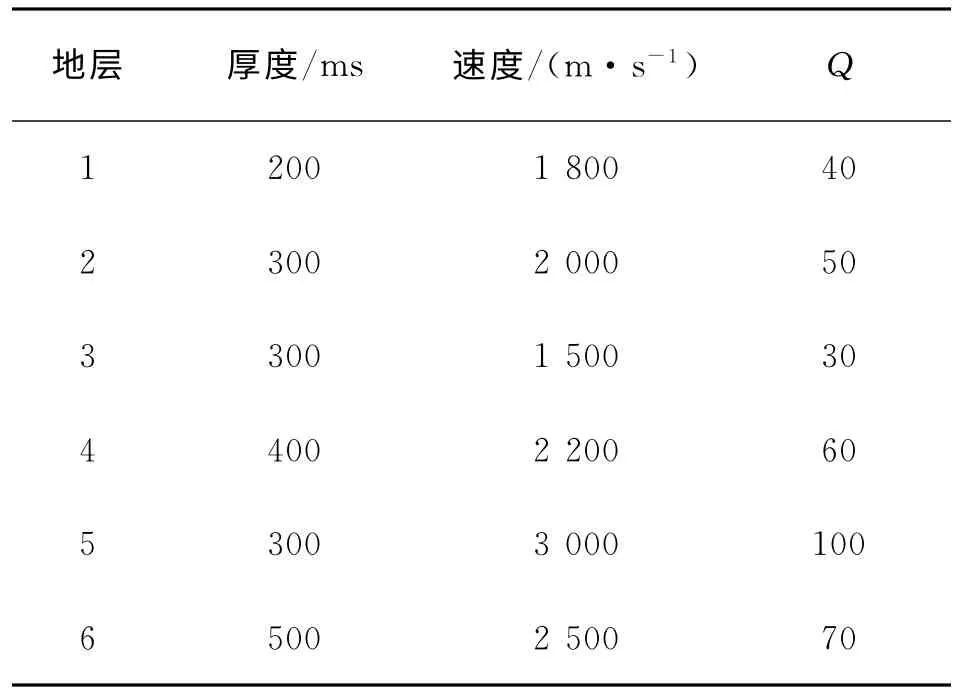
表1 层状模型数据

图1是Q值反演结果，可以看到，一阶式和二阶式都能较好地反演出地层Q分布；一阶式反演结果略大于真实值，二阶式反演结果与真实值吻合度较高。图2 给出了反演结果的相对误差曲线，两个反演结果的相对误差均在5%以内，表明一阶式和二阶式都具有较高的理论精度。从模型结果看，属性组合法的Q值反演结果具有一定的可靠性。

图1 模型数据属性组合法Q 值反演结果

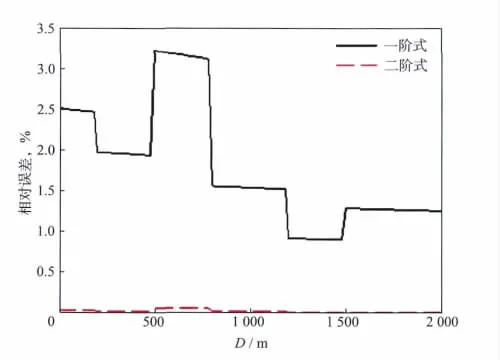
图2 模型数据属性组合法Q 值反演相对误差

3 不同Q 值反演方法对比分析

不同的Q值反演方法都是基于一定的假设（如震源、衰减模型等），其适用性不同。实际Q值提取中，由于信噪比等原因，一般不会选择全频段信息用于反演。例如，频谱比法反演Q值的稳定性不强，易受时窗的形状和长度、起止频段等因素影响［9］。武银婷等［10］在分析影响质心法应用效果的因素时，讨论了不同频带宽度对于Q值反演精度的影响。这里，通过几组模型分析，讨论在不同震源、衰减模型、频带范围下，谱比法、质心法和属性组合法反演Q值的理论精度。

首先，选取两个衰减模型（Kolsky－Futterman模型和Kjartansson模型，分别记为模型1和模型2），两类震源子波（雷克子波和多参数B 样条子波［11－12］，分别记为子波1和子波2）。

按Kjartansson模型，（2）式改写为

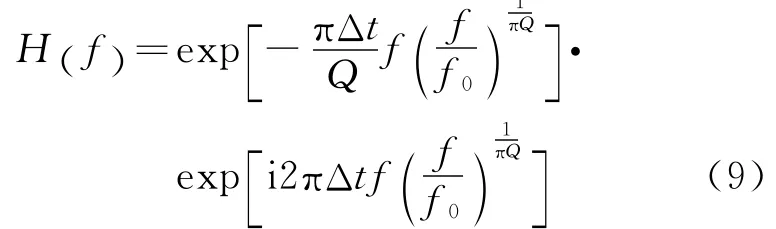
其中，f0为参考频率，这里取奈奎斯特频率。

图3给出了两类子波及其频谱。图3a中蓝色曲线代表50 Hz雷克子波（子波1），红色曲线代表宽带B子波（子波2）。

3.1 4组Q 值反演结果

图3 两类震源子波（a）及其频谱（b）

图4给出了对模型1和子波1（震源子波1按模型1衰减生成零偏VSP 下行波记录，在此基础上利用3种方法进行Q值反演，下同）分别采用3类方法反演Q值的相对误差（百分比值）。其中，图4a给出了采用谱比法反演Q值的相对误差；图4b给出了采用质心法反演Q值的相对误差；图4c和图4d分别给出了采用属性组合法一阶式和二阶式反演Q值的相对误差。图4中横轴代表频带下限f1；纵轴代表频带上限f2。如坐标（10，60）表示选择10～60 Hz宽度的频带提取Q值。从图4可以看出，对于模型1，反演精度从高到低依次为谱比法、二阶式、质心法和一阶式。不同频带对谱比法的反演结果影响不大。质心法在f1＋f2＝100 Hz曲线附近的反演精度较高，该频段恰好关于主频50 Hz对称，该区间的子波谱与高斯谱相似度较高，符合质心法对震源谱的假设，在低频段及高频段，波谱与高斯谱相似度降低，Q值反演精度相对降低；属性组合法（一阶式和二阶式）反演精度与频带的关系规律性较好，随着频带往低频移动，反演精度提高，这与属性组合法的推导有关，该方法基于指数衰减项exp（－πΔtf／Q）的泰勒展开，在Δt和Q固定的情况下，频率f越小，展式的误差越小，Q值反演精度越高。

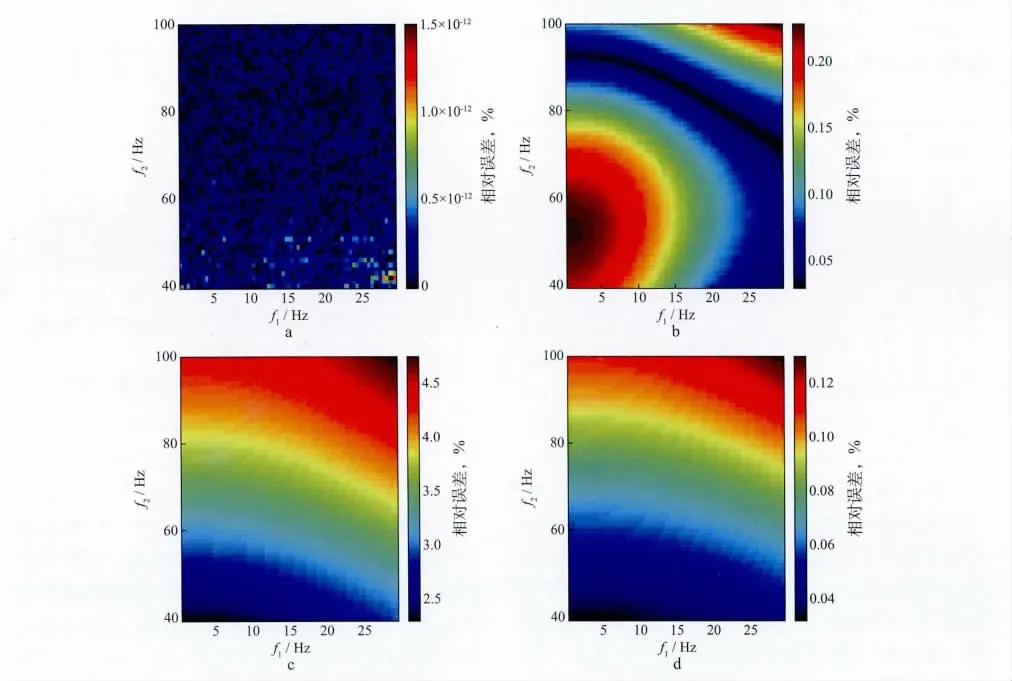
图4 对模型1和子波1采用3类方法反演Q 值的相对误差

图5给出了对模型1和子波2采用3类方法反演Q值的相对误差百分比，可见，谱比法、二阶式、质心法和一阶式的反演精度依次降低。频带对谱比法和属性组合法反演精度的影响与第1组类似，不同的是，质心法在低频段精度较高，这与宽带B子波谱在低频段与高斯谱相似度高有关。

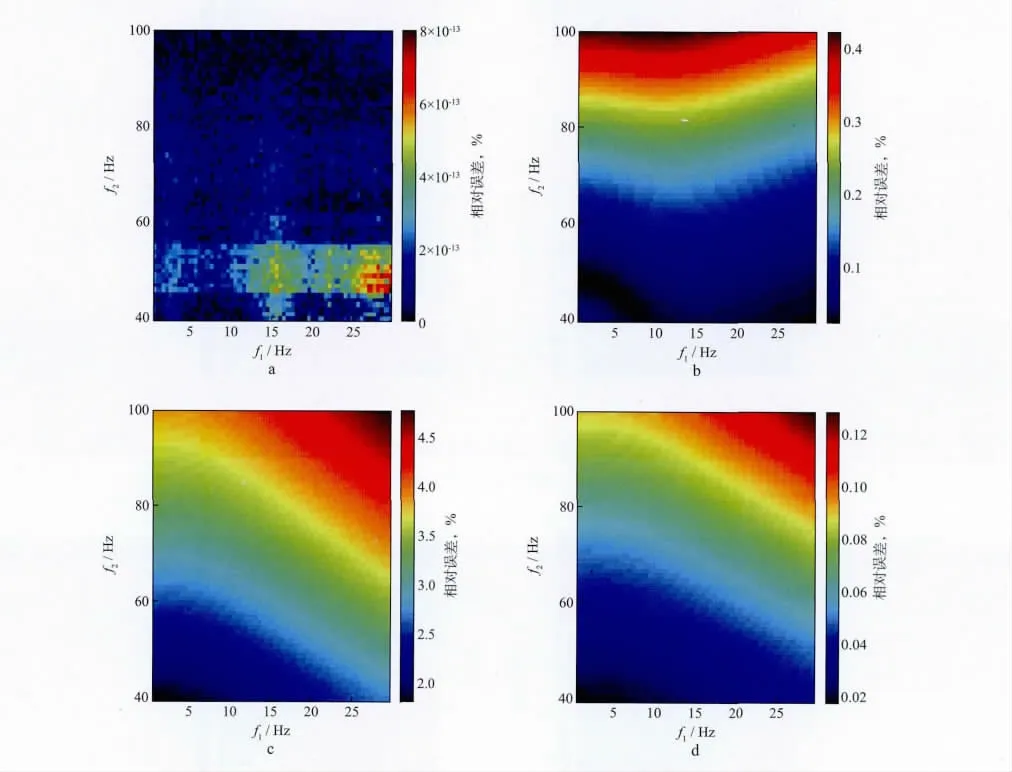
图5 对模型1和子波2采用3类方法反演Q 值的相对误差

图6给出了对模型2和子波1采用3类方法反演Q值的相对误差百分比。由图6 可见，谱比法、质心法、二阶式的反演精度相当，且都随着频带往高频移动精度提高；一阶式的精度相对较低，随频带变化的规律相反。这是因为模型2 与模型1的差异引入了新的误差，模型2对振幅谱的衰减项为，频率越高，与模型1越接近。谱比法、质心法和二阶式的误差主要来源于模型2与衰减模型假设的差异，一阶式的误差主要来源于频率的高低。

图7给出了对模型2和子波2采用3类方法反演Q值的相对误差百分比。由图7 可见，不同频带对反演结果的影响与第3组类似。

3.2 3类方法对比分析小结

对比第1 组和第2 组Q值反演相对误差表明，对于Kolsky－Futterman衰减模型，谱比法的精度最高，质心法的精度依赖于选取频带内的波谱形状，属性组合法的精度依赖于选取的频率高低。

对比第1组和第3组，第2组和第4组Q值反演相对误差表明，3 类方法也适用于Kjartansson衰减模型，反演精度一般较Kolsky－Futterman衰减模型的低。谱比法、质心法和二阶式的误差主要来源于模型的差异，一阶式主要来源于泰勒展开的误差。

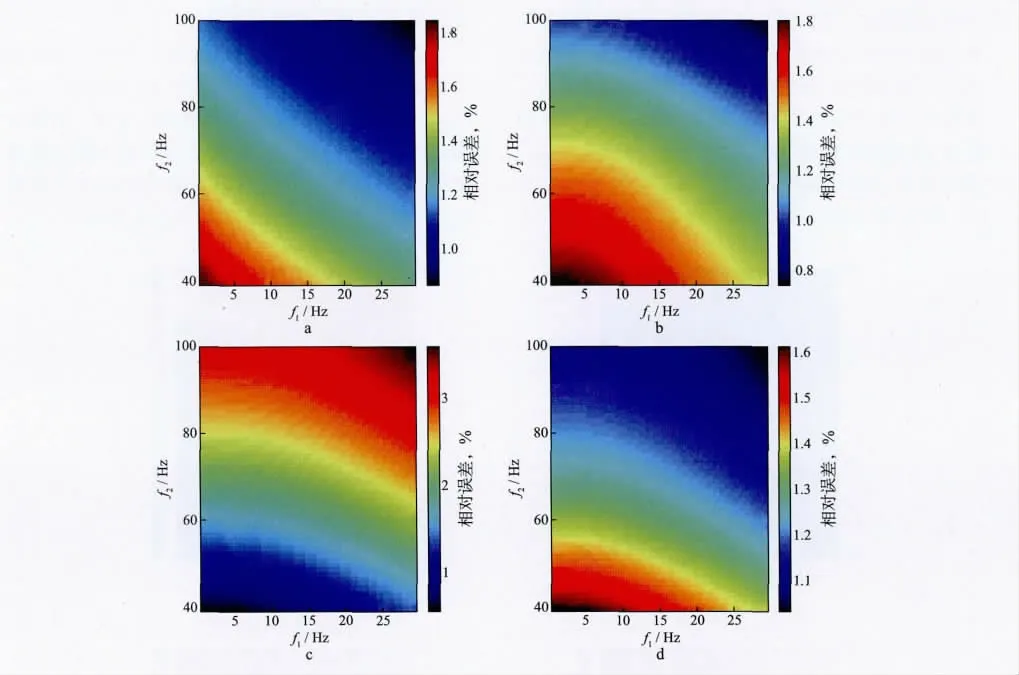
图6 对模型2和子波1采用3类方法反演Q 值的相对误差

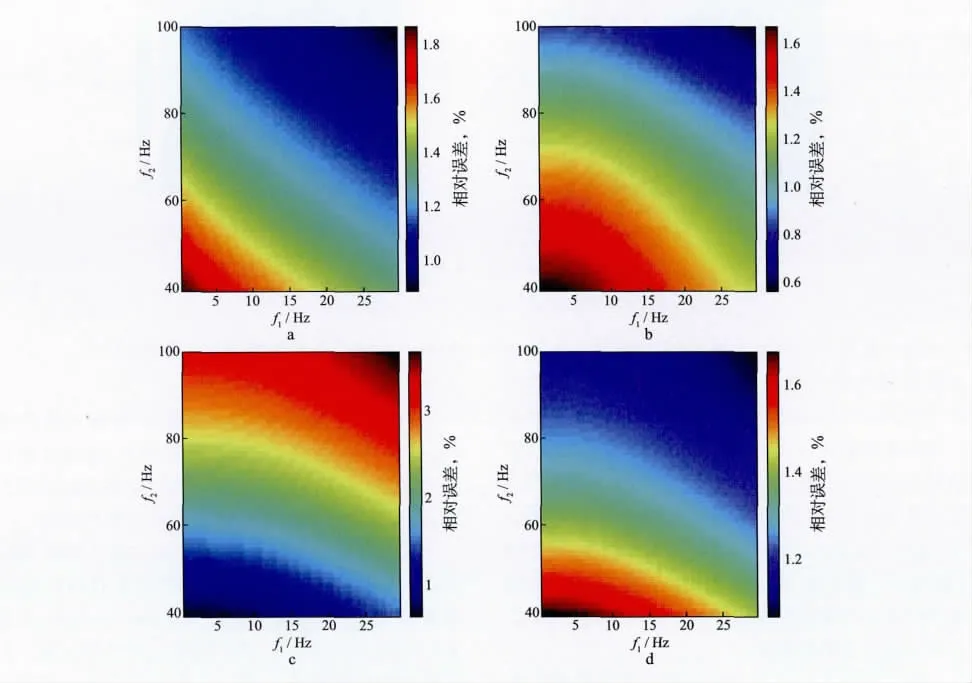
图7 对模型2和子波2采用3类方法反演Q 值的相对误差

对比第3 组和第4 组Q值反演相对误差表明，对于Kjartansson衰减模型，3类方法反演Q值的精度对震源子波的敏感性较低。

4 质心法与属性组合法的关系

虽然质心法和属性组合法推导的过程不同，但两类方法具有共同点，都是基于频域统计属性的组合式提取Q 值。对（6）式的作如下改写：

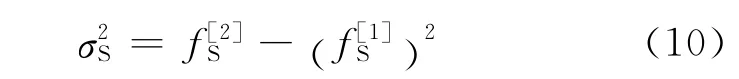
则质心法可表述为k阶矩属性的组合

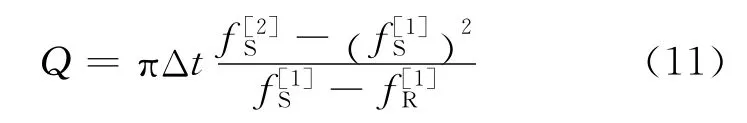
对比（11）式和（7）式发现，质心法与一阶式几乎一致。一般地，当时，一阶式提取的Q值大于质心法；当地层厚度较小时，，（11）式与（7）式相同，质心法可以看做一阶式的近似。

文献［12］在一阶式推导的基础上，给出了质心法的近似证明，其中，主要近似过程的数学条件是πΔtf／Q为小量。对该量作简单的估算：假设地层Q值为50；层速度为2 000m／s；检波器间 距 为20m；单程旅行时Δt为0.01s；地震频带取［0，150 Hz］；那么πΔtf／Q取值范围约为［0，0.1］，满足高精度泰勒一阶展式对变量的要求。由于该证明还作了其它的近似，使得质心法的精度随频带变化规律不同于一阶式。

从广义上讲，质心法可看作属性组合反演Q值方法的一种特例。

5 实际应用效果分析

图8是根据海上CDP资料应用二阶式提取的Q值分布，随着深度的增加，Q值呈逐渐增大的趋势，横向的起伏较小。将提取的Q值应用于该区地震资料的反Q滤波，处理前、后的剖面和频谱如图9所示。图9中的红色频谱为振幅谱，蓝色频谱为相位谱。从振幅谱上可以发现，反Q补偿后主频段［50Hz，140 Hz］的能量得到了较好的恢复，主频从48Hz提高到65 Hz，相位也得到了一定的校正。图10 是反Q补偿前、后剖面1 000～1 300ms 的局部放大结果，目的层在1 100～1 200ms，反Q补偿后的剖面同相轴变细，复合轴分离，断点清晰，分辨率提高，信噪比得到较好的保持，砂体之间的横向展布特征和纵向叠置关系更加清晰，为后期油田开发井网部署和井位优化提供了有利的依据。

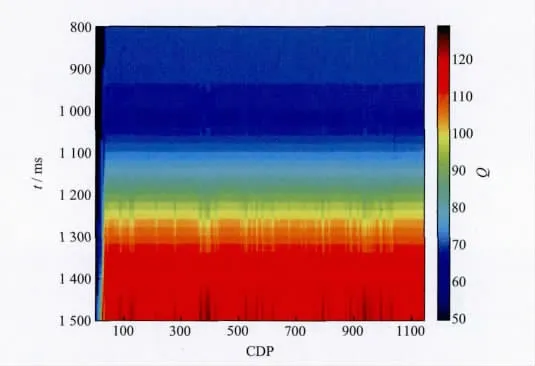
图8 属性组合法提取的Q 值分布

图9 实际海上地震资料反Q 补偿处理前（a）、后（b）剖面及其频谱

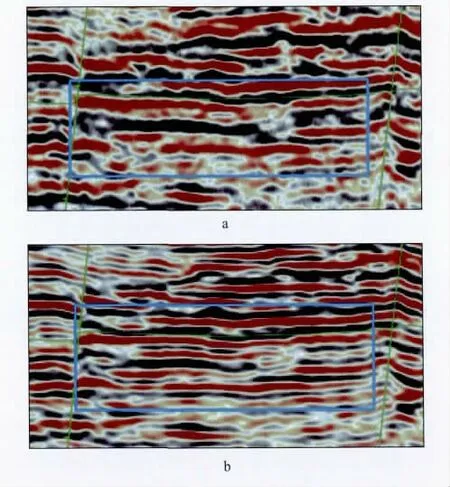
图10 反Q 补偿前（a）、后（b）剖面1 000～1 300ms局部放大结果

6 结束语

在对属性组合法（一阶式和二阶式）Q值反演的可靠性进行模型验证的基础 上，通过测试不同衰减模型、震源子波及频带宽度，对比了谱比法、质心法和属性组合法反演Q值的精度，分析出可能的影响因素。这些认识对于实际Q值提取方法的选择及应用，具有一定的参考价值。

另外，根据属性组合法的数学近似，可以预见，在小Q值情况下（如地表Q值提取等），其精度将受到较大的影响。如何适应小Q值提取，是属性组合法需要改进和研究的一个方向。

［1］王兆湖，刘财，王建明，等.叠后地震信号透射损失的补偿［J］.石油地球物理勘探，2008，43（2）：217－221 Wang Z H，Liu C，Wang J M，et al.Compensation for transmission loss of post stack seismic signal［J］.Oil Geophysical Prospecting，2008，43（2）：217－221

［2］马昭军，刘洋.地震波衰减反演研究综述［J］.地球物理学进展，2005，20（4）：1074－1081 Ma Z J，Liu Y.A summary of research on seismic attenuation［J］.Progress in Geophysics，2005，20（4）：1074－1081

［3］宫同举，孙成禹，彭洪超，等.几种提取品质因子方法的对比分析［J］.勘探地球物理进展，2009，32（4）：252－256 Gong T J，Sun C Y，Peng H C，et al.Comparison of several computational methods of quality factor［J］.Progress in Exploration Geophysics，2009，32（4）：252－256

［4］Tonn R.The determination of the seismic quality factor Q from VSP data：a comparison of different computational methods［J］.Geophysics Prospecting，1991，39（1）：1－27

［5］刘国昌，陈小宏，杜婧，等.基于整形正则化和S变换的Q 值估计 方法［J］.石油地球物理勘探，2011，46（3）：417－422 Liu G C，Chen X H，Du J，et al.Seismic Q estimation using S－transform with regularized inversion［J］.Oil Geophysical Prospecting，2011，46（3）：417－422

［6］Zhang C J，Ulrychz T J.Estimation of quality factors from CMP record［J］.Geophysics，2002，67（5）：1542－1547

［7］高静怀，杨森林.利用零偏移VSP 资料估计介质品质因子方法研究［J］.地球物理学报，2007，50（4）：1198－1209 Gao J H，Yang S L.On the method of quality factors estimation from zero－offset VSP data［J］.Chinese Journal of Geophysics，2007，50（4）：1198－1209

［8］曹思远，赵宁，袁殿，等.地震波品质因子研究新方法［C］／／中国地球物理年会论文集.合肥：中国科学技术大学出版社，2012：454 Cao S Y，Zhao N，Yuan D，et al.A new method to inverse Q［C］／／The Chinese Geophysics.Hefei：Press of University of Science and Technology of China，2012：454

［9］聂冀强.零偏VSP 资料的Q 值反演方法及应用［D］.北京：中国地质大学，2011 Nie J Q.Approaches and application of inversion Q value inversion in zero－offset VSP data［D］.Beijing：China University of Geosciences，2011

［10］武银婷，刘伊克，常旭.零偏VSP 反演Q 值CFS方法及影响因素研究［J］.地球物理学进展，2010，25（6）：1897－1904 Wu Y T，Liu Y K，Chang X.Study on CFS method in Q inversion using zero－offset VSP data［J］.Progress in Geophysics，2010，25（6）：1897－1904

［11］刘兰峰，曹思远，王鲁.四参数宽带B样条子波［J］.石油地球物理勘探，2011，46（2）：247－251 Liu L F，Cao S Y，Wang L.Wide－band B－spline wavelet with four parameters［J］.Oil Geophysics Prospecting，2011，46（2）：247－251

［12］袁殿.理论宽带B 子波及谱定量表征［D］.北京：中国石油大学（北京），2012 Yuan D.Wide band B－wavelet and its spectrum quantify characterization［D］.Beijing：China University of Pertroleum（Beijing），2012