地面微地震资料震源定位的贝叶斯反演方法

宋维琪，朱海伟，姜宇东，郭全仕，曹 辉

（1.中国石油大学（华东）地球科学与技术学院，山东青岛 266580；2.中国石油化工股份有限公司石油物探技术研究院，江苏南京 211103）

微地震监测研究的重点在于微地震事件的准确定位。影响精确定位的因素很多，主要包括速度模型建立精度、反演算法的适用性、正演算法的精度等方面［1－3］。高精度的反演研究，目前还主要以时差反演为主，通过模型校正和反演方法的研究来提高定位精度，其中又分为P波时差反演和P－S波时差反演［4－5］。

常规地震反演中，共轭梯度法、模拟淬火法、遗传算法等线性或非线性算法都能够取得较好的反演效果。但是，微地震反演中，由于信号的信噪比低，加上浅地表各种噪声的干扰，难以拾取准确的初至，使得单纯地移植这些反演方法无法取得满意的效果。一般来讲，线性反演方法速度快，效率高，但是易于局部收敛，对设定的初值要求高。非线性方法全局搜索能力强，但是算法设计比较复杂，反演参数越多，反演速度越慢［6］。

对地面微地震反演，由于实际接收到的检波器信号中有些道的同相轴信息基本缺失，使得能够用于反演的道非常少；其次，对于变量的一阶导数的求取也非常困难，主要是由于目标函数值对于参量的扰动非常不敏感，使得求导运算十分复杂。此外，不同变量的扰动，对于目标函数值的影响也不同，例如对于相同的变化量Δx，变量层速度v或水平距离r对目标函数的影响完全不同，使得迭代过程十分繁琐。

遗传算法是一种非线性反演方法，其独有的个体、种群概念保证了搜索的路径是多维的，可以避免单维搜索陷入局部极值。但是，遗传操作过程中主要算法参数的选择对于反演的影响很大，既影响反演速度，又影响反演精度。也就是说，在微地震事件反演中，如果任意定义反演的搜索范围，任意定义选择算子、交叉算子、变异算子、适应度函数、种群大小、遗传代数等，那么遗传算法反演的效率与精度都会发生很大的变化，也增大了反演结果的不稳定性。

地面微地震监测星形的观测方式和资料信噪比低的特殊性［7－8］，尤其是由于有用信号十分微弱，使得拾取的初至信息不准确，以往确定性的线性或非线性反演方法几乎不能取得可靠的反演结果。贝叶斯反演方法是把先验信息和后验信息结合起来的推理估计方法，可以更好地融合多方面先验信息实现后验信息的最佳估计。因此，结合地面微地震资料的特点，研究了地面微地震资料震源定位的贝叶斯反演方法。

1 方法原理

地面微地震监测采用多线观测，利用多线观测结果进行微地震事件的定位。根据全概率理论，可以把最终定位解做为事件A，每条线都以不同概率确定事件A。把各条线反演问题作为最终反演结果的一个划分即Bi（i＝1，2，…，M），其全概率公式为

式中：P（Bi）为先验概率，根据每条线的信噪比确定；P（A｜Bi）为后验概率。

贝叶斯反演理论把反演问题与观测数据信息、模型信息以及先验信息通过贝叶斯推理联系起来。贝叶斯反演有多种求解方法，其中最常用的是贝叶斯最大后验解方法。设G为微地震到时观测数据，X为待反演参数，模型误差与待反演参数的先验估计均为正态分布，对每条线反演求解，建立目标函数求取贝叶斯最大后验解［9］：

式中：F（X）为模型结果；XP为参数的先验估计值；CD和CM为模型误差与先验估计误差的协方差矩阵；λ为权重系数，λ＝CM／CD。目标函数S（X）的求解，就是在数据拟合（第1项）和先验估计（第2项）之间寻求一种折衷。权重系数越大，反演解越接近先验估计；反之，反演解越接近于不稳定的原问题。非线性反演问题权重系数的选取是一个广受关注的问题，在无法确定观测数据噪声的情况下，比较常用的有广义交叉验证（Generalized Cross－Validation，GCV）方法和L－曲线（L－Curve）方法等。我们采用赤池贝叶斯信息准则（Akaike's Bayesian information criterion，ABIC）来确定最佳权重系数。ABIC是基于相对信息熵理论而提出的权重系数选取方法，其最佳权重系数由最小化ABIC获得。ABIC的表达式为

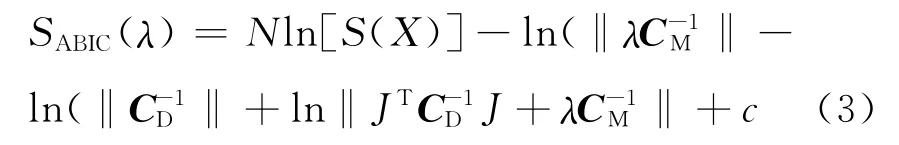
式中：N为CD的维数；J为雅可比矩阵；c为常数。实际求解时，首先选定若干λ值并求得相应的反演解，然后根据λ与反演解的值计算ABIC，ABIC 最小值对应的λ即为最佳权重系数。假定抽样计算独立，则评价函数如

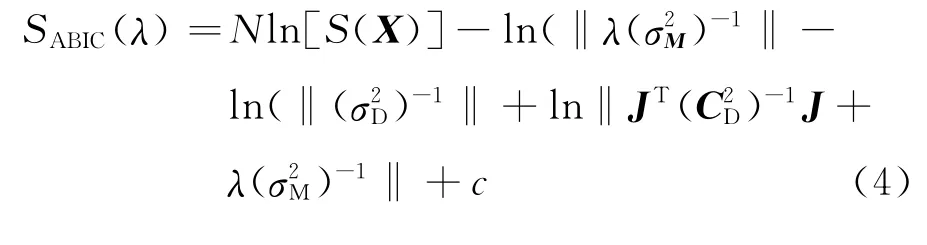
式中：σD，σM分别为理论模型和观测值残差的方差、模型参数的方差。这时，λ＝σD／σM。

对参数（速度、震源位置）的最优估计问题，等价为在贝叶斯理论下，具有先验信息条件时，经过贝叶斯推理，得到目标函数的极大后验概率。从公式中看到，目标函数的极大后验概率是理论模型和观测值残差、模型参数的参差极大后验概率的加权组合。实现时，通过抽样计算得到参数与速度参数模拟参差结果的先验分布p（Y，θ），确定θ的后验密度ρ（θ，Y）。设h（θ，Y）为θ和Y的联合概率密度函数，则

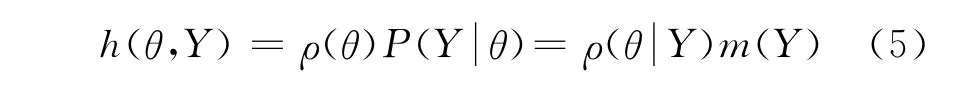
式中：m（Y）为Y的边缘密度函数，定义为

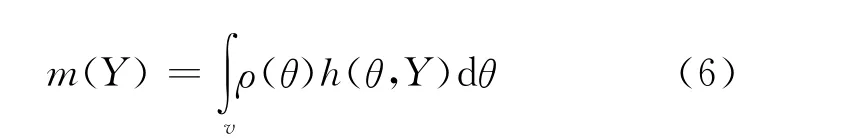
由（3）式和（4）式得

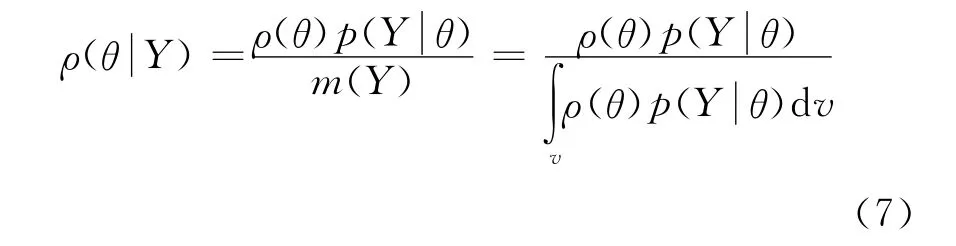
式中：p（Y）为样本Y＝（y1，y2，…，yn）的联合概率密度函数。

可见，θ的后验密度ρ（θ，Y）估计取决于先验分布ρ（θ）和已知θ情况下的样本的条件概率密度函数p（Y，θ）（或称为已知Y条件下，θ的似然函数）。p（Y，θ）通常采用模型的计算值与实测值残差的函数或者正态分布表示［10－11］，如

式中：σ2为残差的方差。

理论正态分布似然函数表示为

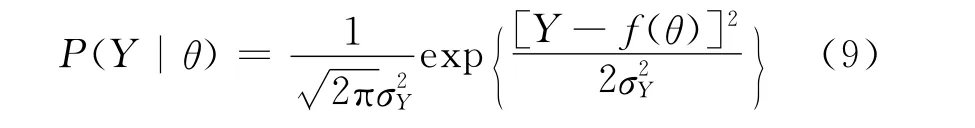
后验概率表示为

分析（10）式可知，在给定样本空间情况下，决定极大后验概率的是概率密度函数和分布函数的积分值。如果数据出现奇异，则积分结果奇异。因此，为了获得稳定的目标函数值，需要从计算的残差方差中利用回归方法或拟合方法得到理论模拟概率密度函数，然后计算后验概率，最后从不同速度模型对应的后验概率中取极大后验概率为目标函数结果。

2 寻优方法

公式（1）中右边第1项是一个有关地层速度和震源位置的多模态函数［12－13］，需要采用非线性法全局搜索算法来优化。为提高计算效率，采用极快速模拟退火方法加网格法的混合算法作为搜索方法。首先利用网格算法使搜索落入最优解所在的凸区间，再采用极快速模拟退火算法搜索最优解。这样既可以防止算法收敛于局部极值点，又极大地提高了算法的收敛速度。

3 建模方法

地面微地震走时记录由中深层速度变化较缓部分和浅地表速度变化相对剧烈部分组成。在反演时这两部分应分别对待，浅部采用横向变速模型，中深部采用水平横向均匀速度模型。在反演过程中，中深部数据和浅部数据可能会相互抑制，即浅部数据如果扰动剧烈，可能会把中深层的数据缓慢扰动淹没，使中深部反演变得迟钝。同样，中深部反演数据的扰动变化平缓，会影响浅部反演的敏感性。为此，反演迭代过程也分为两部分，即

式中：tl为理论计算的走时；tq为理论计算的浅部走时；ts为理论计算的深部走时，通过射线追踪正演计算。

计算浅部理论到时采用的近似方法为：假设浅部地层速度较低，地震波的射线路径与水平地面垂直，不考虑横向速度变化引起的射线路径的弯曲变化。

式中：hj为测井起始深度到高程参考基准面的厚度；hgc（x）为高程；vq为浅部速度模型。

目标函数（2）式相应地变化为

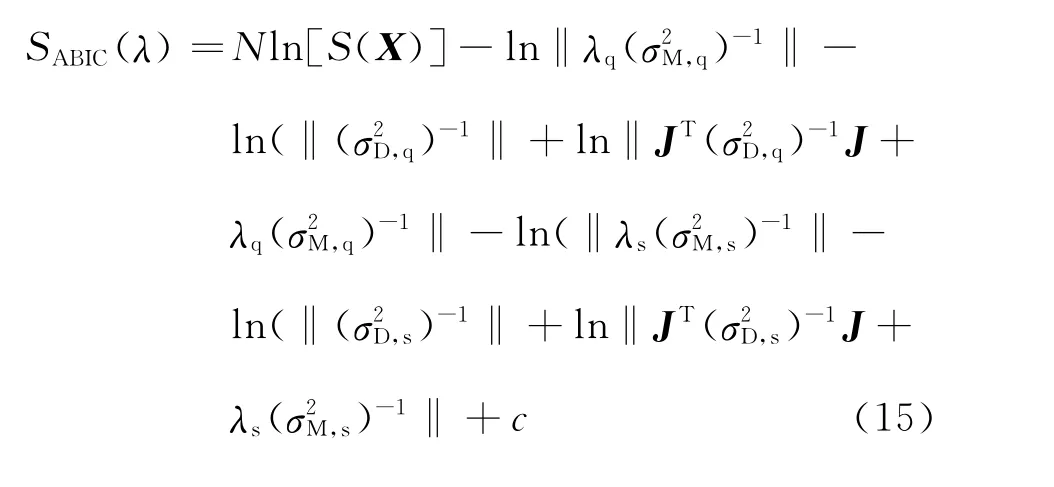
4 利用井资料和射孔资料反演初始速度模型

微地震压裂监测过程中，通常事先都要在压裂井段进行射孔以获取射孔事件记录。通过射孔记录到时和射孔点的已知位置进行速度模型的校正和建立，进而获取更加准确的初始速度模型。地面微地震监测不同于井中微地震监测，一般没有浅部测井资料。因此，地面微地震射孔资料不单是用来校正速度模型，还要用来进行浅部速度模型的建立。中深层初始速度模型资料一般由测井资料获得，而浅部速度资料通常难以收集，因此通过射孔反演方法求取浅部速度。求取步骤如下：

1）利用井资料建立中深层速度模型；

2）计算中深层模型的走时；

3）计算浅部走时

4）求浅部初始速度。

假定微地震波走时路径垂直水平面，则各接收点到参考面的初始速度为

至此，就建立了从浅部到深部整个速度初始速度模型。然后采用本文研究的贝叶斯反演方法进行速度模型的反演。具体的反演步骤：

1）在初始速度模型上进行速度参数的扰动调节

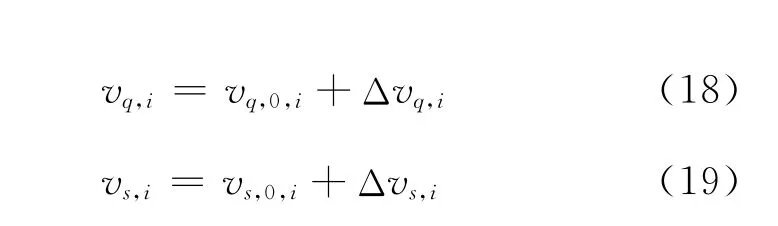
并计算其方差。

2）进行正演计算理论走时，然后计算观测到时和理论计算到时的残差与方差以及加权系数λq，λs。

3）对速度进行参数随机抽样，拟合（或回归分析）出一个理论残差方差的后验概率密速函数，即目标函数的后验概率密度函数、加权函数后验密度函数、速度参数方差的后验概率密度函数。通过以上各变量的函数求得雅可比矩阵。根据（15）式计算评价函数的极小值。此评价函数的极小值对应的速度参数就是反演结果。

4）反演每一条测线，得到了各线的浅地表速度模型和中深部地层速度模型。

5 微地震事件震源位置反演

通过测井资料和射孔资料反演出各条线整个地层的速度模型后，根据拾取的走时反演微地震震源位置。根据反演要求的不同，可以分为位置参数反演和速度、位置参数同时反演，我们只考虑位置参数反演。利用拾取的各条线到时和上面建立的速度模型，采用本文反演方法进行反演，得到震源位置。由于各条测线微地震记录的信噪比不同，拾取的到时和建立的速度模型精度不同，反演结果也不尽相同。综合各条线的反演结果，根据全概率公式推断估计最佳震源位置。

5.1 模型试验

设单个理论模型震源坐标为（200m，300m，2 000m），采用上文建立的速度模型进行反演。理论模型的走时利用射线追踪正演获得，并在理论走时中加上一定的扰动噪声。图1为我们研究的贝叶斯方法反演结果和以前方法反演结果的对比，可以看出，贝叶斯反演方法具有较好的抗噪能力。

图1 理论模型资料用以前方法反演结果（a）和贝叶斯方法反演结果（b）对比

5.2 实际资料反演

对实际地面微地震资料进行一定处理后，拾取有效事件的初至，结果如图2 所示。然后对利用射孔资料反演校正的速度模型进行反演。反演结果如图3所示。图3中红色和紫色的实点表示反演的2 个事件位置，浅蓝色的圈表示射孔点。反演结果和国外商业软件反演结果基本一致，如表1所示。

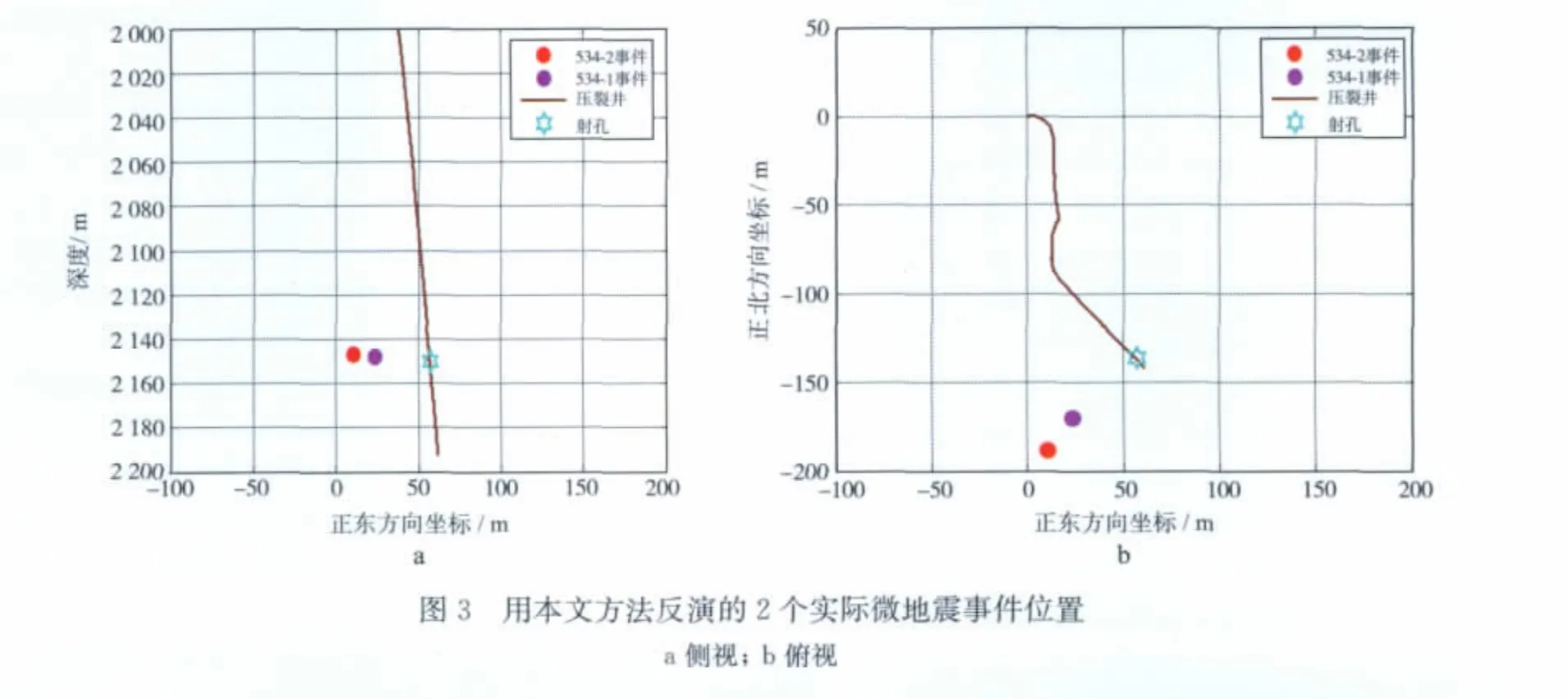
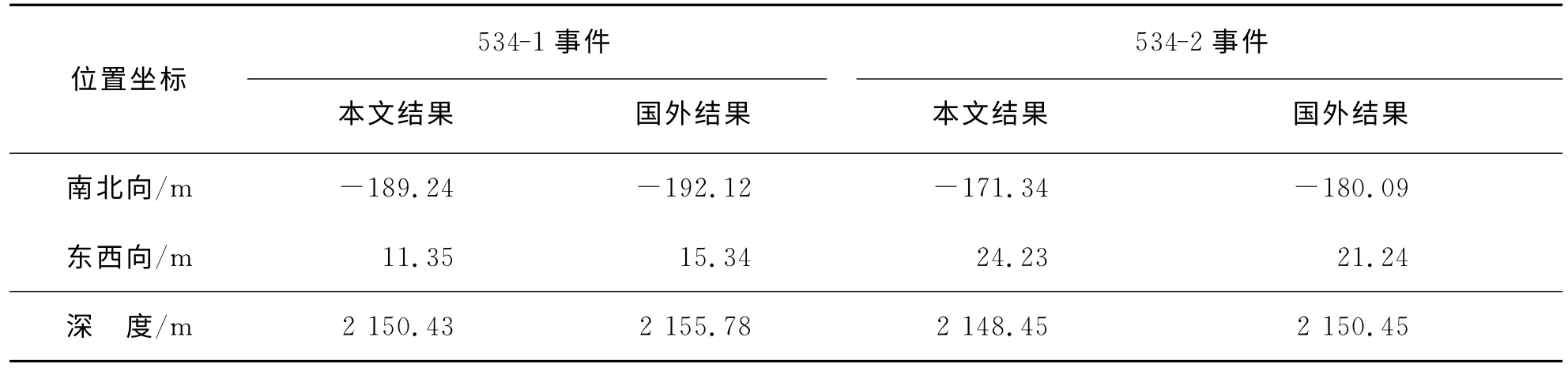
表1 2个实际微地震事件位置反演结果比较

6 结束语

地面微地震震源反演问题由于各种因素的影响和资料信噪比低，具有较大程度的不确定性。因此，将先验信息和后验信息结合起来进行最优解的评价，较好地实现了不确定性反演问题的寻优过程。将反演建模和迭代过程分为两部分进行，较好地解决了浅部和深部速度变化程度不同对反演解的影响。采用极快速模拟退火方法加网格法的混合算法作为搜索方法，网格法可以使搜索过程落入最优解所在的凸区间，而极快速模拟退火算法搜索最优解，既可以防止算法收敛于局部极值点，又能极大地提高算法的收敛速度。反演结果表明，反演方法在抗扰动噪声和解决不确定性方面具有显著优势。基于最大后验估计的贝叶斯反演方法对先验信息估计模型具有非常大的依赖性，因此，下一步对先验信息估计模型建立还需进行深入研究。

［1］Stoffa P L，Sen M K.Nonlinear multiparameter optimization using genetic algorithms：inversion of planewave seismograms［J］.Geophysics，1991，56（11）：1794－1810

［2］Pei D H，Quirein J A，Cornish B E，et al.Velocity calibration for microseismic monitoring：a very fast simulated annealing（VFSA）approach for joint－objective optimization［J］.Geophysics，2009，74（6）：47－55

［3］Lisbeth E S.Inversion of Arreal times of microearthquake sources in the noth sea using a 3－D velocity structure and prio information：part I［J］.Method Bulletin of the Seismological Society of America，1991，81（4）：1183－1194

［4］Willis R B，Fontaine J，Paugh L，et al.Geology and geometry：a review of factors affecting the effectiveness of hydraulic fracturing［R］.SPE Eastern Regional Meeting，97993－MS，14－16

［5］Chunduru R K，Sen M K，Stoffa P L.Hybrid optimization methods for geophysical inversion［J］.Geophysics，1997，62（4）：1196－1207

［6］Phillip W S，House L S.Micro－seismic mapping of a Cotton Valley Hydraulic Fracture using decimated downhole arrays［J］.International Exposition and Sixty Eighth Annual Meeting，1998，9：13－18

［7］Dumay J，Fournier F.Multivariate statistical analyses applied to seismic facies recognition［J］.Geophysics，1988，53（9）：1151－1159

［8］De Meersman K，Kendall J M，van der Baan M.The 1998 Valhall microseismic data set：an integrated study of relocated sources，seismic multiplets，and Swave splitting［J］.Geophysics，2009，74（6）：183－195

［9］詹海刚，施平，陈楚群.基于贝叶斯反演理论的海水固有光学特性准分析算法［J］.科学通报，2006，51（2）：204－210 Zhan H G，Shi P，Chen C Q.Based on Bayesian inversion theory of inherent optical properties of seawater anaysis algorithm［J］.Chinese Science Bulletion，2006，512（2）：204－210

［10］王华忠，方正茂，徐兆涛，等.地震波旅行时计算［J］.石油地球物理勘探，1999，34（2）：155－163 Wang H Z，Fang Z M，Xu Z T，et al.Computation of seismic travel time［J］.Oil Geophysical Prospecting，1999，34（2）：155－163

［11］万永革，李鸿吉.遗传算法在确定震源位置中的应用［J］.地震地磁观测与研究，1995，16（6）：1－7 Wan Y G，Li H J.The preliminary study on the seismic hypocenter location using genetic algorithms［J］.Seismological and Geomagnetic Observation and Research，1995，16（6）：1－7

［12］屈永华，王锦地，刘素红，等.贝叶斯网络支持的地表参数混合反演模式研究［J］.遥感学报，2006，10（1）：6－13 Qu Y H，Wang J D，Liu S H，et al.Study on hybrid inversion scheme under Bayesian network［J］.Journal of Remote Sensing，2006，10（1）：6－13

［13］宋维琪，刘军，陈伟.改进射线追踪算法的微震源反演［J］.物探与化探，2008，32（3）：275－277 Song W Q，Liu J，Chen W.Microearthquake source inversion of an improved ray tracing algorithm［J］.Geophysical and Geochemical Exploration，2008，32（3）：275－277