铝蜂窝芯铝芯材成形过程仿真与实验研究

文义平，龙建军

（广东工业大学 机电工程学院，广东 广州 510006）

1 引言

铝蜂窝夹芯板是一种由两层薄蒙皮材料，中间粘结一层铝蜂窝夹芯构成的复合板，在航空航天、建筑、船舶、汽车等领域具有广泛的应用前景。目前粘胶铝蜂窝芯的工艺流程为：铝条涂胶，再多层叠装，切条，最后拉伸形成蜂窝状。但是这种工艺制备的铝蜂窝芯存在节点热强度不足的问题，同时由于铝蜂窝芯采用拉伸成型的方法，拉伸不均匀，存在格子规整性、平整性差的问题，难以在一些要求的工业领域应用。超声波焊接法是利用铝箔成型设备制备出三等边波纹铝箔切条，然后利用超声波携带高能量的特点焊接铝箔切条，直接成型为铝蜂窝芯。制备的铝蜂窝芯具有节点热强度高，蜂窝芯直接成型、不需再经过拉伸过程，所以不存在格子规整性、平整性方面的问题。

利用超声波焊接法制备铝蜂窝芯，需要有已经成形好的三等边波纹铝箔切条。目前国内外的许多学者在波纹铝箔成形方面开展理论与应用的研究。其中文献[1]研究了同步带成形半蜂窝薄铝板的机理及设备研究，文献[2]研究了基于LS-DYNA的半蜂窝芯材成型过程仿真与分析，一些科研人员[3]研究成形法制备半蜂窝波形条的有限元模拟，但以上的研究都只是关于力学分析及虚拟样机仿真试验，而未能在具体齿轮轴辊参数设计及校核精度等方面做进一步的研究。

采用齿轮式轴辊滚压成形法制备波纹铝箔，成形的铝箔结构均匀、误差小、能满足焊接工艺要求。参考文献[4-6]提出的蜂窝结构力学模型，利用刚粘塑性有限元法建立有限元模型，对铝蜂窝成形的工艺进行仿真计算，理论数值与实际试验相吻合。并在仿真的基础上对实验设备进行进一步的优化，论文的结果对齿轮式轴辊的设计具有参考作用。

2 波纹铝箔成形工艺研究及齿轮式轴辊的设计

2.1 蜂窝芯条成形工艺的研究

在采用齿轮式轴辊滚压成形制备波纹铝箔，在进料过程中，由于厚度为0.1mm 薄铝箔会受到自身重力而弯折，需要两组轴辊分别对铝箔进行张紧与压平。其制备工艺流程为：第一组为胶辊，其作用为增加轴辊与铝箔之间摩擦力，带动铝箔向前移动，第二组轴辊表面镀一层硬铬，其作用能将卷起的铝箔压平；，经过齿轮式轴辊滚压成形为波纹铝箔。成形工艺流程原理，如图1 所示。

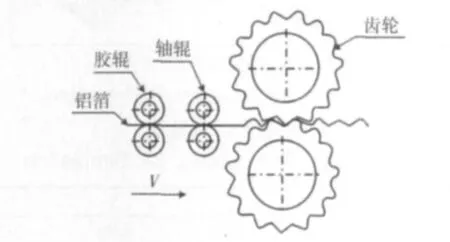
图1 波纹铝箔成形工艺流程原理图Fig.1 Forming Process of Half Honeycomb and Waveform Aluminum Sheet

2.2 齿轮式轴辊齿形参数设计

针对滚压弯曲成形后得到波纹铝箔是否与设计参数相符合，其主要设计参数为：边长a，齿顶角，厚度t，铝箔成形原理，如图2 所示。波纹铝箔参数，如图3 所示。在该试验中，a=5mm，θ=120°。对于波纹铝箔，要保证三个边长与相邻两角相等就可以保证不会出现成形的波纹铝箔挠曲或者间隙过大的现象。而波纹铝箔齿顶角的过大或过小与齿轮式轴辊的齿形角参数有关。

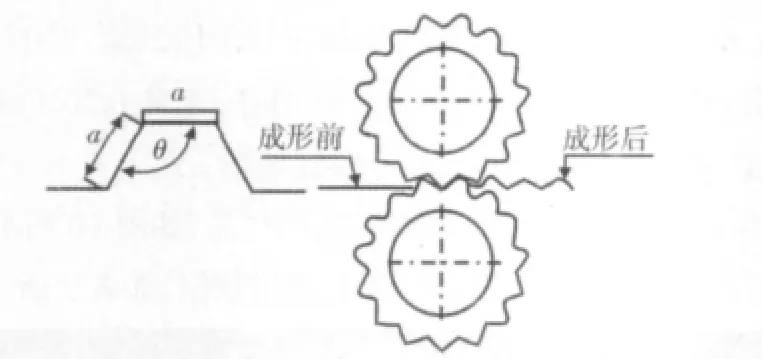
图2 波纹铝箔成形原理图Fig.2 Forming Half Honeycomb and Waveform Aluminum Sheet

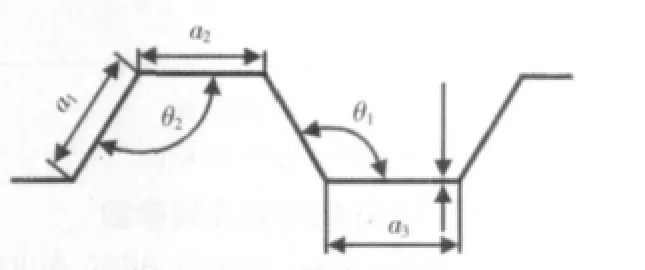
图3 波纹铝箔参数图Fig.3 Parameters of Half Honeycomb and Waveform Aluminum Sheet

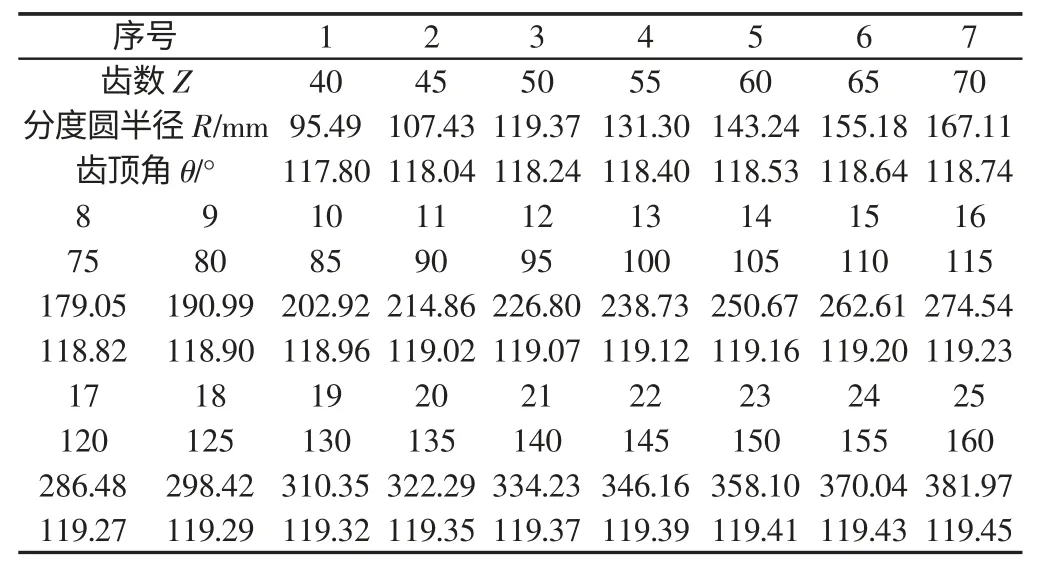
表1 仿真数据Tab.1 Simulation Data

现以边长a=5mm、齿顶角θ=120°、厚度为t=0.1mm 为波纹铝箔为例进行齿形角设计，由于铝箔滚压成形的过程并不完全是材料的塑性变形过程，其弯曲部分还存在着弹性变形，铝箔从齿轮式成形轴辊中取出后，弹性变形的恢复使铝箔的弯角发生了变化，成形后铝箔的形状与齿轮式成形轴辊的形状并不完全一致，存在回弹。而回弹的大小主要以回弹角度为表现形式。因此需要对齿顶角进行补偿与校正，由于齿顶角随着分度圆半径大小而的变化，它们之间存在一定的函数关系。用数学仿真的方法，以齿轮式轴辊的齿数线性递增取25 组数据，其数据，如表1 所示。

以分度圆半径R 为自变量，齿顶角θ 因变量，运用matlab 里面多项式曲线拟合函数polyfit 进行拟合[7]，得到它们之间的函数关系式及拟合曲线，如图4 所示。

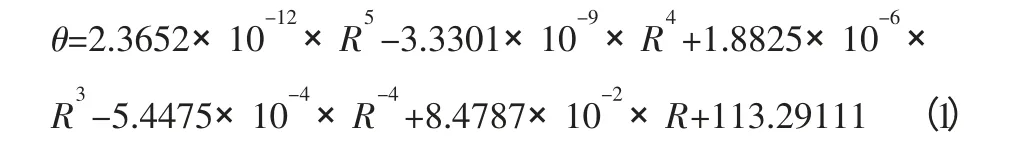
而分度圆半径R 与齿数Z 函数关系：

回弹角度△θ 为：

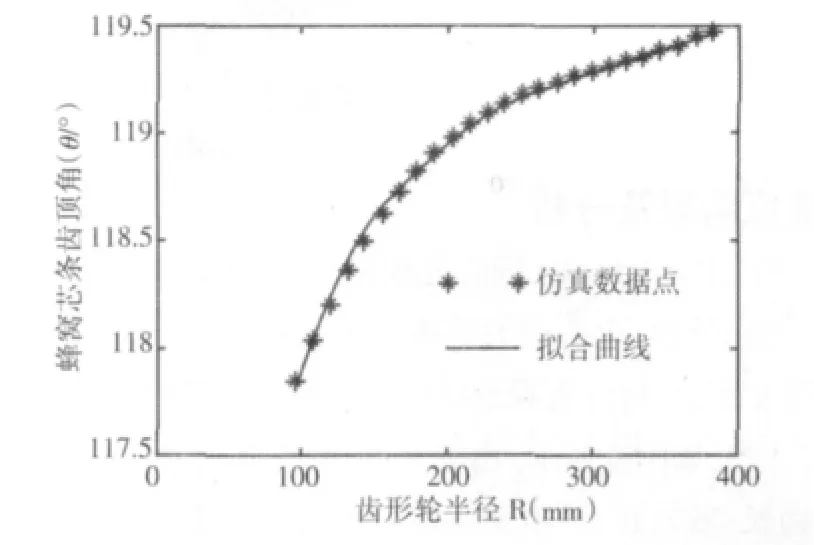
图4 拟合曲线图Fig.4 Fitting Curve

由以上回弹角、齿顶角及分度圆半径之间函数关系式可知，回弹角的大小与分度圆半径存在一定函数关系。分度圆半径过小，回弹角度变大，影响波纹铝箔成形的质量，而半径过大，回弹角度会变小，但是齿轮式轴辊的质量过大对整个成形设备的强度与刚度影响较大。由拟合曲线规律可以得到齿轮式轴辊参数选择为齿数Z=90、R=214.86mm、θ=119.02°，既能满足波纹成形质量又不影响整个成形设备的强度与刚度，所以比较适合。

对于不同的边长a，齿顶角θ 与分度圆半径R 函数关系不同，但是可以用类似的方法得到它们之间的函数关系式。

3 波纹铝箔成形过程仿真

用三维软件SolidWorks 建立凸模、凹模、铝箔三维模型，装配定位好并另存为STL 文件导入到DEFORM-3D 软件中[8]。

3.1 仿真模型的建立

图5 铝箔网格划分Fig.5 Meshing Aluminum Sheet

铝箔厚度为0.1mm，采用相对网格进行划分，网格划分过大其仿真出来的结果会发生畸变且误差较大；网格划分过密仿真过程比较繁琐且结果易失真。经过理论计算及仿真试验得出采用绝对网格划分的方式较好，其网格图，如图5 所示。其中铝箔定义为弹塑性体，凸模、凹模定义为刚性体，不需要进行网格划分和材料定义。在实际的试验当中，一对直齿齿轮式轴辊与铝箔的相对运动关系较复杂。为了便于滚压过程成形模拟过程的计算和结果准确性，我们从中任意取一对相互啮合齿，将其弯曲滚压过程等价转化为冲压过程，并在建立有限元模型时采用相对运动方式，即：假定凹模固定不动，凸模沿-Z 方向匀速运动，铝箔一端速度为零，另一端沿Y 方向运动，同时X 方向速度为0。设置凸模与铝箔及凹模与铝箔之间的关系，其摩擦因数为0.4。这样模拟与实际滚压成形的过程是等价的，其有限元模型，如图6 所示。

图6 有限元分析模型Fig.6 Model for Finite Element Analysis

3.2 模拟结果及分析

应用DEFORM-3D的后处理程序DEFORM-3D Post 对仿真结果进行后处理，得到应力等值云图，如图7 所示。应变等值云图，如图8 所示。可以直观地反应薄铝箔的变形情况。冲压成形后边界尺寸图，如图9 所示。由图9 可知，任意测量出三条边数据如下：侧边长、底边长，并由余弦定理可以得出相对应齿顶角，数据如表2 所示。

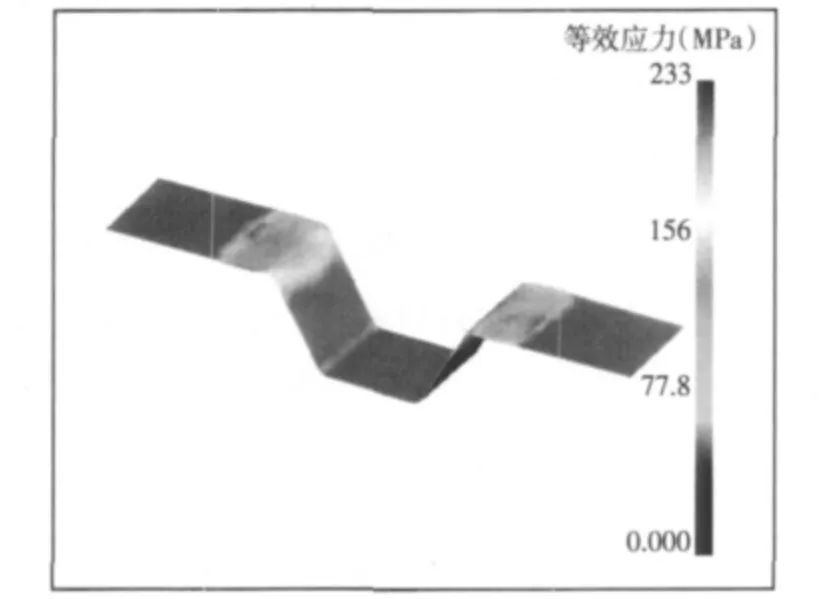
图7 冲压成型后等效应力图Fig.7 Equivalent Stresses after Mold-Stamping

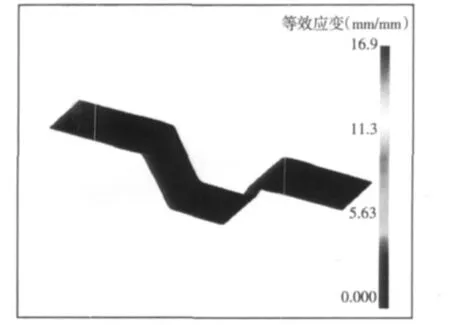
图8 冲压成型后等效应变图Fig.8 Equivalent Strains after Mold-Stamping

图9 冲压成形后边界尺寸图Fig.9 Dimension Drawings after Mold-Stamping

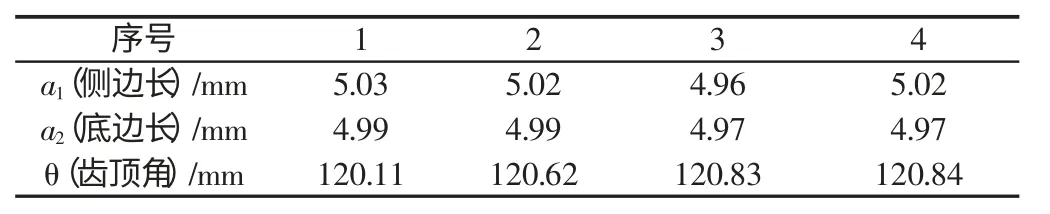
表2 成形仿真数据Tab.2 Forming Parameters for Simulation

齿顶角θ的平均值为：

理论值得相对误差为：

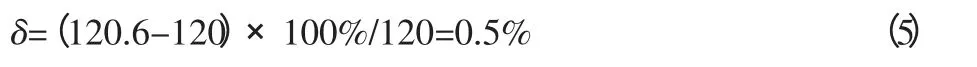
由仿真得到的结果，齿轮式轴辊参数的选用是合乎要求。

4 波纹铝箔滚压试验

试验利用大小相同的一对直齿齿形辊，对长600mm、宽50mm，厚0.1mm的3003 铝合金板进行滚压试验。3003 铝合金主要成分（质量分数，%）为Si≤0.20，Mn1.20，Mg0.20，Cu0.20，Zn≤1.50，Al 余量，延展性能好，易于塑性成形。

作波纹成形滚压试验，得到成形产品，如图10 所示。并取有代表性的一段成形波纹铝箔，相关测量数据，如表3 所示。

图10 试验结果Fig.10 Test Results

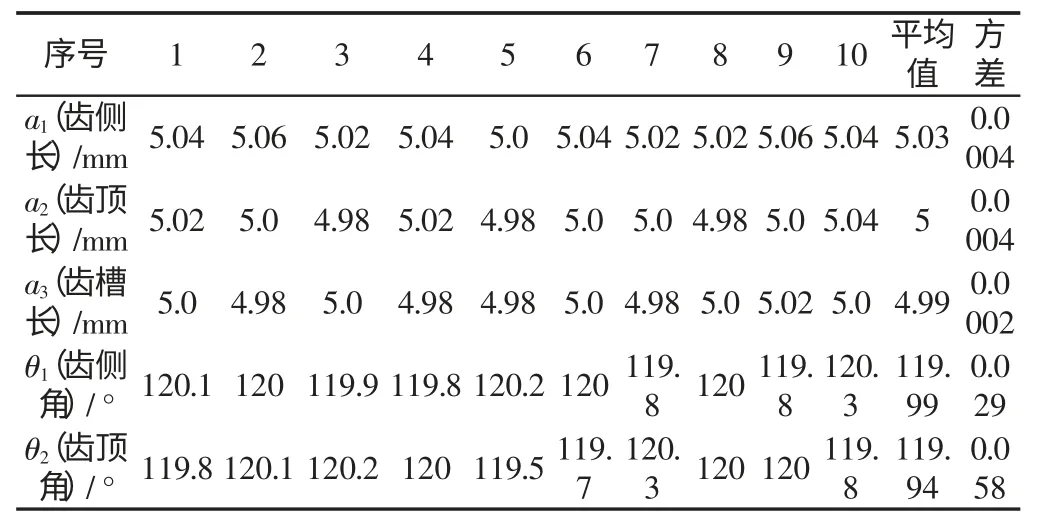
表3 铝箔成形后几何参数Tab.3 Geometric Parameters after Aluminum Sheet Mold-Stamping

由以上得到各平均值及方差可知，试验得到的波纹铝箔产品与理论设计及仿真结果的相当吻合。

5 成形结果讨论与分析

通过比较有限元分析结果与实际试验结果，可以得出影响波纹铝箔成形的因素有很多，比如齿轮式轴辊的装配误差、成型辊的转速与薄铝板进料速度等因素。在做滚压成形试验时，互相啮合齿轮式轴辊不在同一个平面，相互之间错开一定角度，得到的波纹铝箔就不规则，误差很大。在试验之前，应当调整好轴辊中心距且调平。

6 结论

通过应用DEFORM－3D 有限元分析软件对成形法波纹铝箔的过程仿真，并与试验得到的波纹铝箔进行数据比较，得知通过金属塑性成形仿真来预测连续弯曲滚压成形结果有效，这为齿轮式轴辊辊滚压成形波纹铝箔提供重要的理论分析模型。

同时成形方式，铝箔－齿轮式轴辊的速度关系及装配误差对成形的结果有很大影响。

齿轮式轴辊的参数设计及回弹角度的补偿对整个成形起着关键作用，所以得出它们之间函数关系式非常必要。

［1］刘荣，刘泓并，贾旭鹏.同步带成形半蜂窝薄铝板的机理及设备研究［J］.机械设计与制造，2007（1）：85－87.（Liu Rong，Liu Hong－bin，Jia Xu－pe.The mechanism and equipment research in forming half honeycomb sheet with ambulacrum［J］.Machinery Design＆Manufacture，2007（1）;85－87.）

［2］王飞，蒋志涛，冯玲兵.基于LS－DYNA的半蜂窝芯材成型过程仿真与分析［J］.科技导报.2008，26（13）：49－51.（Wang Fei，Liu Hong－bin，Jiang Zhi－tao，Feng Ling－bing.Forming Process Simulation of Half－honeycomb Profile Strip Based on LS－DYNA［J］.Review Science and Technology，2008，26（13）：49－51.）

［3］贾旭鹏，刘泓滨，刘荣.成形法制备半蜂窝波形条的有限元模拟［J］.机械设计与制造，2007（3）：95－97.（Jia Xu－peng，Liu Hong－bin，Liu Rong，Huang Ya－yu，Sun Yong.Thefinite element simulation of the form based half honeycomb profile strip［J］.Machinery Design＆Manufacture，2007（3）：95－97.）

［4］关键，朱宗文，宋霖，等.蜂窝夹心板频响特性的研究［J］.四川大学学报：工程科学版.2004，36（3）：69－72.（Guan Jian，Zhu Zong－wen，Song Lin，etc.Frequency Response of Honeycomb Sandwich Panels.Journal of Sichuan University（Engineering Science Edition），2004，36（3）：69－72.）

［5］张铁亮，丁运亮，金海波.蜂窝夹层板结构等效模型比较分析［J］.应用力学学报.2011，28（3）：275－282+327.（Zhang Tie－liang，Ding Yun－liang，Jin Hai－bo.Comparative analysis of equivalent models for honeycomb sandwich plates［J］.Chinese Journal of Applied Mechanics，2011，28（3）：275－282+327.）

［6］夏利娟，金咸定，汪庠宝.卫星结构蜂窝夹层板的等效计算［J］.上海交通大学学报，2003，37（7）：36－38.（Xia Li－juan，Jin Xian－ding，Wang Yang－bao.Equivalent Analysis of Honeycomb Sandwich Plates for Satelite Structure［J］.Journal of Shanghai Jiaotong University，2003，37（7）：36－38.）

［7］郭仁生.机械工程设计分析何MATLAB 应用［M］.北京：机械工业出版社，2008.（Guo Reng－sheng，etal.Mechanical engineering design ＆ analysis and MATLAB Application［M］.Beijing：China Machine Press，2008.）

［8］李传民，王向丽.金属成形有限元分析实例指导教程［M］.北京：机械工业出版社，2008.（Li Chuan－min.Wang Xiang－li.Finite Element Analysis Instance Tutorials of Metal Forming［M］.Beijing：China Machine Press，2008.）