城市交通干线双向绿波带控制技术研究

朱和 常玉林

（江苏大学汽车与交通学院 江苏 镇江 212013）

0 引言

城市主干线承受着巨大的市内交通负荷，提高主干线的双向协调控制效果，降低主干线上的车流的延误时间和停车率，对改善整个城市交通状况具有重大的实际意义。干线协调控制是干道的交通管理与控制的1种主要策略，就是将干道上的一连串信号交叉口按一定方式联结起来作为系统对象研究，同时对各个交叉口进行配时方案设计以保证互相协调，从而使得主干道上行驶的车辆可以获得尽可能少的停车率或较少的行车延误。

目前干线协调控制方法虽多种多样，但总体分3类：定时协调控制、感应协调控制和自适应协调控制［1］。定时协调控制指干线交叉口信号按预先设定的方案运行。如Little 提出最大带宽MaxBand控制策略，Gartner等人在MaxBand方法的基础上提出复合带宽MultiBand 控制策略［2］。感应协调控制是根据交通量的变化而变化的1种控制方式，其中交通量可由埋设在干道上的感应线圈获得。其设计思想主要有2种：①根据监测到的交通量，实时计算出最佳的控制方案；②根据检测到的交通量，从预先设定的配时方案中，选择合适的控制方案。感应协调控制可以满足实时交通需求，但在实际运行中，感应协调控制一般只适用交通量较小的干线，在接近饱和状态的交叉口，感应控制方式的效果未必有定时协调控制的效果好。自适应协调控制能够连续测量交通流状态，逐步了解和掌握对象，实时调控保证控制效果达到最优。典型的自适应控制系统有：SCATS、SCOOT、RHODE系统［3］。

干道协调控制设计主要原则有［4］：绿波带最大化；交通性能最小化。基于绿波带最大化的设计方法是主要通过追求绿波通行时间与公共信号周期比值的最大化，即以车辆连续通过带宽作为评价指标来研究干线配时方案的协调控制效果，从而确定控制系统中各交叉口的信号配时参数值，常用算法有数解法、图解法等；基于交通性能最小化的设计方法则是依据干道协调控制系统的延误时间和停车次数与信号配时参数之间的对应关系，利用优化算法寻找最佳的路径以确定各交叉口配时参数，从而实现干道协调控制系统的总延误最小，常用算法有蚁群算法、遗传算法等。

城市干线双向协调控制是干道交通协调控制中应用最为广泛的1种控制手段，该方式有以下优点：①交通流更平滑稳定，能够提高道路交通服务能力与通行能力；②保证整体车流以较高的行驶速度和较低的延误率；③行驶车速更加协调统一，保证车辆尽量不停顿通过下一路口；④可以吸引附近车辆进入主干线，使局部路网更加协调通畅；⑤行人和驾驶员都更加遵守交通规则，紧凑的交通流可减少行人违规穿越马路，避免交通事故。

本文采用是定时双向绿波协调控制策略，在现有的MaxBand核心模型的基础上，以双向绿波带宽和最大为目标，引入启动清空时间即车辆连续通过干道在各交叉口停车时启动时刻到通过停车线时刻的时间差。利用数学软件和绘图工具获得更符合实际的相位差，保证绿波带宽度和它的实际有效性。同时采用多时段多区段方针，保证交通干线各交叉口有效协调控制，实现全天候双向有效绿波带。常州市武进区常武路的实际应用证明了该控制策略方案的有效性和实用性。

1 问题描述

双向绿波带协调控制的目标是保证干线双向交通通畅，使进入该干线的车辆一路绿灯行驶，且双向车流拥有较宽的通过带。大量的实践应用表明：当相邻2交叉口之间的距离超过800m 时，协调控制效果反而不如干线上交叉口的单点控制，但在交通过饱和的情况下，距离太近也不利于协调控制。双向绿波带需优化设计的主要参数是：信号公共周期、绿信比和相位差。为使干线上各交叉口的交通信号控制能取得协调，各交叉口的信号周期长度必须相同。为此，首先按单个交叉口信号控制的配时方法，计算各交叉口周期时间长度，然后从中选出最大的周期长度作为这个系统的公共周期，获得最大周期的交叉口称关键交叉口［5］。在双向协调控制系统中，很明显相位差的准确性直接决定着绿波带的实际效果。相位差分为绝对相位差与相对相位差，绝对相位差是指干线系统中把某一路口作为基准路口，其他路口的协调相位起始时刻滞后于基准路口的协调相位起始时刻的最小时间差，相对相位差是指干线系统中任意两相邻信号绿灯或红灯的起点或终点的最小时间之差。模型中一般采用相对相位差，其值与相邻交叉口间路段长度和车辆在该路段间的行驶速度有关。且控制方案应该与1d的交通流实际状况相协调，特殊的时段分配不同的优化配时方案，否则方案不满足现状，可能造成交通流的集结，引起交通絮流，产生进一步的交通堵塞。

2 双向协调绿波设计

2.1 双向绿波协调控制的基本原理

协调控制是对城市交通干线或某区域的多个平面交叉口作为系统进行整体控制，且控制方案相互协调，使得进入干线的车流按某一速度行驶时，能不遇或少遇红灯，车辆通过该干线或该区域内时，保证绿波带最宽、停车次数最少、延误时间最短等。

干线协调控制方法中最大绿波带法是以车辆连续通过带宽作为评价指标，建立混合整数线性规划模型，通过最大化绿波带与公共周期的比值来获得相位差。目前基于绿波带宽最大化的设计有两类方案：不变带宽绿波和可变带宽绿波。所谓不变带宽绿波是指双向的绿波带宽大小是不变的，可变带宽绿波是指在不同路段、不同方向实施不同连续带宽模型。不变带宽模型的致命缺陷是不能根据实际交通的变化实时调整带宽，满足实时需求。可变带宽绿波不仅能变动路段间的绿波宽度，还能给两向车流分配不同带宽。由于可变带宽绿波方法涉及到的较多参数求解，计算量大，不能快速得到最优解，但实际效果明显优越不变带宽。

2.2 改进的双向绿波带宽优化模型

MaxBand核心数学模型为Little研究的混合整数线性规划算法［6］，能得到各个交叉口信号相位差、绿信比、周期和最佳左转行车信号。本文在该模型中引入启动清空时间参数qm，i和q′m，i，其取值大小随干线交通实际情况而定。本文通过大量连续来回跟车调查，统计车辆到各交叉口停车时启动时刻到通过停车线时刻的时间差，统计取其平均值qi和q′i，同时大量数据统计发现，车辆通过这条干线时，在某些交叉口停车次数频繁，但在某些交叉口无需停车或停车次数很少且时间短，本文规定启动清空时间为零。如果不考虑行驶启动清空时间，停车延误必然会更影响绿波带的实际效果，达不到预期的目标。修改模型为

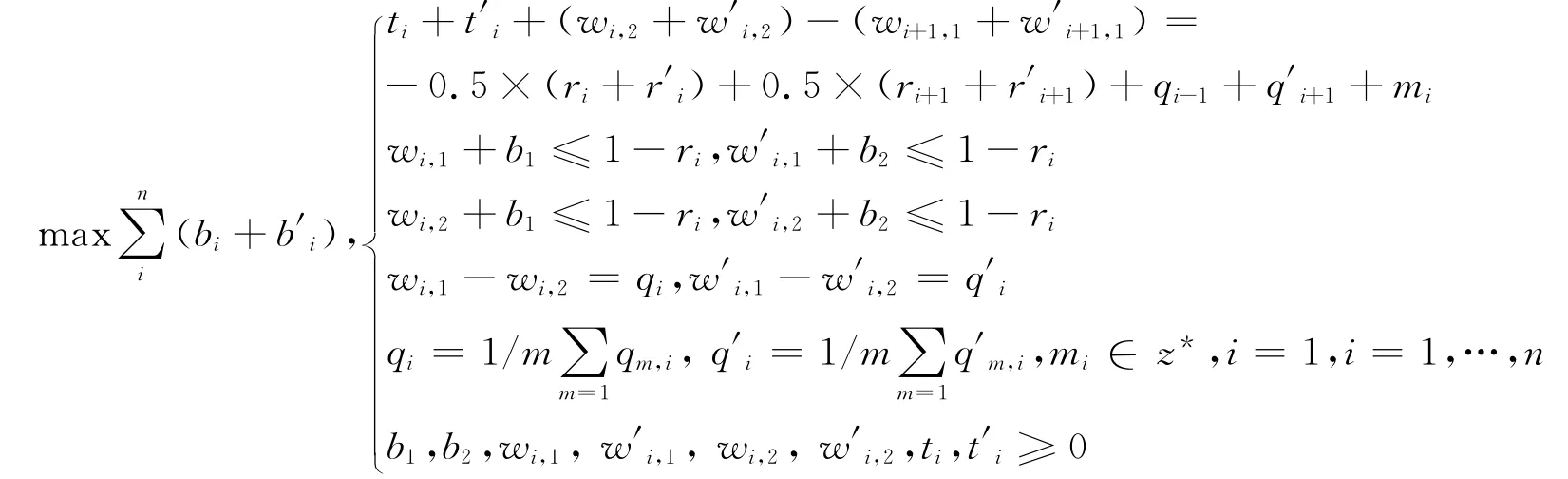
模型中：bi（b′i）为交叉口与交叉口间两方向的绿波带宽度；ri为路口Ii的红灯时间；ti为从交叉口Ii到交叉口Ii＋1的行程时间，等于t′i；wi，1（w′i，1）为交叉口Ii下端绿波带边缘和其左（右）侧相近红灯的右（左）侧边缘间的时间差；wi，2（w′i，2）为交叉口Ii上端绿波带边缘和其左（右）侧相近红灯的右（左）侧边缘间的时间差；qm，i（q′m，i）表示第m 次i 交叉口两方向的启动清空时间；n表示干线系统中有绿灯控制交叉口个数。模型中交叉口之间的几何关系见图1。

图1 交叉口之间的几何关系Fig.1 The geometric relationshipbetween the intersections

利用LinGo软件计算该优化模型，算法数据输入：公共周期、绿信比、交叉口间距和路段行驶时间；输出：上下行带宽、影响因子、迭代次数。

3 实例验证与分析

常武路是常州市武进区南北向的主要通道，它的交通畅通，对于缓解市区交通拥堵和改善武进区形象具有举足轻重的作用。该交通干线南北方向道路为承担较重负担的主干线，东西方向道路为支路。现状道路规模为机动车双向6车道，道路两侧还设有2条公交专用车道。常武路从与聚湖路交叉口至与延政路交叉口之间全长约4.2 km，共有11个信号交叉口。常武路沿线交叉口间距在250～650 m 之间，交叉口间距相差不明显。常武路的交通状况非常适合采用双向绿波带协调控制。

系统优化前，常武路各路口主要采用简单的单路口多相位多时段定时控制方式，建立之初为武进区的发展做出很大贡献。但是，随着社会经济的发展和车辆数的剧增，这种控制方式已经不能满足人们日益增长的交通需求。而且，常武路交叉口的交通信号“各自为政”的单点控制方式，给常州市造成巨大的经济损失和环境污染。所以有必要对常武路交通信号控制进行调整，以满足社会发展需要。

首先必须对绿波带速度进行取值，本项目取值主要来自道路车速调查。调查方式主要有测速仪测量和跟车调查。常武路同时选择了这两种方法。所测结果总体一致。小汽车平均速度为48.00km／h；中型车平均车速为44.56km／h；大型车平均车速为37.00km／h。车速主要分布在40～55km／h之间，占总量达到的70.4%。

根据常武路的特点，将绿波带速度设计分为3种情况，日平峰（09：00～16：30时）取50km／h，早晚高峰（07：00～09：00时／16：30～19：00时）取45km／h，早晚平峰（05：00～07：00 时／19：00～21：30时）和夜间（21：00～05：00时）取55km／h。另外，平峰时段，常武路南北方向车流分布较均匀，而在高峰时段常武路南北车流分布较悬殊，交通流呈明显的潮汐现象，在早高峰时段，由北向南车流明显大于对向，而在晚高峰时段，由南向北车流量较大。因此在设计双向绿波控制时，早高峰期间由北向南优先保证绿波带最优，晚高峰期间由南向北优先保证绿波带最优。

根据路口间距、相交道路性质及交通状况将常武路从北至南11个交路口分为4个区间。第一区间：聚湖路、东方路交叉口；第二区间：人民路、古方路、定安路交叉口；第三区间：广电路、长安路交叉口；第四区间：虹北路、长虹路、府西路、延政路交叉口。通过多次来回跟车调查，统计计算启动清空时间与停车次数，以早高峰为例，见图2、3。

从图中看出，早高峰期间北向南方向需停车的交叉口比较多，而南向北需停车的交叉口比较集中且次数较少，主要原因是与该区域的交通潮汐现象和交叉口周围的环境密切相关。模型计算结果利用CAD 绘制时距图，相位差可从图中直接测量获得。

图2 北向南方向启动清空时间与停车次数平均值Fig.2 The average value of starting empty time and parking times from north to south

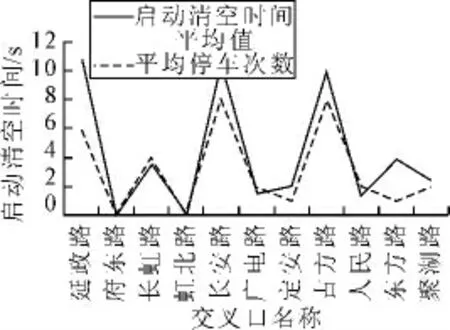
图3 南向北方向启动清空时间与停车次数平均值Fig.3 The average value of starting empty time and parking times from south to north

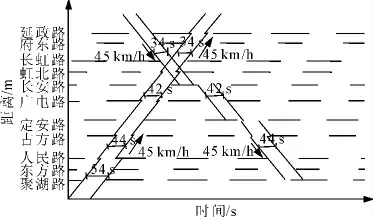
图4 早高峰双向绿波的效果图Fig.4 The functional drawing of the morning peak

从图中看出绿波带宽度保持在34～54s范围内。理想情况下，北向南方向机动车通过该干线最多停车1次，而反向效果稍差，主要考虑早高峰期间由北向南车流量较大，优先保证该方向绿波带宽度和低停车率。

4 系统设计仿真评价

为了验证优化方案的有效性，利用德国PTV公司的微观交通仿真软件Vissim 进行仿真，首先建立与实际相符路网模型，然后输入交通流量，周期，相位差等相关参数，选取合适的位置设置相应的评价参数检测器，并针对不同时段的配时方案仿真。对优化前后进行了对比实验，比较了绿波带优化对平均停车次数、平均延误、平均行驶时间的影响。如早高峰效果对比见表1，测试数据结果表明该双向绿波带控制策略可以有效改善干线交通阻塞状况，而且效果十分明显。同时实际跟车调查发现道路行驶速度明显提高，实验结果符合交通需求。

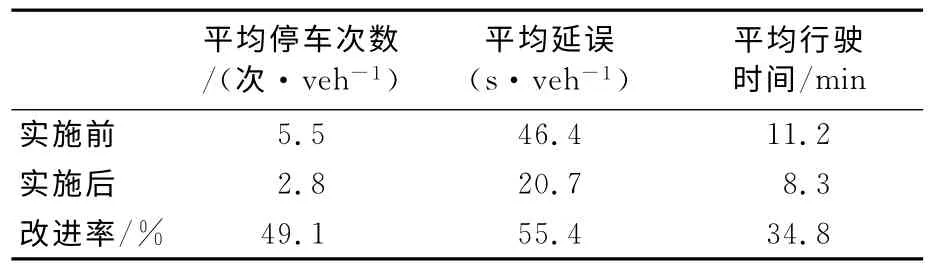
表1 实际使用效果对比Tab.1 The comparison of the practical effects

5 结束语

本文提出1种适用于中小城市干线交通信号双向绿波的定时协调控制策略，这种控制方案高效率、低成本而且实施简单，适用价值高。这种控制策略的关键点在于相位差获取。首先对干线现状调查分析、计算周期和绿信比等，再通过跟车调查引入启动清空时间，建立混合整数线性规划模型，获得更符合实际的干线相对相位差以及其它相关参数。实例验证了此种控制策略的现实意义。但交通流处在不断变化中，对控制的关键点处理方法需继续观察改进，特别是横向干扰影响车流带速的处理问题还未得到妥善解决。

［1］张飞舟，范耀祖.交通控制工程［M］.北京：中国铁道出社，2005.

［2］李 林，徐建闽.干道交通协调控制的MILP 改进算法［J］.公路交通科技，2009，26（S1）：93－96.

［3］沈国江，许卫明.交通干线动态双向绿波带控制技术研究［J］.浙江大学学报，2008，42（9）：1625－1630.

［4］郑翔骥，陈明凯.一种实现双向绿波信号控制的方法［J］.交通与计算机，2004，22（5）：46－48.

［5］张昌禄，翟润平.交通干线信号协调控制方法综述［J］.中国人民公安大学学报，2007（1）：87－90.

［6］Little J D C.The synchronization of traffic signals by mixed－integer linear programming［J］.Operations Research，1996（14）：568－594.