加固双曲拱桥时变可靠度研究

王 楠，刘 洋

（中交武汉港湾工程设计研究院有限公司，武汉 430070）

一般来说，双曲拱桥是由多个预制构件拼装组成，施工方便，外形美观，经常作为公路桥梁遍布各地。但在后期的运营过程中，大多数双曲拱桥出现构件结合面开裂的现象，目前已很少使用。对出现病害的双曲拱桥通过修复加固措施来提高承载力，可以有效的减少经济投入，符合社会发展的需要。依据可靠度的原理，对加固后的双曲拱桥进行研究，既可以检验加固效果，又可以分析出运营后期桥梁使用情况。

我国的可靠度研究起步较晚，但发展速度很快，取得了不少结论性的研究成果。文献［1］研究了多种腐蚀因素（混凝土碳化引起的钢筋腐蚀、氯离子侵蚀引起的钢筋锈蚀及硫酸盐和硫酸溶液引起的混凝土腐蚀等）作用下混凝土构件的可靠度分析方法。文献［2］改进了方向抽样法，使Monte－Cole法的计算精度更高。文献［3］运用可靠度理论，分析了既有结构的剩余寿命，对结构后期的运营有较强的指导意义，为交通运输管理部门作出正确决定提供参考。文献［4］将模糊数学的方法引入可靠度中，分析了CFRP 加固后的混凝土梁的可靠度指标，该研究提高了可靠度计算的精度，对实际工程具有指导意义。该文根据实测的混凝土强度值，利用时变可靠度理论，综合考虑抗力衰退、荷载随机变化等因素，分析了采用增大截面法加固的双曲拱桥的可靠度及剩余使用寿命。

1 时变可靠度分析

1.1 时变可靠度的基本理论

桥梁结构的时变可靠度定义［5］：在规定的继续使用期内，在正常使用、正常维护条件下，考虑环境和结构抗力衰减等因素的影响，在任意时刻完成预定功能的概率，即Ps（t）∈［tτ，Ts］，可用公式（1）表示。

其中

式中，tτ为桥梁结构服役分析时刻；Ts为设计基准期；Z（t）为考虑桥梁结构tτ时刻的功能函数；R（t）为考虑tτ时刻桥梁结构；S（t）为考虑tτ时桥梁结构荷载效应。

1.2 加固后结构的时变可靠度计算

随着时间的推移，结构的使用性能不断发生着变化，构件会出现老化和损伤现象。因此，结构的抗力计算，要综合考虑多种因素的作用，其中，主要有荷载效应因素、使用环境因素和材料因素。其抗力衰减表达式为

式中，Kp为描述计算模式不确定性的随机变量；R（·）为由材料参数和几何参数计算得到的抗力随机过程。

对于加固后的结构，可以按照一般既有结构时变可靠度分析方法得到。文献［6－7］通过调查分析得出混凝土强度和钢筋随时间变化的规律。根据研究需要，文中采用文献［10］将结构抗力的随机过程表示为

式中，R0为结构的初始抗力；（t）为一确定性的时间函数。

1.3 荷载模型

结构在运营过程中，要承受多种荷载效应，包括恒载、汽车荷载、行人荷载、风荷载和地震荷载等，若研究所有荷载作用下桥梁的内力变化对结构可靠度的影响既不科学又不实际。因此，根据该文工程实例的具体运营情况，在进行结构可靠性分析时只研究恒载和汽车荷载。

1.3.1 恒载

一般情况下，桥梁的恒载近似不变。但在桥梁运营的后期，由于各种病害的出现，需要进行维修和加固。采用增大截面法加固使原结构的截面发生了显著变化，结构的自重变化较大，其标准值与拟建结构有较大差异，应当在对桥梁加固后的实际尺寸进行详尽的实测统计分析后，重新求得构件自重统计参数，均值为uG＝1.104 8GD，变异系数为δG＝0.043 1。其中，GD为恒载设计值。

1.3.2 车辆荷载

桥梁加固后，在不考虑荷载等级提高的情况下，车辆荷载效应最大值分布依然服从极值I型。时段t内可变荷载效应的平均值和均方差为

式中，a＝π／（）；uQT，σQT分别为可变荷载的平均值和标准差；uQT0，σQT0分别为设计基准期T0内荷载效应极大值的平均值和标准差。

1.4 可靠度分析

1.4.1 基本假设

采用增大截面法加固混凝土构件时，一般会在老混凝土上植筋，再浇筑新混凝土，这种方法可以有效的结合新老混凝土，所以在该文的分析过程中，不考虑新老混凝土之间的变形协调问题。荷载效应主要考虑恒载和汽车荷载。

1.4.2 可靠度计算步骤

采用Midas／Civil对结构进行有限元分析，考虑抗弯失效模式。由于拱波、拱板对结构的弯矩贡献较小，故在建模中不对该部分进行模拟，其自重以体力的形式直接施加在立柱上。

1.4.3 一次二阶矩法

一次二阶矩法的基本原理是：首先将随机变量的非正态分布转化为正态分布，然后将功能函数用泰勒级数展开。

2 工程实例

2.1 工程概况

某双曲拱桥梁全长57m，桥面总宽8.33m，上部构造为L0＝40m 的双曲拱，净矢高f0＝5.71m，矢跨比f0／L0≈1／7，已服役33年。旧桥设计荷载等级为汽车－15级，挂－80。

本桥采用增大截面法加固，主要是在拱角至L0／4之间的拱背上浇筑不等厚的混凝土。在拱角处浇筑45cm 厚的混凝土，在L0／4处浇筑25cm 厚的混凝土，其间逐渐变化。新旧混凝土之间采用植筋的方法进行连接，如图1所示。该桥加固后的设计荷载为公路－Ⅱ级。

2.2 可靠度计算

根据检测数据（见表1），计算得到的混凝土强度值f＝10.36 MPa，建立有限元模型图如图2所示。计算分析表明拱脚为最不利截面，故取拱脚截面为控制截面。

考虑抗弯失效模式，计算拱脚的抗力及荷载统计参数，见表2。

桥梁在运营期间，汽车荷载效应的计算采用离散化的方法，离散时间为5年，按照式（5）、式（6）计算相应的统计参数，见表3。

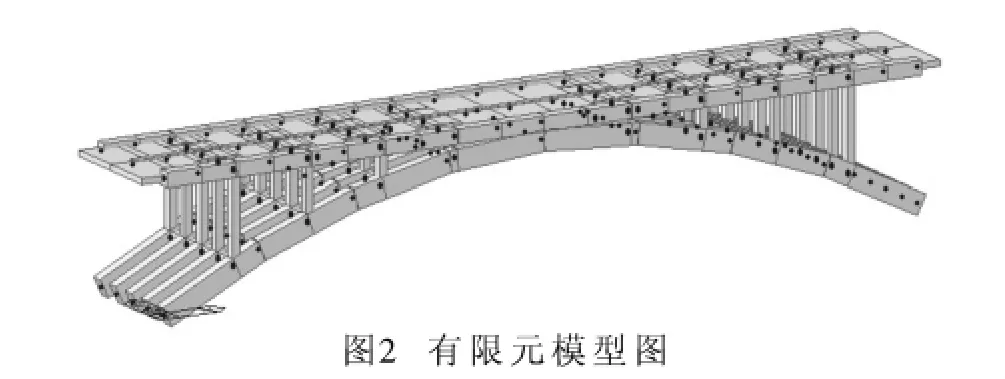
表1 实测混凝土强度值

表2 抗力及荷载统计参数

表3 车辆荷载统计参数

根据表3所示的各个使用阶段荷载统计参数，采用一次二阶矩法对构件进行可靠度计算，结果显示加固前的双曲拱桥可靠度指标为β＝3.52＜0.85β0＝3.57（β0 为设计基准期内的目标可靠度）。从结果可以看出，可靠度指标不满足要求，需要进行加固。采用拱背增大截面的方法进行加固后，该双曲拱桥的可靠度指标为β＝4.1，在后续服役60年内结构的可靠度均可以满足使用要求（如图3所示）。

4 结论

该文结合一拱背加固的双曲拱桥实例，分析各因素对加固后拱桥可靠度的影响，得到结论如下：

a.采用在拱背浇筑混凝土的方法在有效提高双曲拱桥抗力的同时，明显提高了结构的可靠度；

b.根据目标可靠度，利用结构可靠度指标与时间的对应关系，可以得出结构剩余使用寿命，为既有结构的加固改造提供合理的决策依据。

［1］仲伟秋，赵国藩.多种腐蚀因素作用下钢筋混泥土结构的可靠度分析［J］.土木工程学报，2001，36（11）：1－5.

［2］贡金鑫，何世钦，赵国藩.结构可靠度模拟的方向重要抽样法［J］.计算力学学报，2003，12（6）：655－661.

［3］赵尚传，赵国藩.基于可靠性的在役混凝土结构剩余使用寿命预测［J］.建筑科学，2001，17（5）：19－22.

［4］卢少微，谢怀勤.CFRP加固RC梁的模糊随机可靠度数值模拟［J］.应用力学学报，2009，26（1）：161－185.

［5］彭文韬，邓志勇.基于时变可靠的桥梁评估与剩余寿命预测.［J］武汉理工大学学报，95－97.

［6］赵尚传，赵国藩，贡金鑫.在役混凝土结构最优剩余使用寿命预测［J］.大连理工大学学报，2002，17（5）.

［7］Mori Y，Ellingwood R.Time－dependent System Reliability Analysis Adaptive Importance Sampling［J］.Structural Safety，1993，12（1）：59－73.

［8］贡金鑫，赵国藩.大气环境下锈蚀对钢筋混凝土结构可靠度的影响［J］.大连理工大学学报，2000，40（2）：210－213.