塔河碎屑岩注水井试井解释的一种新方法

万小勇，杨利萍，龙武

邹宁，陶碧娥 （中石化西北油田分公司工程技术研究院，新疆 乌鲁木齐 830011）

试井中测定的井筒压力是地层流体渗流的直接反映，它携带了地层流体以及储层特性的信息，其中必然也包括剩余油分布的信息。该研究建立起来了注水井单相多区复合油藏数学模型。通过典型曲线分析法或非线性自动拟合法获得地层渗透率、水驱前缘半径和剩余油饱和度分布等地层参数。

非线性自动拟合法也称为非线性回归法、自动典型曲线拟合法或自动试井分析，它与典型曲线分析法一样，一次可拟合所观测到的整个数据。这种方法不同于以往的图形辅助分析技术，它使用数学算法使观测的数据与选定的储层模型拟合。

非线性自动拟合法通过改变未知的储层参数使模型与测试数据充分地拟合，其参数估计是建立在最小二乘法的基础上，即使测试压力与模型压力差的平方和最小。

国内外试井专家提出的试井分析典型曲线的自动拟合法，大多数都是基于无约束最优化方法Newton法和Gauss－Newton 法。Newton 法由于需要计算二阶导数，费时较多，故使用较少；而Gauss－Newton法不需计算二阶导数，但对初值要求较高［1～4］。LMF（Levenberg－Marquardt－Fletcher）法综合了上述两类方法并加以改进，是当前求解无约束最优化问题和非线性最小二乘问题的最有效的方法之一［5，6］。

1 理论模型函数的计算

油藏注水后，由于油水黏度差、毛细管现象、岩层微观不均匀的影响，使得水渗入油区后，出现一个油水两相同时流动的两相区。随着注水时间的延长，两相区逐渐增大，注水井周围形成了高含水区域（或水淹区），沿井筒向外含水饱和度逐渐减小，在注水前缘以外是具有原始流体饱和度的油区，油藏内形成了流体的饱和度梯度。设一口注水井泄流半径re，水驱前缘半径rf，水淹半径rl，束缚油饱和度Sor，束缚水饱和度Swi，含水饱和度Sw，见图1。

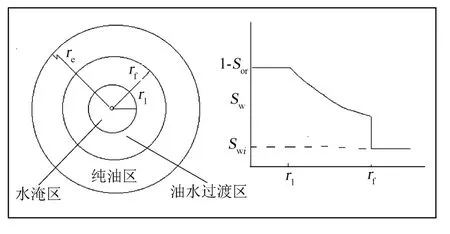
图1 注水油藏物理模型

为得到注水油藏不稳定压降解，首先将注水油藏划分为多区复合油藏：即油水两相区按等饱和度的原则进行剖分，将饱和度剖面离散为一系列同心圆环区域，每一离散区域有各自的总流度λt＝K（Krw／μw ＋Kro／μo）和综合压缩系数Ct＝（SwCw＋SoCo＋Cf），如图2所示。当复合油藏区间数N趋于无穷大时，多区复合油藏近似于存在饱和度和流度梯度的注水油藏系统。这种近似的实质是把两相流动的影响转化为地层的影响，用单相多区复合油藏来近似两相均质油藏。

为了应用注水井停注后所测的压降资料解释这个系统，求出多区复合油藏的单相注入解之后，考虑到关井测压过程中的流量变化，把多区复合油藏单相注入解进行迭加，可得到多区复合油藏关井时的不稳定压力解，即注水井关井后的不稳定压降响应解析解［7，8］。

假设油藏均质、等厚、各向同性，流体微可压缩，流体流动符合达西定律，流体在地层中的流动属等温流动，忽略重力和毛细管力的影响。多区复合油藏的无量纲形式的数学模型如下：

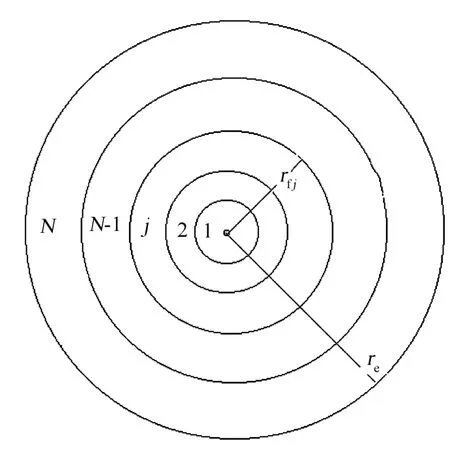
图2 多区复合油藏系统示意图

通过拉氏变换，将原实空间的偏微分方程组转变为拉氏空间常微分方程组，就可以得到多区复合油藏单相注入条件下井底不稳定压力（拉氏空间）解：

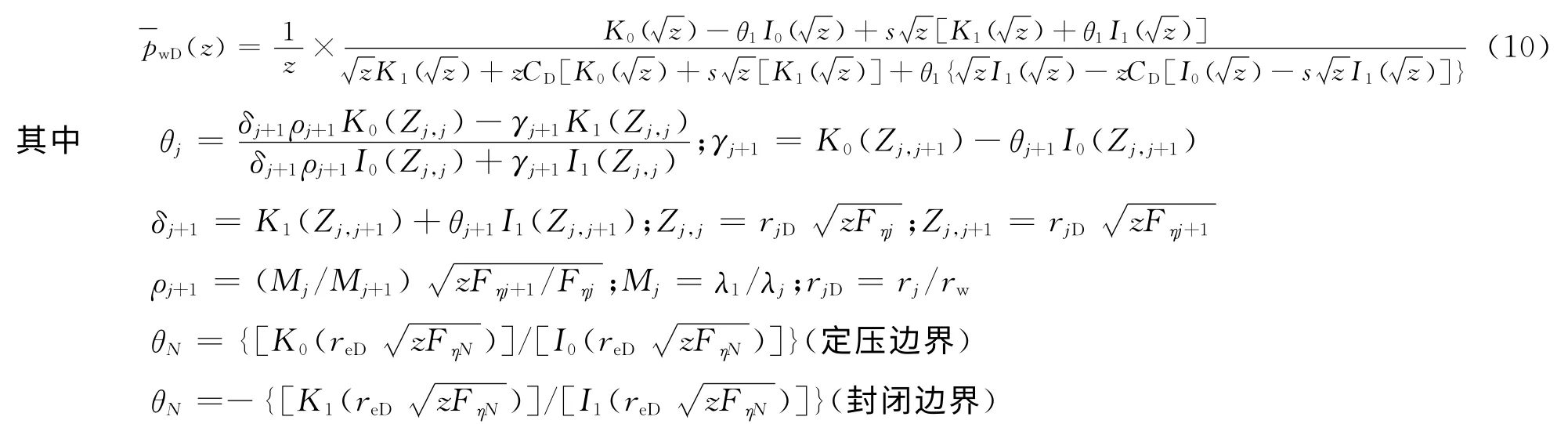
式中：pwD（z）井底压力拉氏空间解；z为拉氏变量；I0、I1第一类一阶和二阶变形Bessel函数；K0、K1第二类一阶和二阶变形Bessel函数。

对于拉氏空间解，如果采用解析方法反求实空间的解，那就十分复杂，且不便于计算机处理，试井分析中常采用Stehfest数值反演方法。应用Stehfest数值反演，其拉氏空间解对应的实空间井筒压力为：

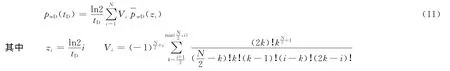
Buckley－Leverett油水两相渗流理论、多区复合油藏单相注入不稳定井底压力解和迭加原理就构成了注水井压力落差试井解释的基本理论。

2 实例计算

塔河油田碎屑岩油藏随着不断开采地层能量降低，将逐步转向注水开发以提高采收率。实例选自塔河油田的GK10注水井，井和油层的基本参数为：有效厚度4.5m，孔隙度24%，原油压缩系数6.14×10－4MPa－1，水的压缩系数4.42×10－4MPa－1，原油黏度4.998mPa·s，水的黏度0.6207mPa·s，关井测压前日注水量45m3，累积注水量3872m3，油层中深3704m。

通过非线性自动拟合法计算机自动拟合，拟合压力计算至与实测压力满意为止（图3），通过自动拟合可以计算出含水饱和度分布（图4）。非线性自动拟合法的结果分别是：表皮因数5.7，井筒储集系数2.9m3／MPa，水相渗透率15.7D，水驱前缘半径55.1m。统计了4井次碎屑岩注水压降，分别采用典型曲线分析法和非线性自动拟合法进行解释并对比，结果见表1。

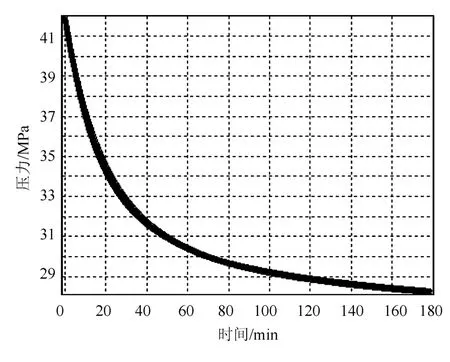
图3 实测与预测时间－压力曲线（几乎重合）

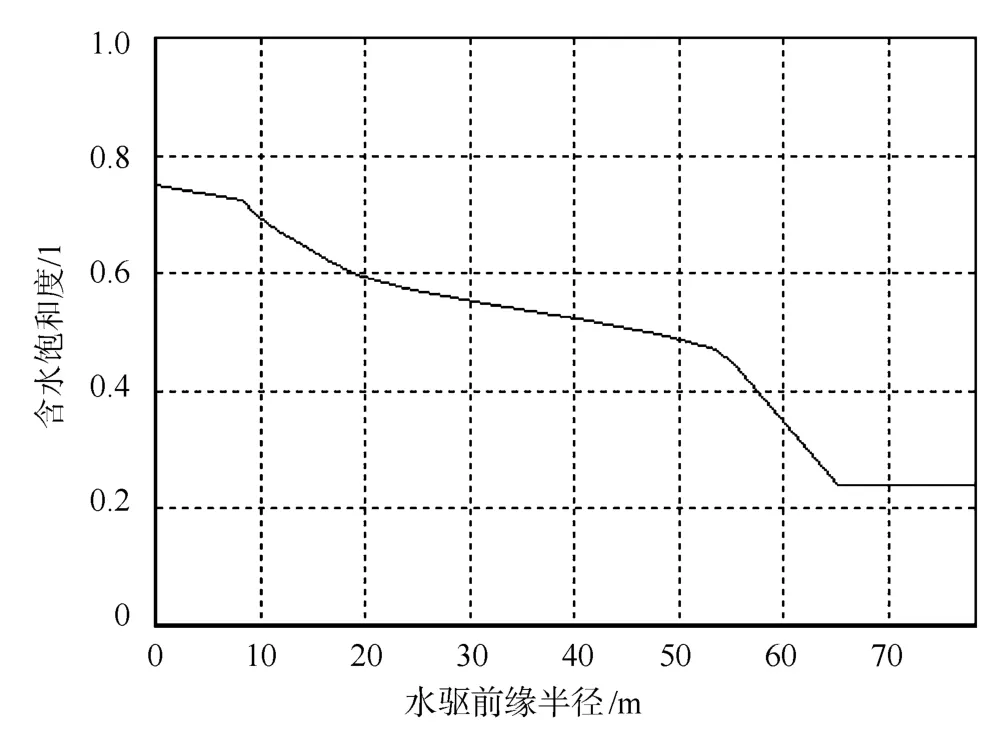
图4 含水饱和度分布

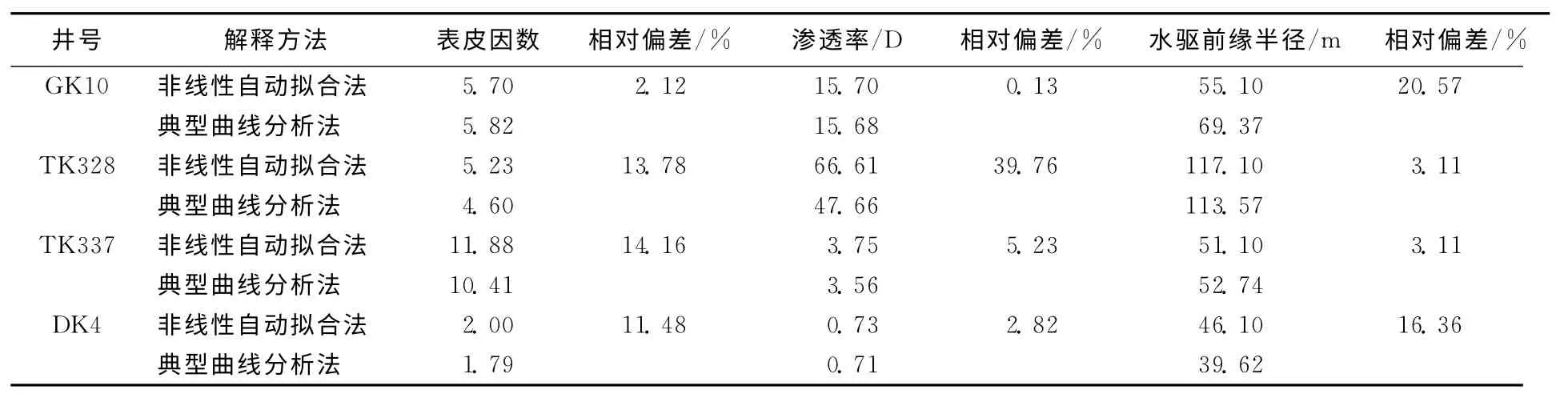
表1 非线性自动拟合法与典型曲线分析法解释参数对比表

通过表1可以看出，两种方法解释出的参数值相差较小，非线性自动拟合法解释出的参数值具有可信性。在油田实际解释中以典型曲线分析法计算出的参数值为非线性自动拟合法初始值，可以避免多解性且提高了准确性。

3 结论

1）利用多区复合油藏注水压降理论结合自动拟合解释方法，可以解释注水井井筒储集系数、表皮因数、渗透率和水驱前缘半径；结合油水相渗曲线，可以确定注水井周围含水饱和度分布。

2）通过典型曲线分析法和非线性自动拟合法结果的对比，其非线性自动拟合法结果真实可靠；采用常规试井方法作为本方法的初值，可提高解释参数准确性。

3）通过对砂岩油藏注水井单井试井资料的分析，解释水驱前缘推进状况，对表皮和水驱前缘有一个清晰的了解，可以完善油藏驱替动态监测资料解释，为油田注水开发提供依据。

［1］Nanba，Takao，Horne，etal.An improved regression algorithm for automated well－test analysis［J］.SPE18161，1992.

［2］Rosa A J，Horne R N，Stanford U.Automated well test analysis using Robust（LAV）nonlinear parameter estimation ［J］.SPE22679，1995.

［3］虞绍永.试井资料的计算机自动分析新方法 ［J］.石油钻采工艺，1991，11（6）：79～82.

［4］姚军，李春英，李爱芬.Gauss－Marquardt方法在试井解释中的应用 ［J］.油气井测试，1993，2（4）：72～78.

［5］尹洪军，翟云芳.基于自适应遗传算法的试井分析最优化方法 ［J］.石油学报，1999，20（2）：51～56.

［6］席少霖.非线性最优化方法 ［M］.北京：高等教育出版社，1992.

［7］Amina B.Injection／falloff testing of vertical and horizontal wells［J］.Dissertation Abstracts International，2007，68（1）：601～606.

［8］Chen S，Li G，Peres A M，etal.A well test for in－situ determination of relative permeability curves［J］.SPE96414，2008.