电磁波负性运动与媒质负电磁参数研究
黄志洵
(中国传媒大学信息工程学院,北京100024)
电磁波负性运动与媒质负电磁参数研究
黄志洵
(中国传媒大学信息工程学院,北京100024)
用经典力学分析有质有形物体的运动时,速度是矢量,负速度表示反向运动。但对无质无形的波的运动而言,速度可为标量,不能说负速度仅代表流向反了过来。该怎样理解这种现象的含意?对负波速(NWV)而言,例如当脉冲通过特定媒质时具有负群速(NGV),数值为c/ng(ng<0),它不仅比脉冲通过真空时的速度(光速c)快,而且快到进入媒质前就离开了媒质。由此本文提出了“电磁波负性运动”的概念,并将其与简单的“反向运动”相区别。我们必须接受D′Alembert方程的超前解,理解负速度概念。可以说,自然以她的真实和丰富给我们上了一课,今后她还将继续教导我们。
事物的二元性是世界的本质。在现代物理学中,电磁参数成为负值或电磁波作负性运动均常有发生。物理参数为正或为负的本身是自然界对称性机制之一,对其作研究是探索客观规律的一个新途径。
电磁波负性运动;超前波;负介电常数;负导磁率;左手材料
1 引言
人类最先认识的物质形式是那些有质有形的实物,小到一粒砂子,大到一颗行星。I.Newton[1]很好地解决了描述它们的方法,基本参数是质量(m)和动量(p=mv)。后者当中包含速度v,表明Newton对实物运动快慢的重视。波动是完全不同的另一种物质运动形式。电磁场和电磁波是无质无形的物态;虽然不能说对它们的认识与Newton力学完全无关(光压实验[2]表示光束落到一物体表面时后者将受力,证明光有动量),但其规律很不一样。那么什么是光?J.Maxwell说“光是电磁波的一种”;这是既正确又了不起的判断,但电磁波又是什么?1905年A.Einstein提出“光由大量光子组成”的假说[3],因此获得了1921年的Nobel物理奖;但他自己在晚年却说“虽经50年思考也不知光量子到底是什么”[4]。 1925年Einstein在巴西科学院演讲时未能回答听众提出的关于光的本质方面的问题[5],显示出这方面研究的艰难。1926~1927年诞生了量子力学(quantum mechanics,QM),可谓柳暗花明;但同时出现的“波粒二象性”难题至今仍困扰着科学家们[6]。
作为波科学研究的一部分,本文既关注负电磁参数研究的理论与实验,也讨论电磁波的负性运动。这些规律尚未被物理学界列入“对称性和守恒量”表格,只在“手征对称性”(chiral symmetry)的概念中稍有联系。我们认为,物理参数的为正或负,电磁波的正性运动或负性运动,都是自然界的对称性机制之一。笔者提出的“负性运动”一词有深刻的内涵,它与简单化的“改变方向”并不全同。本文印证了下述观点:一代又一代科学家确实越来越深入到了怪异的层次。
2 Wheeler-Feynman吸收者理论
1941年2月美国Princeton大学物理系举行了一场学术报告会。它由J.Wheeler组织,报告人是他的学生R.Feynman(23岁),内容是“电动力学中的吸收者理论”(theory of absorbers in electro-dynamics)。参加者中包含一些访问学者、杰出的物理学家,如E.Wigner,H.Russell,J.Neumann,W.Pauli,以及A.Einstein。这是Feynman第一次学术演讲,其观点有人反对也有人赞成。……后来似乎是太平洋战争的爆发影响了论文的发表,因为直到1945年Wheeler和Feynman[7]论文才出现在《Rev.Mod.Phys.》上面,题为“作为辐射机制的与吸收者相互作用”。“吸收者”一词对今天的读者是生疏的,其实它的意思是“接收者”(receiver),对电子学家来讲就是接收天线。它也可理解为“负载”(load),总之是可以吸收能量的东西。但Wheeler和Feynman是在粒子物理学层面思考的,与电子学家不同。
问题的提出是在1939年到1940年间,当时学者们正对电子理论存在的问题进行思考。Wheeler有句名言:“在任何领域找出最奇怪的事,然后进行探索”;他的研究生Feynman针对“电子自作用能无限大”的发散困难就这样做了。如电子是点粒子(半径r→0),电磁理论中的有关方程会导致无限大能量。关于这个问题,梁昌洪[8]有很好的推导阐述(见该书“札记一:静电场的自作用能”)。Feynman认为需要引入某种新的物理概念,他提出一个假定:电子不能对自己产生作用。他考虑了不同电荷间的相互作用,并构建出一种物理学、哲学理念,以解释那个最为普遍的现象——电磁辐射(光辐射)。Feynman后来说[8]:“太阳中的原子一振动,8分钟后我眼中的电子也因为一个直接的相互作用而开始振动”。他的早期想法则是在不出现电磁场的情况下(没有场作为媒介)发生电子间直接相互作用的可能性。
1940年秋Feynman向Wheeler指出,空间中一个单独电子不会有辐射,只有同时有源和接收者时才会有辐射。他分析了只有两个粒子的情况,向Wheeler提问说:“这种一个影响另一个,而又反作用回来的力,是否能解释辐射阻尼(radiation resistance)?”Wheeler则建议向这个双电子模型引入超前波(advanced waves)概念——过去这种Maxwell方程的解一直存在,只是不受重视。Feynman把这概念发展为电子与周围的多个“吸收者”之间的关系,即把辐射阻尼看作是由吸收者们的电荷以超前波形式对源的反作用。现在他们的理论有了对称性,但必须用向内移动、在时间上倒转的波。只是出现新的困扰——其在发射之前即回到了源头。但他们取人们习惯的迟滞波(retarded waves),以适当方式与超前波彼此抵消,从而避免了令人不快的矛盾。前提是所有辐射都保证在宇宙某处、在某时间会被吸收。这证明他们尚未敢于单独使用超前波。
Feynman注意到,在他之前早有人用“源和吸收者之间的作用”(an interaction between a source and an absorber)来解释电磁辐射。例如H.Tetrode(见:Zeit.f.Phys.,1922,Vol 10,317)认为,若空间中的太阳是孤独的而没有别的能吸收辐射的物体,它将不再辐射。对于辐射机制而言,吸收者的存在是必不可少的要素。…… Feynman的分析以下述假设为基础:①无电荷空间中一个被加速电荷不辐射能量;②对一个给定粒子的场作用仅由别的粒子造成;③这些场用半个推迟解与半个超前解之和来表示。他把所研究的课题称为“作用理论的超前效应”(advanced effects of the theory of action)。在论文的唯一图示中(图题是“一个不完全吸收体系的超前效应的例子”),总图被分成8个小图,配有以下说明:“①在源加速前的入射波;②这些入射波被吸收;③在加速时刻入射波会对源产生作用;④源受到作用是由于:碰撞粒子或其他的力或入射波;⑤源辐射出波;⑥一些辐射波被吸收;⑦持续向外的波永远离开;⑧向外的波除了符号的变化,看起来像是持续穿越空间的入射波”。……在这里,他所谓的入射波(incident waves)似乎不是外来的波,因为空间只有1个源;它像是返回到源的那个波,即产生反作用的波。
1965年Feynman曾谈到他对时间(过去和未来)的看法:“我们能记忆过去,但不能记忆未来;我们能做些什么以影响未来,但不能做点事情来影响过去。……世界的全部现象看来是朝一个方向演进。但在物理定律里,过去和未来没有任何区别。引力定律、电磁学定律的时间均可逆转。”J.Gleick[9]评论说,Wheeler和Feynman在1945年大胆提出一个“半是迟滞波、半是超前波的时间对称理论”,亦即在企图揭示粒子相互作用机制时,为了避免陷入过去、未来的矛盾,必须运用向内运动的波(时间上倒转运动的波),以使理论对称。迟滞波和超前波会抵销,前提是辐射最终会被吸收。(以上各处的着重号均为笔者所加)。
自1945年以后的几十年中,Feynman有众多科学贡献(量子电动力学、图解法、路径积分、超流动性、弱相互作用),但他没有回到“吸收者理论”上来,甚至很少提起。粒子物理学界和电磁理论专家们似乎亦未加重视。但在近年来,随着负波速研究的兴起和超材料(meta-materials)的发展,Wheeler和Feynman在上世纪40年代的工作重新引起关注。
Wheeler-Feynman的吸收者理论,与笔者曾详细论述的截止波导理论[10],似有相似之处。可以证明,两个交互作用的电抗性储存场可以产生一些有功功率,而单独一个场就不行。这种interaction表示大自然有某种奇妙的特性,正如单独一棵树木的存在,和把它放到有许多树的林中,情况是不同的!……虽然过去的研究并未发现在简单的互感耦合交流电路中[11]有波的负性运动(或说超前波)的存在,但在截止波导理论中笔者曾发现相位常数为负(β<0)的现象,这实际上是一种超前波。而且近期的研究表明[12],天线近区场有类消失态(evanescent-state like)的情况和由此导致的超光速群速甚至负群速(NGV),这就是本文论述的“负性运动”了!以上联想给人以一种“恍然醒悟”的感觉。不过,我们不认同“用迟滞波与超前波抵消”这一作法(这是几十年前的思路,现在用不着)。
3 电磁波负性运动的存在性
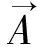

J.Maxwell于1856年给出
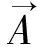
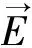
1865年Maxwell提出的20个标量电磁场方程经后人总结为4个矢量方程:
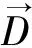
(1)
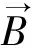
(2)

(3)
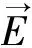
(4)
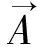
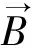
(5)
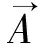

但对任意标量u,▽×▽u=0,故可假定一个标量Φ,满足
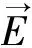
故有
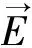
(6)
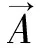
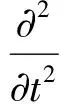
式中c是真空中光速;现在式(1)~式(4)可写作
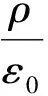
(1a)

(2a)

(3a)
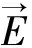
(4a)

(7)
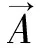
在满足Lorentz条件时可以证明:

(8)

(9)


(10)

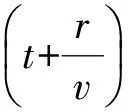
Maxwell-D′Alembert基础理论是严谨的,它告诉人们:自然规律并不像表面上看来那么简单。为了描写上述情况,笔者提出一个新词“电磁波负性运动”,英文可写作“negative characteristic motion of electromagnetic waves”。我们认为不能把它看作“反常”,而是一种自然所固有的正常物理现象。无论多么令人困惑,科学家都必须真实地反映客观世界的实情。更何况,近年来大量负波速实验已使超前波(advanced waves)理论得到了证实。
4 对“内向波”和“反向波”的讨论
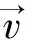
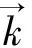
再次,不能只考虑等相位面的运动和相速矢量的方向。必须把群速放在重要的位置上来思考。虽然从1958年到2004年都有人简单地把“反向波”(backward waves)归结为“相速与群速的矢量方向相反”,但我们已指出把负速度一律当成“反方向的运动”并不恰当[16]。例如负群速(NGV)具有生动的物理表现,并非一个简单的“方向判断”所能描述。比方说,把向NGV媒质入射的脉冲与从NGV媒质出来的脉冲相比较,出射脉冲时间上可超前于入射脉冲(入射者尚未到达,出射者即现身)。这种“超前现象”(advanced phenomenon)导致了对因果性(causality)的新解释。刘辽[17]认为,causality的精髓在于“果不能影响因”,而非“因必在果之前”。如把输出脉冲当作“果”,输入脉冲到达当作“因”,实验证明可以发生“果先于因”。一定要懂得以“因先于果”为核心的causality只是一种经验和信念,而不是一个必须绝对遵守的定律。
可以证明,当定义相折射率n=c/vp,群折射率ng=c/vg,在引用Rayleigh公式时可证明有下述近似式成立[13]:
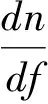
(11)
这里f是入射电磁波的频率;由此可知,由于LHM导致n<0,ng是否为负取决于dn/df的符号。若dn/df<0(反常色散),必有ng<0;如能在这种条件下经过电脑编程而演示,会更有意义。如媒质为正常色散(dn/df>0),ng为负的条件为
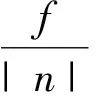
(12)
当然,即使不用LHM,即n>0,也可能获得ng<0——这条件就是反常色散(dn/df<0)。

v=λf
(13)
而波长λ和频率f都是标量。1972年由美国标准局(NBS)完成的对真空中光速c的最精确测量[18],就是以高度复杂的技术用激光进行光频测量和光波长测量(针对甲烷CH4),从而得出
c=λCH4fCH4=(299792456.2±1.1)m/s
(14)
经国际计量局修正后确定
c=299792458 m/s
(15)

5 物质的负电磁特性
V.G.Veselago是原苏联科学院Lebedev物理研究所的科学家,1964年他在俄文刊物《物理科学成果》上刊出论文(见Usp.Fiz.Nauk,vol 92,July 1964,517-526),译成英文的题目是“The electrodynamics of substances with simultaneously negative values ofεandμ”,在美国出版于1968年。Vesselago的科学思想是[15]:对于电磁波在物质中的传播而言,介电常数ε和导磁率μ是基本的特性参数;它们是物质色散方程中出现的表征物质电磁性能的仅有的两个量。对于各向同性媒质,色散方程具有简单形式:
(16)
式中n满足
n2=εrμr
(17)

假定用ε为横坐标、μ为纵坐标,构成一个坐标系。那么,可以对划分出来的4个象限,分析物质性态与电磁参数符号(正或负)的相互关系,见表1。表中的象限Ⅲ指明,ε<0、μ<0(ε、μ同时为负)属于“自然界不存在的情况”。那么是否有例外?比如说,2000年Wynne等[19]的实验,给出了圆截止波导的等效折射率(neff)为负的数据和曲线,是否“大自然也有负折射”的例子?我们认为不能这样看,因为金属壁波导本身也是一种人工制造的器件(或称媒质);故Vesselago的论断并未受到破坏。
现在从能量角度进行讨论,如所周知,凡静电场不为零的空间都储存着电能,它的推导是根据做功和守恒的原理,得出电场储能为
单位是J;积分域v是有电场的空间。场中任一点的电场能量密度用we表示,显然有
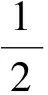
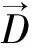
(18)
类似地,在恒流源产生磁场的理论中,凡磁场不为零的空间都储存着磁场能量:
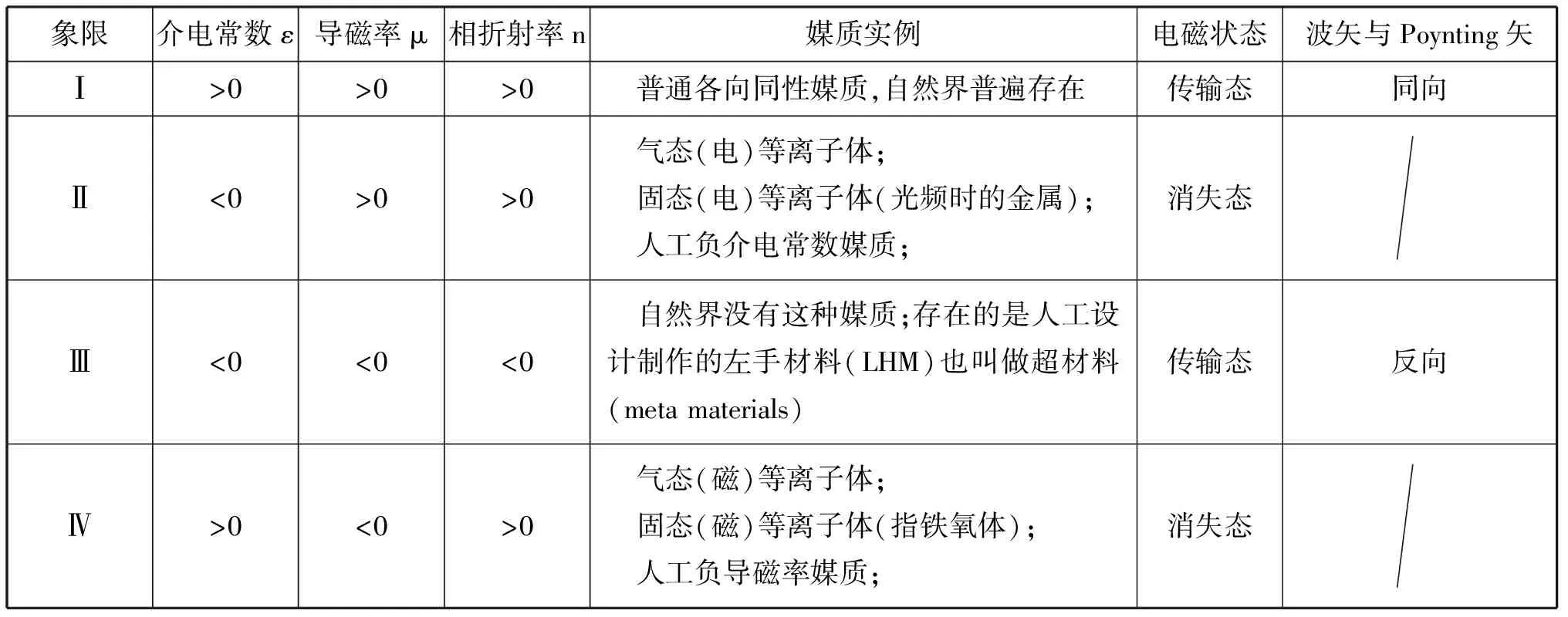
表1 媒质电磁特性的4种情形
场中任一点的磁场能量密度为
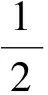
在各向同性媒质中为
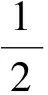
(19)
单位也是J/m3。
当我们考虑时变电磁场时,应把电场能、磁场能相加,可写出总能量密度:
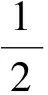
(20)
在Veselago理论中,ε<0和μ<0的同时实现要求存在频率色散(frequency dispersion,FD)。如没有FD,上式显示w<0,他认为不合理(不可能总能量密度为负)。在有FD时,应当用下式代替:
(21)
如果ε与ω无关、μ与ω无关(无色散),上式与(20)式相同。为保证w>0,要求
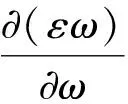
(22)
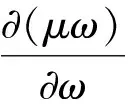
(23)
这两个不等式即使不满足,也不表示ε、μ不能同时为负。总之,ε、μ必与频率有关。因此Vesselago的观点可归纳为:负折射媒质并不意味着负能量。
由Maxwell电磁场理论可知,电场与磁场虽可共处于同一空间,却是各自独立的。但在另一方面,时变电磁场的规律是:变化的电场会激发磁场,变化的磁场会激发电场,二者相互依存又相互转化,形成不可分开的整体。因此,对于表Ⅰ中第Ⅱ、Ⅲ象限的情况(单独的ε<0或单独的μ<0),虽然由式(18)和式(19)可得负的电能或负的磁能,但总体情况却由(20)式决定;亦即得不出总能量为负的结论。
以上的Vesselago观点和我们的解释,对于说明“物质可以有ε为负、μ为负同时出现的状态”,是可以的。但存在一种对负能量(negative energy)作否定的意味,则是欠妥的。在量子力学Dirac波方程中,负能量和负能态概念的运用不仅成功,而且导致了正电子的发现,又引导出现了整个反物质物理学。亦即对负能量的排斥是经典物理所特有的,在量子物理中则不存在这种限制。后者把负能看作比量子起伏(量子涨落)能量还低的物理状态,具体例子如Casimir真空。笔者曾指出[20],当在空无一物的空间平行放置两块非常靠近的金属板,改变了真空的结构——造成了两种真空,即板外的常态真空和板间的负能真空(vacuum of negative energy)。这时负能量表示空间区域的真空程度比空无一物还要空,从而单位体积的能量(能量密度)小于零。负能量概念是可以有的!
因此,作为经典物理学成果之一的Vesselago理论,虽然近年来取得了很大的成功;但它仍然有待提高到量子物理学的层次。这将是未来的有兴味的研究工作。
6 怎样获得负介电常数
我们先看表1中第Ⅱ象限的情况,即ε<0、μ>0的媒质。论述的次序是:气态(电)等离子体→固态(电)等离子体→获得负介电常数的人工方法(Pendry法);其中所谓固态(电)等离子体实际上是金属。1999年出版的笔者所著书《超光速研究——相对论、量子力学、电子学与信息理论的交汇点》[21],其中有一篇论文“波在电离气体中的截止现象和消失场特性”。该文很好地分析论述了电磁波通过等离子体时的截止现象和呈现出来的消失场特性,实际上是根据截止波导理论[10],结合气体等离子体的特点而进行研究。但该文忽略了分析和计算相对介电常数,并未对其“可能为负”提出证明。
所谓气态等离子体(gas plasma)是指这样的物质形态——一种不定形、可流动和扩散、密度较小的体系,包含中性粒子、正离子及大量电子,总体上呈现电中性。这是一种带电粒子均匀分布的电离气体,但其内部的极化作用和Coulomb力作用都表明它是与其他介质不同的媒质,是一种新的物质形态(第4态)。由于电子浓度(体密度)很大,在入射电磁波频率较低时(例如f<50MHz)可视为导体。但正如笔者的论文[19]所指出的,在较高频域存在着电磁波不能通过的截止区(例如f=50 MHz-500 GHz),而在更高的频域(例如f>500 GHz)呈现电介质特性。因此,说“等离子体象导体”,只在一定条件下正确。以上的频率分界数据是氢等离子体的情况,只是举例而已。
从表面上看,金属这种有固定形状的坚硬物质,与气态等离子体毫无共同之处。但金属的组成是晶格和自由电子气,而后者名称的由来可由下述事实看出:金属的电子浓度(ne)比气态等离子体高出很多,甚至可达8个数量级。实际上,两者对某些物理参数[例如等离子振荡频率(ωp=2πfp)]有相同的定义方式;两者都用复数介电常数(以及折射率)进行描述;如此等等。在许多科技领域中,对二者的理论都要借鉴参考。
在一定条件下,气态等离子体的相对介电常数(εr)可能为负。这里主要讨论εr的实部,可以写出:
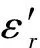
(24)

(25)
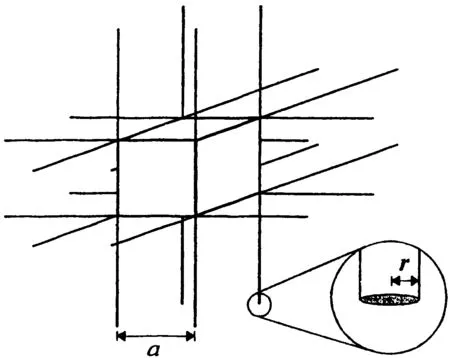
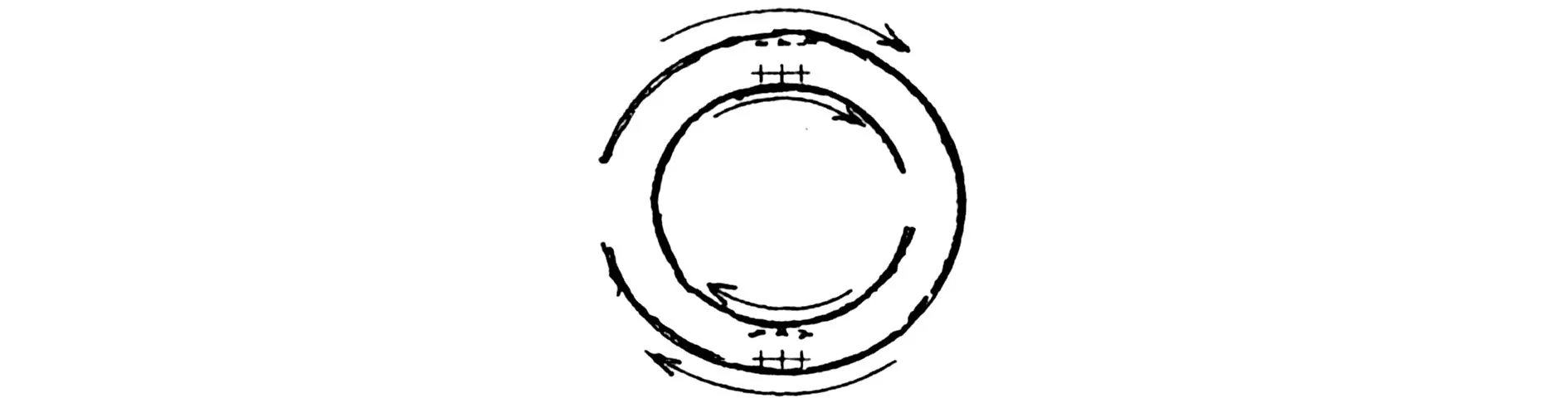
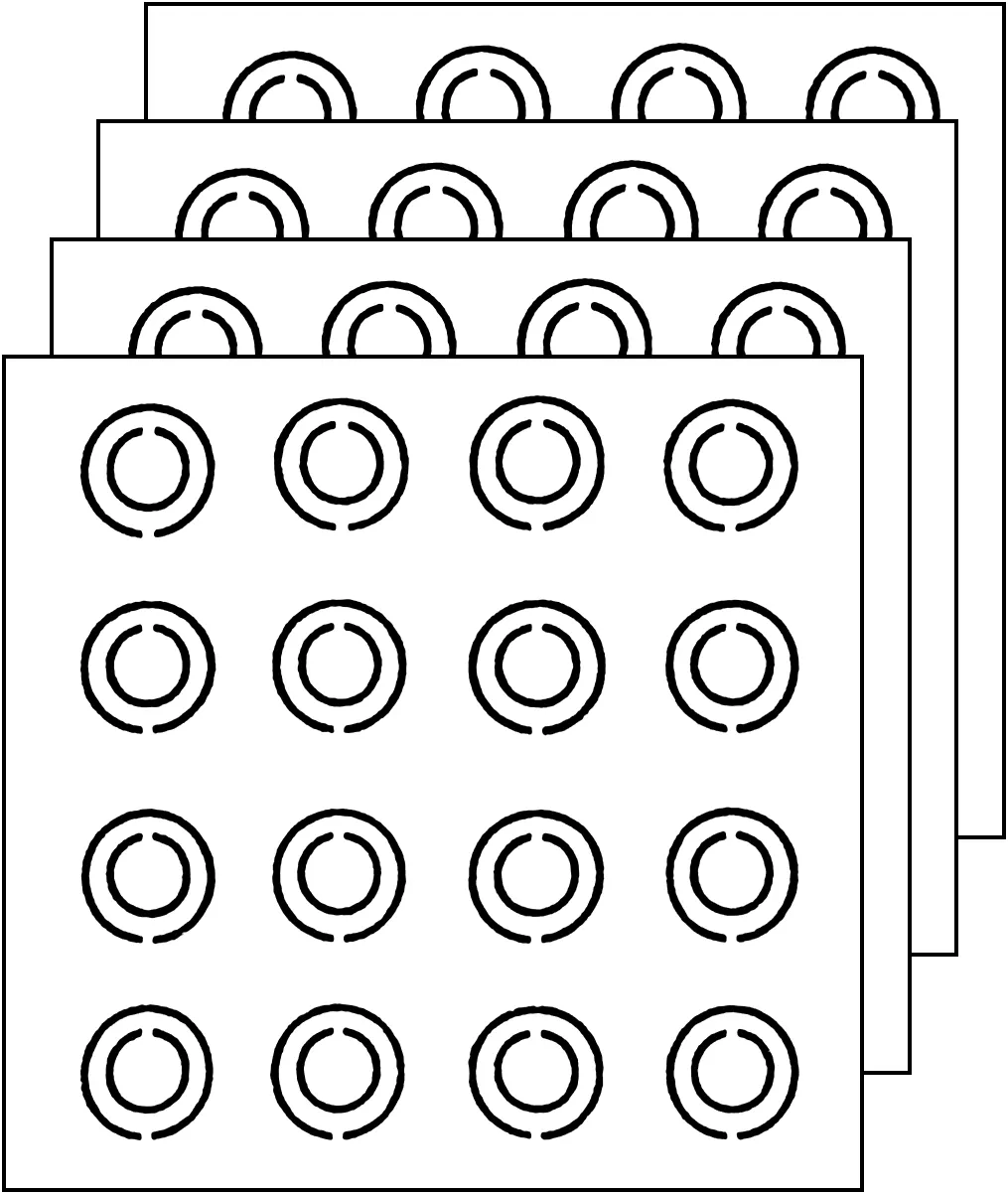
f (26) 但我们的注意力主要放在所谓“固态等离子体”(金属)方面。金属介电常数是一个经典物理学可以处理的宏观电磁问题。尽管如此,还是应当区分以下两种不同情况——大块金属与极薄(例如纳米级)金属膜。它们的ε值是否有差别,以及差别的大小,是应当加以考虑的。一般的理论分析均指前者;金属相对介电常数算式为[22] (27) 式中ωp是等离子振荡频率: (28) (29) (30) 我们曾指出[22],铝的Fc=1.94×1013Hz,fp=5.7×1014Hz,前者在远红外区,后者在红外与可见光交界处。对于大块金属情况,在微波由于ω相对较低,就有f=0 ~Fc区域的算式: (31) 因而“介电常数为负值”是能做到的;然而在ω≪Fc时(微波即此)有 (32) 当f>Fc,金属相对介电常数实部为: (33) 表2 金属的负介电常数 对金属薄膜介电常数的测量需作些解释。在f 图1 金属线阵 (28a) 式中n和m的下标eff表示“有效值”;对铝而言ωp=15ev,另一参数=0.1ev(对应本文的Fc)。用细导线阵组成的新媒质可使ωp降低6个数量级,而线阵是周期性结构,它可看作图1中所绘的立方体点阵组成的。这一结构产生两方面的效果,首先是有效电子密度的下降是由于金属体积减小,由a2L变成πr2L(L为金属纵向尺寸),因而有 (34) 显然可得neff≪ne。 另一方面,电子有效质量的加大是由于入射波电场方向与金属丝方向相同时后者的电感作用使电子运动减慢。经推导得到 (35) 对于铝线阵,取r=10-6m,a=5×10-3m,ne=5.68×1017m-3;可算出 meff=2.48×10-26kg=2.72×104me 最终得到ωp=8.2 GHz,进入微波范围。这样一来,本来处在光频区的fp可降到微波频段。现在可用下式计算Fc: (36) 式中σ是金属的有限导电率;然后,可由前述公式获得线阵的介电常数,并获得εr<0。 虽然Pendry论文没有给出系统的计算数据,更未做实验,但后人对其思想作验证发展的论文很多。例如2004年的Panoiu[30]计算不仅是为了观察负参数(-ε、-μ、-n)的数值规律,更是为了探索已有方法用到光频的可能性。他用传输矩阵法(transfer matrix method,TMM)计算了直导线阵和SRR组合系统的有效介电常数(εr)和有效导磁率(μr),掌握了这些参数与频率的关系,他称为频率色散(frequency dispersion)。为了探索这种构建超材料的方法上限,他采用的是微米级的结构,对直导线阵而言取ωp=7.5×1015Hz,Fc=(1-4)×1013Hz。图2显示εr的实部为负数,虚部为正数(但不大)。 图2 金属线阵在红外区的相对介电常数 (a) (b) 表1中第Ⅲ象限的情况是ε>0、μ<0;在这里我们略去自然界是否存在这种媒质的讨论,而直接关注人工设计和制作的负导磁率媒质。1999年J.Pendry[31]就可产生负导磁率的人工系统提出了A、B、C共3个方案,其中B称为split ring cylinders array(开口环圆柱阵列),更确切的称呼是金属的开口环谐振腔(split ring resonator,SRR),形状见图3(a);后来由于广泛采用印制电路板技术和真空镀膜技术,流传下来的方法是平面化的结构,见图3(b)。作为基本单元的SRR,由内环(inner core)和外环(outer ring)组成,而这两者都有缺口。两个金属平面环之间的间隔为g,裂口宽度为s,内芯直径为2r,两个金属条的宽度均为t。当入射波磁场方向与环的轴向具有相同方向,内外环间的电容及两环的自感构成谐振器,其电流将产生一个附加的感应磁场。……虽然不是一个SRR单元就能提供负导磁率,但Pendry的推导计算却是以单个unit为基础的。当有磁场与图3(a)的圆柱平行,在开口环上感应的电流见图4,而两环间有电容是重要的。细致的推导得到 图4 两环上感应的电流示意 (37) 式中F=πr2/a2是填充系数,Г、ω0分别为谐振宽度和谐振频率: (38) (39) 式中l是板的间距,ρ是电阻率,c是光速;对于良导体(例如铜、银),可取ρ≅0,故有 (40) 由上式可以证明,当 (41) 将有μeff<0;令“磁等离子频率”(magnetic plasma frequency)为 (42) 故获得负导磁率条件为 ω0<ω<ωmp (41a) 这种情况见图5;故可知,新结构只是在导磁率色散特性(μeff~ω关系)中有一个负值的“窗口”。 图5 SRR有效导磁率与频率的关系 图6 SRR在红外区的相对导磁率 图7 多层SRR阵列 必须注意Pendry计算(图5)与Panoiu计算(图6)的区别;Pendry取r=2×10-3m=2mm,α=5×10-3m=5mm,d=1×10-4m=0.1mm(注:他的d即图3(b)中的g);亦即在毫米级尺寸下计算,结果呈现在微波(f0=2.94GHz,fmp=4.17GHz)。Paniu是在微米级尺寸下计算,结果呈现在光频。但两者在原理上并无不同。……可贵的是,1999年Pendry还提出了具有3D对称性的SRR单元的设计思想,见图8;这对尔后的发展是有重要意义的。 图8 SRR的3D对称性设计 有趣的是,有研究者发现SRR除了在某个频段呈现负导磁率特性,在更高频域可能出现负介电常数特性;而两者难以在同一波段共生,因而不满足获得负折射率的要求。为此改SRR为S型结构[33],实现了两种现象在同一频域并存。这时金属线阵可以不要!由此可知,SRR阵列经改进后就成为一种新型的人工超材料。 在粒子物理学中,自旋为1/2的粒子有两种独立的自旋状态,一种区分法称为手征(chiral),两种状态即左旋和右旋。1992年M.Saadoun[34]讨论了电磁手征性(electromagnetic chirality)和手征媒质(chiral media),建议了一种Ω形微结构(Ω-shaped microstructure),如图9(a),它是由单匝螺旋变形而得。多个单元可形成阵列。见图9(b),它可称为Ω媒质(Ω medium),我们称为Ω环结构或Ω环阵列。一旦把它看成为一种物质或材料,就产生如何应用的讨论,例如在矩形波导中沿z向作部分填充。 (a) (b) 在基础的电工学中不乏手性规则,由于导线切割磁力线就会产生电动势,有所谓“发电机右手定则”(大拇指指示导线运动方向时,4指方向是电动势方向)。又如在自感线圈中,如4指为线圈中电流方向,大拇指为磁场方向(N极)。……因此,图9(a)的结构和图9(b)的阵列,自有其手征效应。而利用两个Ω型结构相对放置,可以去除其手征效应。 新材料设计都追求各向同性(isotropic);它表示电磁波无论从何方向入射,其性质都相同。Pendry的两个方法(负ε和负μ)显然不满足这一要求,因它们只有在传播方向与导线轴向或SRR轴向正交时才能得到(-ε)和(-μ)。……如采用Ω形结构进行设计,暂不要求各向同性,可取图10,此为单面的形状。另一面的形状相同但位置相反,图中未画出。2004年Huangfu等[35]的设计即以此为基础,用双面的3个互相连接的Ω环。用FR4基板,它高10mm,厚0.4mm,ε=4.4(当f=10GHz);类Ω结构印刷在基板两面,按相反方向。环半径为1.4 mm,其他尺寸为:a=0.4mm,b=1.5mm,c=2.9mm,L=4mm。作为阵列,x方向共10个单元,y方向共80个板。估计总尺寸为4×4×4cm3,这比几年前某些文献制备的超材料小多了。另一个例子是,2010年夏颂[36]用这种典型的Ω形LHM进行了研究,其环半径为1.5mm及1.9mm,其他尺寸为:a=0.4mm,b=2.8mm,c=4.6mm,L=5mm;基板刻有Ω环的PC板厚1mm,未刻的厚2mm;基板材料为FR24。每片有10个基本单元(每单元只有2个Ω环),共8片。整个LHM呈长方形,最大尺寸估计约为6cm,但较窄小(宽度约1.2cm)。 图10 双面3环Ω形结构的正面 图11是Ω形结构的有效导磁率曲线示例(引自L.Ran[37]),几何参数为:L=0.5mm,h=0.5mm,r=1.5mm,d=0.1mm。可以看出,只有在频率高于一定值时才得到负导磁率;Reμ的变化规律与图6相似。 图11 Ω形结构有效导磁率示意 如果要求各向同性,则可参照2003年C.Simovski[38]的方法。图12(a)是Ω粒子立方晶胞的几何结构。为了图形的清晰,只有一对Ω形理想导体粒子被展示在立方晶胞相对的2面。图12(b)是多个立方晶胞(每面都有6个Ω环)形成的阵列。但该论文主要是理论分析,缺乏实验。实际的技术,比用多层结构困难得多。 (a) (b) 本文的一个重点是提出和研究波的负性运动。在Newton力学所处理的有形有质之物的运动中,速度是矢量,这时只有正向运动和负向运动(负速度即代表反向)。但对于无形无质的波,速度可以是标量,负速度不一定代表反向运动,而是另有含意,例如表达一种看来奇特的情况——“输出波形出现在输入波形到达之前”,“发射出来之前即已接收”,“波向源处集中”;等等。正如说“一位叫Birght的姑娘今天离家出走,在昨天傍晚她到达了目的地”;这种表面看来荒谬的事在波科学中却存在!为了理解它,必须认识到这只在“速度是标量而又为负值”的情况下才会发生,其次应当对Causality有更高明的认知。这些就是本文提出“电磁波的负性运动”概念的基础,显然它与波的“负向运动”不是一回事。 对电磁波负性运动概念,要承认其存在的合理性和在科学研究中的意义。关键在于正确认识Maxwell-D′Alembert方程的超前解,将其放在应有的合理位置上。与此相联系的是要理解和接受负速度。这时人们对自然界的认识将提高到一个新的层次。 对负电磁参数的讨论是本文的另一重点。必须指出,J.Pendry的设计思想(1996年、1999年论文)功不可没,正是靠它们做出了最早的LHM。然而近年来对Pendry方法(把两个功能系统组合在一起以获得LHM)已逐渐放弃,改为设法在单一结构中同时产生(-ε)和(-μ),并造成一个左手频带(Left-handed band)。在这种努力中,从造成负导磁率系统中发现产生负介电常数的可能性,成为一些科学家乐于从事的工作,由此又不断衍生出新的设计。这种趋势是令人感兴趣的! [1]Newton I.Philosophiae naturalis principia mathematica[M].London:Roy Soc,1687.中译:牛顿.自然哲学之数学原理.王克迪译.西安:陕西人民出版社,2001. [2]郑华炽.Lebedev的光压实验[J].物理通报,1956,(3):148-151. [3]黄志洵.论单光子研究[J].中国传媒大学学报(自然科学版),2009,16(2):1-11. [4]Einstein A.50年思考还不能回答光量子是什么[A].范岱年,赵中立,许良英编译.爱因斯坦文集(第2卷) [M].北京:商务印书馆,1977. [5]黄志洵.超光速研究的理论与实验[M].北京:科学出版社,2005. [6]黄志洵.光是什么[J].中国传媒大学学报(自然科学版),2007,14(4):1-9. [7]Wheeler J A,Feynman R P.Interaction with the absorber as the mechanism of radiation[J].Rev Mod Phys,1985,17(2、3):157-181. [8]梁昌洪.电磁理论前沿探索札记[M].北京:电子工业出版社,2012. [9]Gleick J.Gennius:the life and science of Richard Feynman[M].London:Newton Publ Co Ltd,1992. [10]黄志洵.截止波导理论导论[M].北京:中国计量出版社,1991. [11]黄志洵.消失场能量关系及WKBJ分析法[J].中国传媒大学学报(自然科学版),2011,18(3):1-17. [12]黄志洵.自由空间中近区场的类消失态超光速现象[J].中国传媒大学学报(自然科学版),2013,20(2):40-51. [13]刘慈香等.异向介质中的内向波[J].中国科学院研究生院学报,2006,23(6):815-820. [14]Budko N V.Observation of locally negative velocity of the electromagnetic field in free space[J].Phys Rev Lett,2009,102:020401 1-4. [15]Veselago V G.The electrodynamics of substances with simultaneously negative values of permittivity and permeability[J].Sov Phys Usp,1968,10(4):509-514. [16]黄志洵.负波速研究进展[J].前沿科学,2012,6(4):46-66. [17]刘辽.试论王力军实验的意义[J].现代物理知识,2002,14(1):27-29. [18]Evenson K M,et al.Accurate frequency of molecular transitions used in laser stabilization:the 3.39μm transition in CH4and the 9.33 and 10.18μm transition in CO2[J].Appl Phys Lett,1973,22:192-198. [19]Wynne K,et al.Tunneling of single cycle terahertz pulses through waveguides[J].Opt Comm,2000,176:429-435. [20]黄志洵.论Casimir效应中的超光速现象[J].中国传媒大学学报(自然科学版),2012,19(2):1-8. [21]黄志洵.超光速研究——相对论、量子力学、电子学与信息理论的交汇点[M].北京:科学出版社,1999. [22]黄志洵.金属电磁学理论的若干问题[J].中国传媒大学学报(自然科学版),2011,18(4):1-12. [23]Schulz L G.The optical constants of silver,gold,copper and aluminm[J].J Opt Soc Am,1954,44:357-362. [24]Chen W P,Chen J M.Use of surface plasma waves for determination of the thickness and optical constants of thin metallic films[J].J Opt Soc Am,1981,71(2):189-191. [25]Weaver J H,Frederikse H P.Handbook of chemistry and physics[M].New York:CRC Press,2004. [26]Jiang R,Huang Z X,et al.Used surface plasma wave measure the thickness and the negative permittivity of nano-metal film[J].2013 Intern Conf on Energy Res and Power Eng,Zhengzhou China,May 24-25,2013. [27]Went H E,Sambles J R.Resonantly coupled surface plasmon polaritons in the grooves of very deep highly blazed zeroorder metallic gratings at microwave frequencies[J].App Phys Lett,2001,79(5):575-577. [28]Kretschmann E.The determination of the optical constants of metals by excitation of surface plasmons[J].Z Phys,1971,241:313-324. [29]Pendry J B.Holden A J,et al.Extremely low frequency plasmons in metallic mesostructures[J].Phys Rev Lett,1996,76(25):4773-4776. [30]Panoiu N C,Osgood R M.Numerical investigation of negative refractive index metamaterial at infrared and optical frequencies[J].Opt Comm,2003,223:331-337. [31]Pendry J B.Holden A J,et al.Magnetism from conductors and enhanced nonlinear phenomena[J].IEEE Transactions on Microwave Theory and Techniques,1999,47(11):2075. [32]Smith D R,Padilla W J,et al.Composite medium with simultaneously negative permeability and permittivity[J].Phys Rev Lett,2000,84 (18):4184-4187. [33]Chen H,Ran L,et al.Left-handed material only composed of S-shaped resonator[J].Phys Rev E,2004,70:057605. [34]Saadoum M,Engheta N.A reciprocal phase shifter using novel pseudochiral or Ω medium[J].Microwave Opt Tech Lett,1992,5:184;又见:Simovski C,He S.Frequecy range and explicit expressions for negative permittivity and permeability for an isotropic medium formed by a lattice of perfectly conducting Ω particles[J].Phys Lett,2003,A311:254. [35]Huangfu J,et al.Experimental confirmation of negative refractive index of a metamaterial composed of Ω-like metallic patterns[J].Appl Phys Lett,2004,84 (9):1537-1539. [36]夏颂.左手材料微波电磁特性测试技术研究[D].西安:西安交通大学博士学位论文.2010. [37]Ran L,Huangfu H,et al.Experimental study on several left-handed metamaterials[J].Prog Electro Res,2005,51:249-279. [38]Simovski C R,He S.Frequency range and explicit expressions for negative permittivity and permeability for an isotropic medium formed by a lattice of perfectly conducting Ω particles[J].Phys Lett A,2003,311:254-263. StudyontheTheoryofNegativeCharacteristicElectromagneticWaveMotionandtheNegativeElectromagneticParameters HUANG Zhi-xun (Communication University of China,Beijing 100024,China) When we use the classical-mechanics analyze the motion of substance,who has inherent mass and shape,the velocity is vector,then the negative velocity express backward direction.But when we discuss the motion of waves,who has not inherent mass and shape,the velocity is scalar,the negative velocity does not obey that rule,i.e.does not indicate only the direction of movement is flow backward.But what does that phenomenon mean? The negative wave velocity(NWV)means that,for example,a pulse propagates in special medium with a negative group velocity(NGV) ofc/ng(ng<0),then it is not only faster than a pulse travelling in vacuum,but so quickly that if left the medium before it had even finished entering.In this paper,we establish the concept of “negative characteristic motion of electromagnetic waves”,and we differentiate it from the meaning of “movement in backward direction”.We must receive the advanced solution of D′Alembert equation,and understand the concept of negative wave velocity.The truthful and rich of Nature give a lesson for us,and she will still instruct us continually in the future. The dualistic nature of matter is basic feature of the world;and the possibility of electromagnetic parameters in modern physics become negative value or negative characteristic motion of electromagnetic waves can exist everywhere.The positiveness and negativeness of physical parameters are one of symmetry in nature.Then,the study on this investigation area is the new way for research of objective laws. electromagnetic wave negative characteristic motion;advanced waves;negative permittivity;negative permeativity;left-handed medium 2013-05-13 黄志洵(1936-),男(汉族),北京市人,中国传媒大学教授、博士生导师,中国科学院电子学研究所客座研究员。 O415 A 1673-4793(2013)04-0001-15 (责任编辑:王谦)
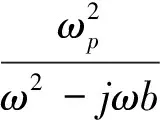
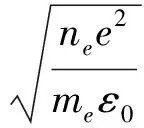
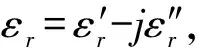
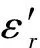
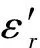
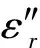
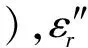
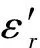

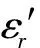

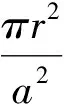
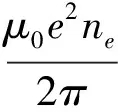
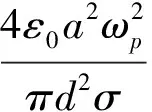

7 怎样获得负导磁率

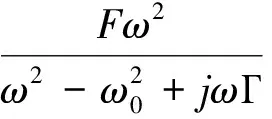
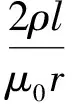

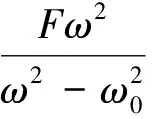
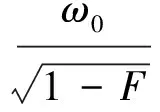
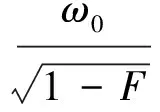
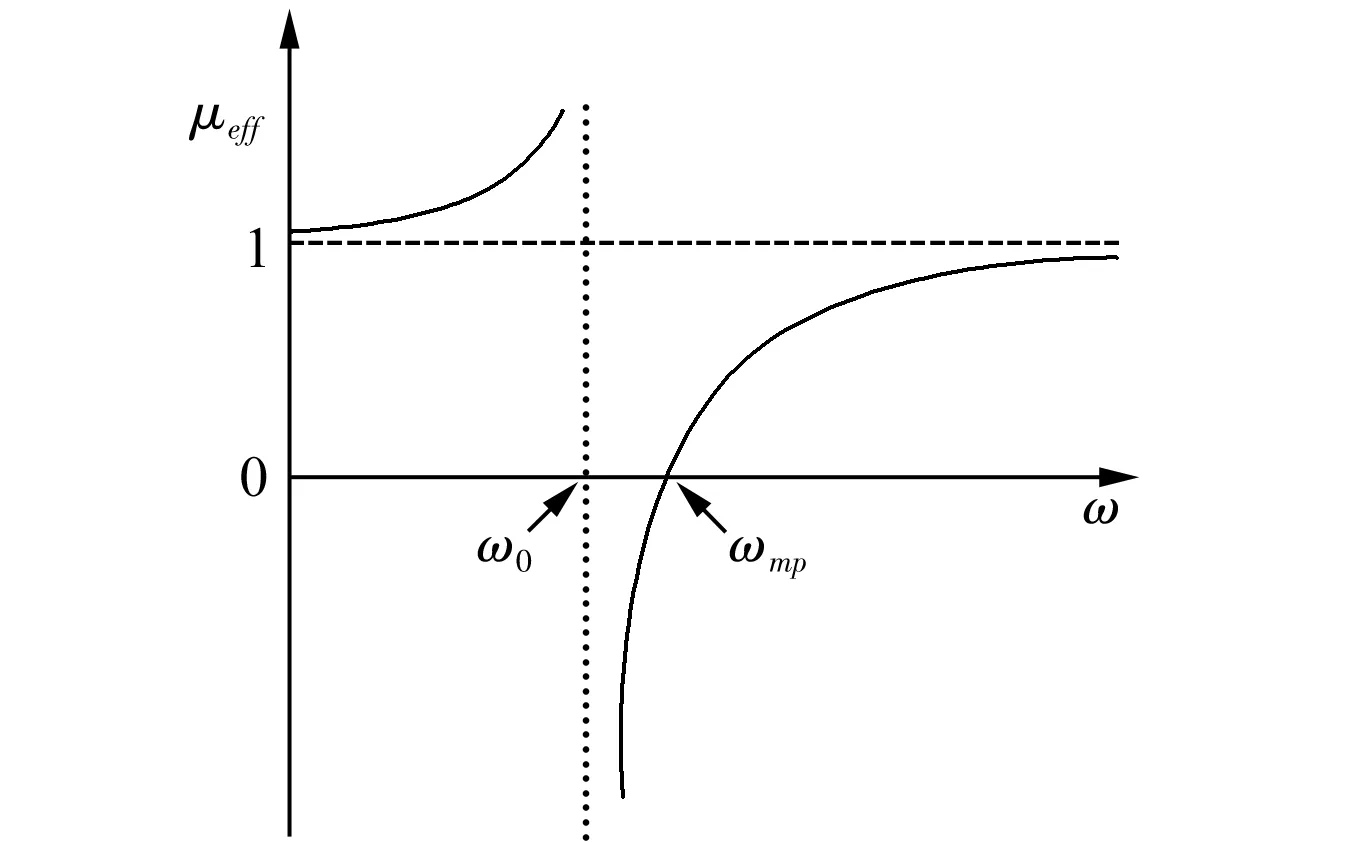
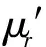

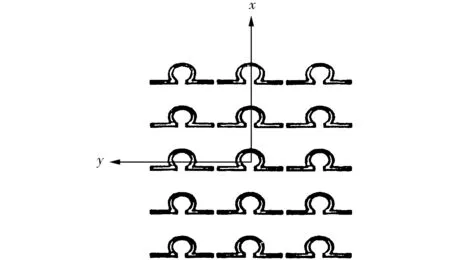
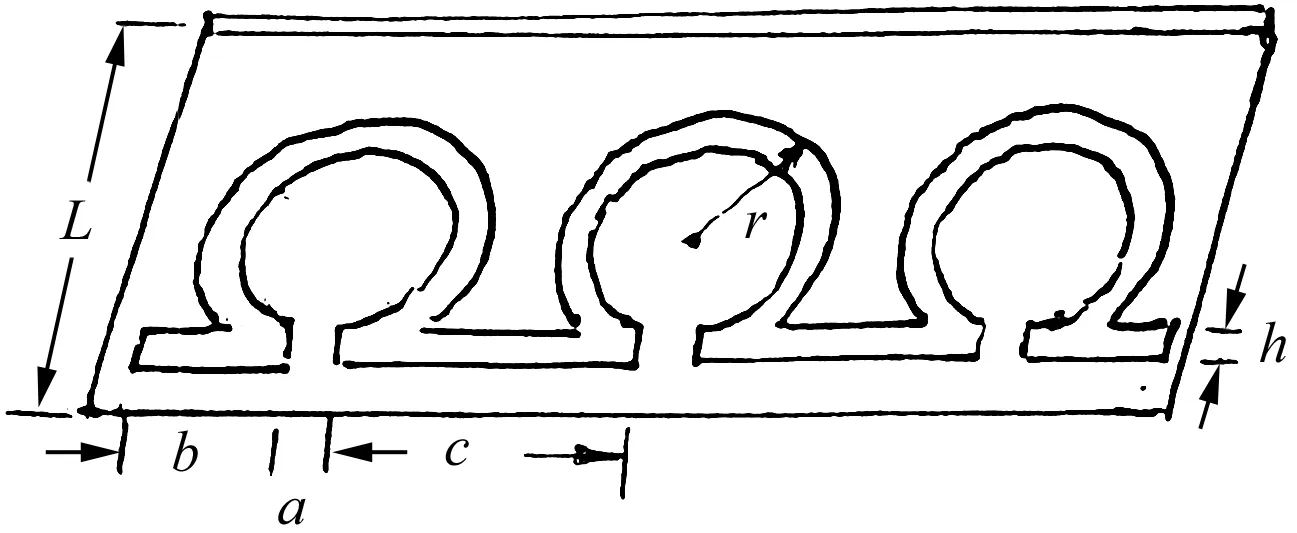
8 Ω环结构



9 结束语


