基于多点地质统计算法的多重网格研究

王家华 (西安石油大学计算机学院，陕西 西安 710065)

王孝超 (西安石油大学石油工程学院，陕西 西安 710065)

李石权 (中石化中原油田分公司采油一厂地质所，河南 郑州 457001)

李占岭 (西安石油大学石油工程学院，陕西 西安 710065)

基于多点地质统计算法的多重网格研究

王家华 (西安石油大学计算机学院，陕西 西安 710065)

王孝超 (西安石油大学石油工程学院，陕西 西安 710065)

李石权 (中石化中原油田分公司采油一厂地质所，河南 郑州 457001)

李占岭 (西安石油大学石油工程学院，陕西 西安 710065)

多点地质统计学相比于传统的地质统计学具有明显的优势，能够描述几何形状较复杂的河道砂体等的连续性和变异性。介绍了多点统计算法的基本原理及具体执行步骤，阐述了多重网格思想，并对多重网格数及其对模拟结果的影响进行了研究。

多点地质统计学；储层建模；多重网格

传统地质统计学利用变差函数来描述地质变量的变异性和相关性。变差函数建立在两点统计关系之上，仅仅反映空间上两点之间的相关性，其很难描述几何形状比较复杂的河道砂体等的连续性和变异性。多点地质统计学建立在多个点的相关关系上，其利用训练图像代替变差函数来描述地质变量的连续性和变异性。因此，在实际应用中，多点地质统计学表现出很大优越性。下面，笔者基于多点地质统计学对多重网格进行了研究。

1 多点统计算法

多点统计建模方法包括迭代类算法和非迭代类算法[1-2]。由于迭代类算法存在迭代收敛的局限，其应用受到极大限制。非迭代类算法从训练图像中直接提取局部条件概率,并应用序贯指示模拟方法进行模拟实现[3]，该算法不存在迭代收敛的问题,因而算法简单。但由于在每模拟一个网格节点时均需重新扫描训练图像以获取特定网格的局部条件概率，因此严重影响计算速度[2]。2001年Strebelle等[4]基于多点地质统计学原理对非迭代类算法加以改进后提出多点统计算法,应用一种动态数据结构(即“搜索树”)一次性存储训练图像的条件概率分布并保证在模拟过程中快速提取,从而大大提高了计算速度。

图1 数据模板、训练图像和数据事件

1.1多点统计信息的获取

多点统计算法通过数据模板扫描训练图像获得多点统计信息。由n个向量{ha；a=1，2，…，n}构成的几何形态定义为数据模板。令u为模板中心点，其他位置为ua=u+ha。假设一种属性s可取m个状态，由数据模板中的n个向量ua以及其各位置的n个属性值组成了“数据事件”(见图1)。

1.2算法执行步骤

多点统计算法的具体执行步骤如下[5-6]：①根据前人的研究成果，做出符合地质实际的训练图像。②由用户自己定义与数据搜索临域有关的搜索模板来扫描训练图像并建立搜索树。③将测井数据瞄定在最近的网格节点上，并定义一条对取样节点进行访问一次的随机路径。④确定未取样点条件概率。⑤序贯模拟。重复④、⑤步骤，直到所有节点都被模拟，从而产生一个随机模拟实现。

2 多重网格

2.1多重网格思想

图2 多重网格图

要使训练图像包含所有可能的数据事件是不可能的，加之受计算机CPU的限制，因而只能选取合适大小的数据模板[7-8]。基于此，Tran[9]提出了多重网格的思想，其主要目的是描述小规模结构和大规模结构，具体执行方法如下。最粗(低精度)网格首先被填入，最细网格最后被填入。在最粗网格中，每个2(m-1)个(m为多重网格的数量)单元格就有1个被处理(如图2(a)的黑色单元格)。在次粗网格中，这些单元格作为已定义节点来使用(如图2(b)的黑色单元格)。使用次网格是指那些正好处于已定义单元格中心的次一级单元格,其将被首先填入黑色，其他的次一级单元格之后填入白色。如此运行直至所有单元格都被处理完为止(见图2(c))。

根据以上论述，可看出对应第g重网格的第g重数据模板为:

图3 数据模板

注：图中黑色表示泥岩，白色表示河道。

2.2多重网格的选择

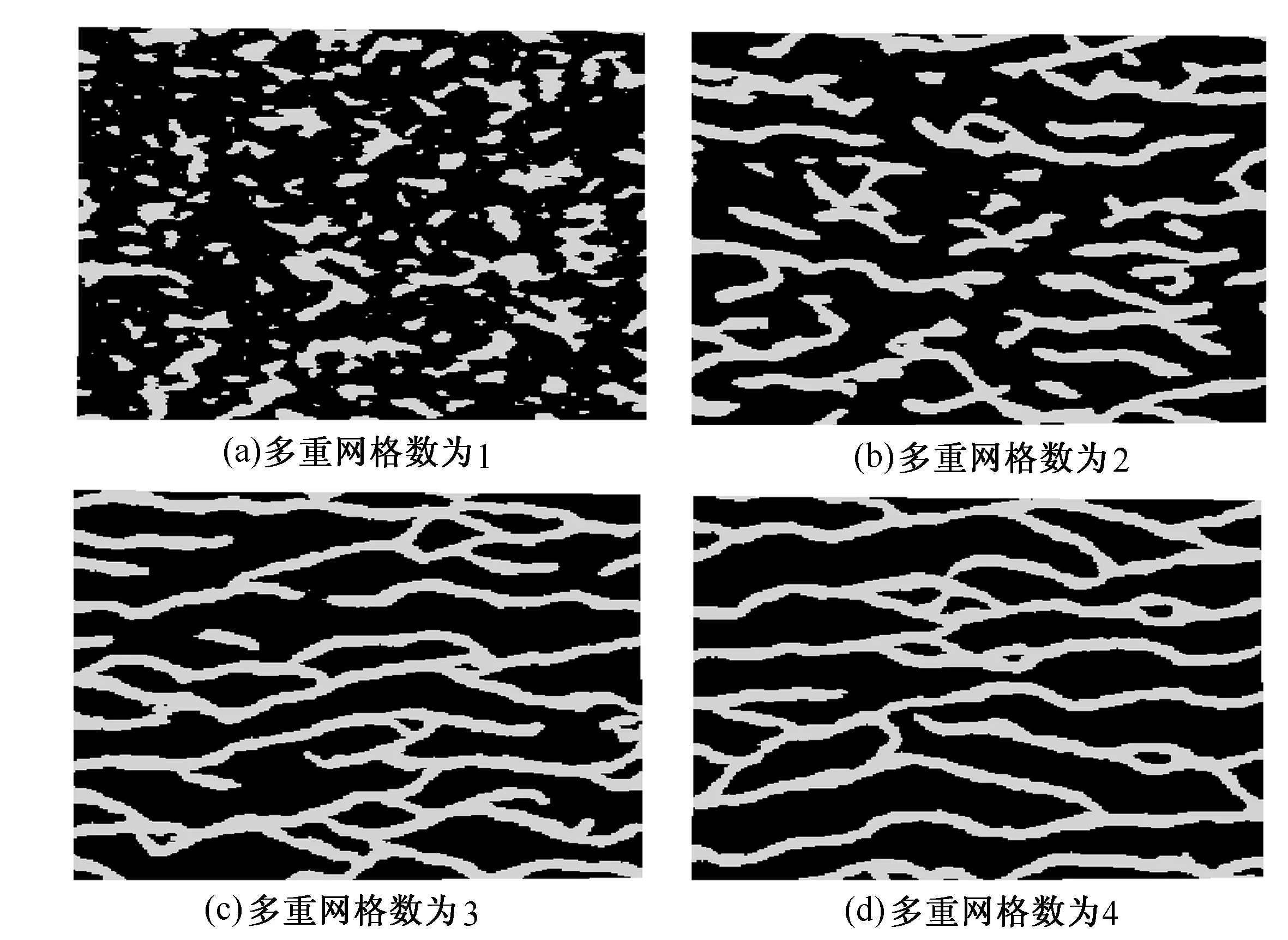
在保证训练图像平稳的条件下，当多重网格数为1时，数据模板不能够捕获较大范围的构造形态，河道形态极不明显，模拟结果很差(见图4(a))。多重网格数增加到2、3、4时，数据模板能够捕获较大范围的构造形态，河道形态逐渐变好，其中当多重网格数取3、4时，河道形态十分明显(分别见图4(b)、(c)、(d))。因此，多重网格数的选择以3、4为宜。

3 结 论

(1)多点地质统计学能够较好地描述几何形状较复杂的河道砂体等的连续性和变异性。

(2)当多重网格数确定时，最后一重模板不宜取较大值。

(3)当使用多重网格模拟时，多重网格数的选择以3、4为宜。

[1]王家华.迎接油气储层建模理论、应用大发展——从2007年估计石油地质统计大会谈起[J].地学前缘，2008，15(1)：16-25.

[2]尹艳树，吴胜和.储层随机建模研究进展[J].天然气地球科学，2006，17(2)：210-217.

[3]Ardiano F,Srivastava R M.Multivariate geostatistics:beyond bivariatemoments,geostatis-troia[J].Kluwer Publications,Dordrecht,1993，45:113-114.

[4] Strebelle S,Journel A G.Reservoir modeling using multi-point statistics[J].SPE71324,2001.

[5]Zhang T F.Filter-based training pattern classification for spatial simulation[D].California:Stanford University,2006.

[6]张挺，卢德唐，李道伦.基于二维图像和多点统计方法的多孔介质三维重构研究[J].中国科学技术大学学报，2010,40(3)：271-277.

[7]Strebelle S.Sequential simulation drawing structures from training images[D].California:Stanford University,2000.

[8]Strebelle S.Conditional simulation of complex geological structures using multi-point statistics[J].Mathematical Geology,2002,34(1):1-11.

[9]Tran T.Improving variogram reproduction on dense simulation grids[J].Computers and Geosciences,1994,20(7):1161-1168.

[10]汪彦龙，刘金华，边文莉，等.基于MPS和多重模板的孔隙介质重构方法[J].计算机仿真，2011,28(4):238-241.

2013-06-12

王家华(1945-)，男，教授，现主要从事储层地质建模、油藏描述、地质统计学等方面的教学与研究工作。

TE121.15

A

1673-1409(2013)26-0056-02

[编辑] 李启栋