双馈风力发电机的非线性PID功率控制

潘光辉，张 淼，黎庆发，李思琪，罗 芳

(广东工业大学，广东广州 510006)

0 引 言

双馈异步发电机(以下简称DFIG)，具有灵活调节有功无功功率、提供变速运行、实现最大风能捕获、减小机械应力、提高电能质量等优点，而且其变流器只需传输额定功率25%～30%的滑差功率，容量小、成本低，因此在大功率风力发电中得到广泛应用。

功率控制算法是DFIG风力发电机组控制中的关键问题。传统的DFIG功率控制常常采用基于定子磁链定向或者定子电压定向的矢量控制，这种方法主要取决于精确的电机参数，而电机参数如定子电阻、转子电阻、电感在电机运行过程中常常发生变化，导致控制系统的不稳定。本文在此基础上提出了直接功率控制，它是通过控制转子磁链的大小和相位，直接对输出的有功无功进行调控，可简化控制器结构，实现低谐波干扰，且对电机参数鲁棒性强，比矢量控制、直接转矩控制这两种控制方法控制效率高。

目前工程界中用于实际控制的控制算法仍以PI居多，传统的PI控制器参数固定不变，调节麻烦，影响了控制系统的使用范围，难以获得理想的实验结果。本文在传统PI的基础上，利用跟踪微分器对参考输入安排过渡过程，采用适当的非线性组合，提出新型的非线性PID控制算法，仿真结果表明，与传统直接功率控制相比，本文提出的基于非线性PID的直接功率控制对系统电机参数不敏感，提高了系统的鲁棒性，而且能有效地解决快速性与超调量之间的矛盾，减小动态过程中有功和无功功率的相互影响，使系统动态性能得到了进一步提高。本文的第二部分详细介绍了DFIG的数学模型，第三部分给出了基于非线性PID的控制器设计，第四部分给出了2.2 kW DFIG的仿真结果对比，第五部分给出了实验结果和结论揭示。

1 DFIG的数学模型

DFIG在转子dq坐标系中的定转子电压方程:

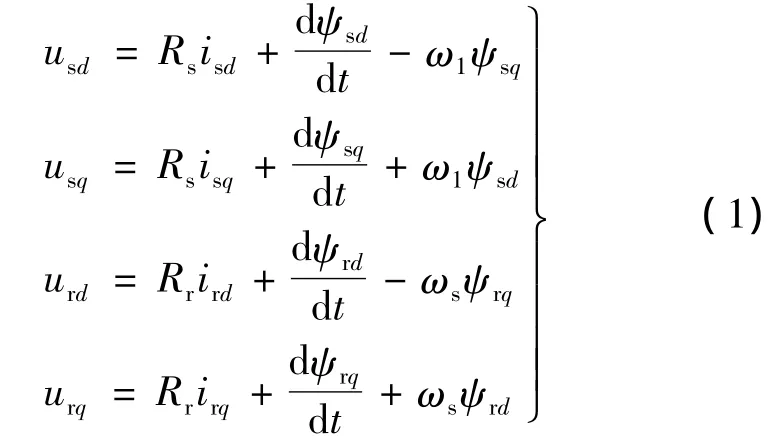
DFIG的磁链方程:

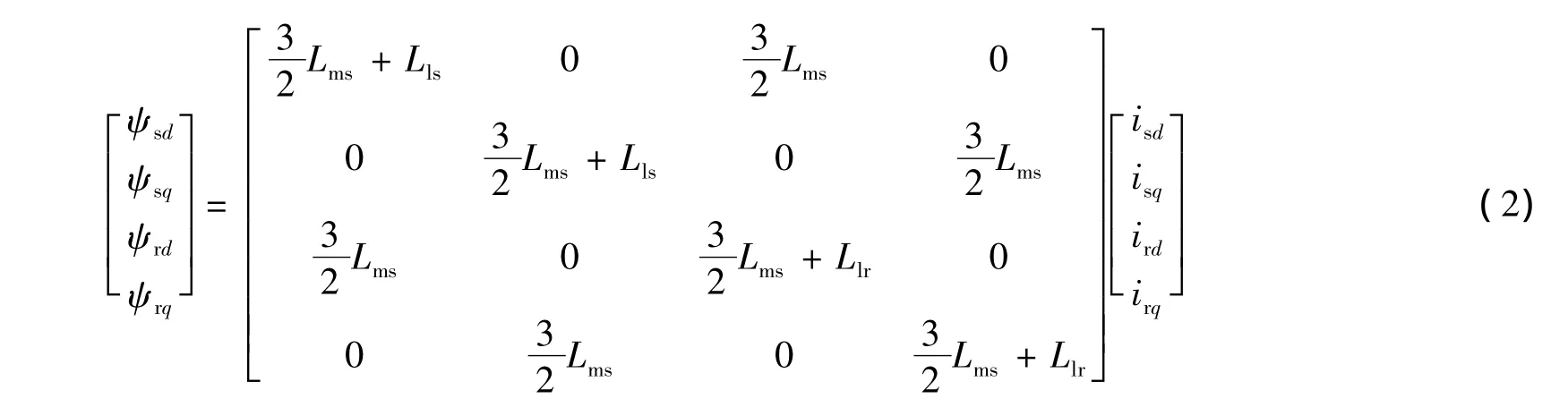
式中:u为电压;i为电流;ψ为磁链;R为电阻，下标d和q分别表示旋转坐标系的d轴和q轴，下标s和r分别表示定子绕组和转子绕组;ωl为定子频率同步角速度;ω为转子转速;ωs为dq轴相对于转子角速度，ωs=ωl－ω。

采用定子磁场定向的直接功率控制方法，将同步坐标系的d轴与定子磁链重合，忽略定子绕组电阻压降，则定子侧电压落在同步轴系q轴上，与定子磁链相差90°。

把式(3)、式(4)代入式(1)得到并网后定子电压方程:

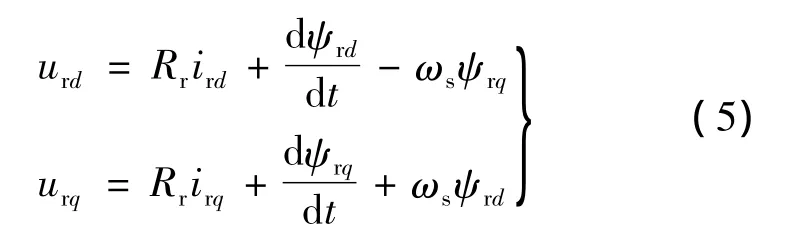
联立式(2)、式(5)，得到定子输出到电网的有功功率和无功功率:

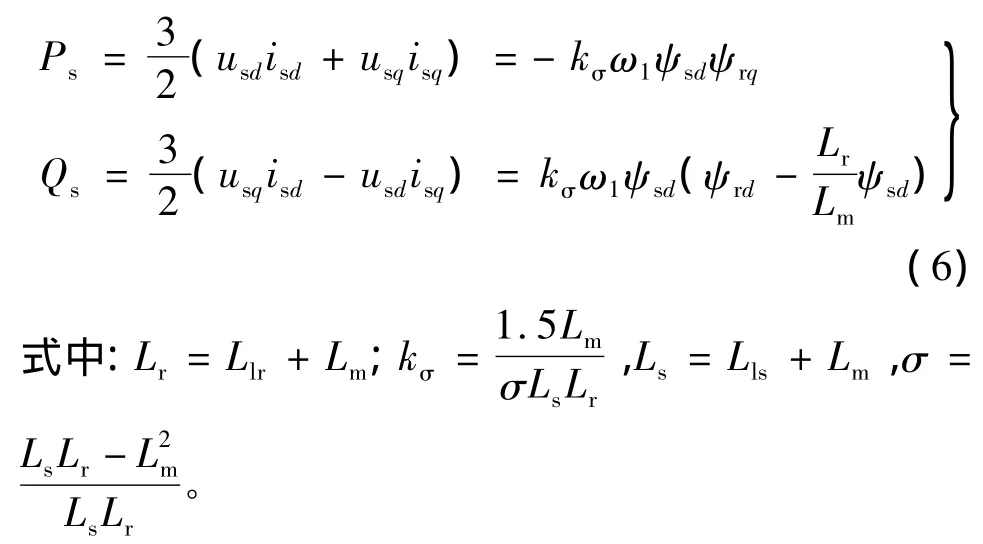
忽略转子电阻，得到转子电压在dq轴上的分量:

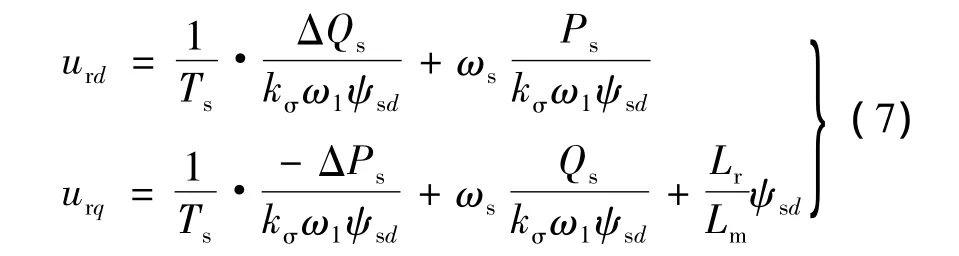
2 控制器的设计

2.1 跟踪－微分器(TD)

跟踪微分器是由韩京清提出的提取微分信号的方法，它是将输入信号v(t)转换为两路信号，一路为过渡过程信号v1，v1跟踪v(t)，另一路变化趋势信号v2，v2=，把v2作为v(t)的“近似微分”。其作用是根据给定输入v(t)和受控对象来安排过渡过程，提出此过渡过程的导数并得到光滑的输入信号。

跟踪微分器离散化的数学表达式:

fhan(v1，v2，r，h)为如下定义的非线性函数:

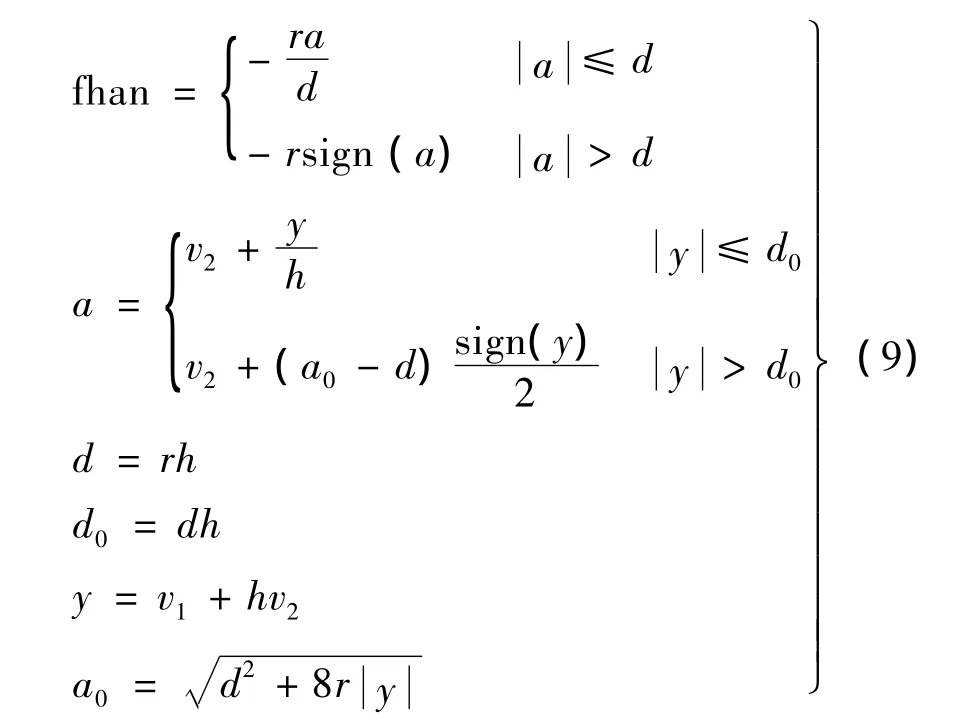
式中:v(t)为输入信号;T为积分步长;r是反映跟踪速度快慢的因子，r越大跟踪速度越快，但会放大噪声污染;h是跟踪微分器的滤波因子，扩大滤波因子是增强滤波效果的有效手段，但h越大会使跟踪信号的相位损失越大。这里取r=200，h取适当大于步长 T 的值，即 h=0.3，T=0.1，既可以抑制微分信号中的噪声放大，又可以消除功率跟踪中的超调现象。

2.2 非线性控制器

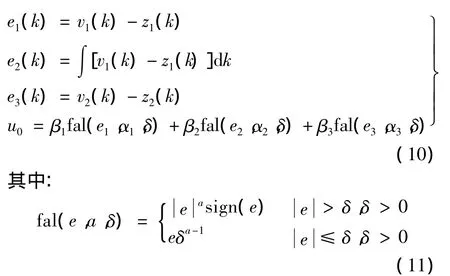
系统的状态误差是指e1=v1－z1，e2=∫(v1－z1)dk，e3=v2－ z2，v1、v2是给定信号的跟踪值和近视微分，z1、z2是反馈信号的跟踪值和反馈值。根据误差e1、e2、e3的非线性组合来决定控制量u0。当0＜α＜1时，fal是非线性非光滑的误差反馈率，具有小误差大增益、大误差小增益的特点;当α＞1时，fal是非线性光滑误差反馈率，具有小误差小增益、大误差大增益的特点。由比例、积分、微分各自所要发挥的功效和fal函数的特性，对于比例，取0＜α1＜1 ，对于积分，取 α2＞1 ，对于微分，取0＜ α3＜1，这里取 α1=0.75，α2=1.5，α3=0.1。根据现场的运行经验，选择 δ=100，β1、β2、β3为可调参数，这里取 β1=0.001，β2=0.1，β3=1.5，可以实现系统对动态特性和稳定性的要求。

系统的原理框图如图1所示。

3 仿真对比验证

本文应用MATLAB 2009a在Simulink中分别对传统直接功率控制和基于非线性PID的直接功率控制进行仿真研究。仿真模型中双馈电机参数如下:额定电压380 V，额定功率2.2 kW，额定频率50 Hz，同步转速1500 r/min，离散时间积分步长0.2 ms，定子电阻 2.6497 Ω，转子电阻 5.8765 Ω，定子电感0.0178 H，转子电感0.0178 H，定转子间互感0.2947 H，转动惯量 0.068 kg·m2，其中经典 PI调节参数整定:比例系数 kp1=0.01，kp2=0.001，积分系数 ki1=0.8，ki2=0.5;非线性 PID 的参数整定:比例系数 kp1=0.001，kp2=0.001，积分系数 ki1=0.1，ki2=0.1，微分系数 kd1=1.5，kd2=1，r=200，h=0.3，T=0.1。

双馈电机并网发电后，一开始有功和无功功率给定为零。在1 s时刻给定－700 W有功功率阶跃，3 s时刻给定800 Var的无功功率阶跃，进行传统直接功率控制和基于非线性PID直接功率控制的仿真结果对比。

由图2、图3仿真结果可知，基于非线性PID的直接功率控制能减少时滞，避免振荡并快速无超调的跟踪给定阶跃。由图4可知，基于非线性PID的直接功率控制能够减少无功功率对有功功率的影响。由图6可知，在有功功率没有超调的情况下，基于非线性PID直接功率控制的定子电流跟踪速度明显快于传统直接功率控制，具有更好的动态性能，由图7可知，相比传统直接功率控制，基于非线性PID的直接功率控制在跟踪有功功率时，有相位超前的功能。

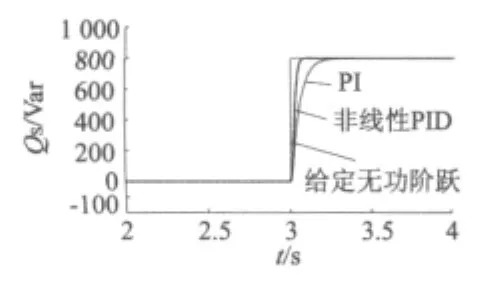
图3 给定800 Var的无功功率阶跃

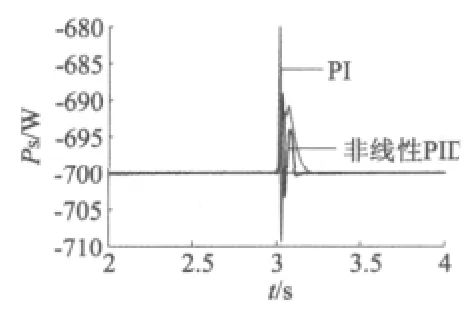
图4 无功对有功的影响

图5 定子A相电压

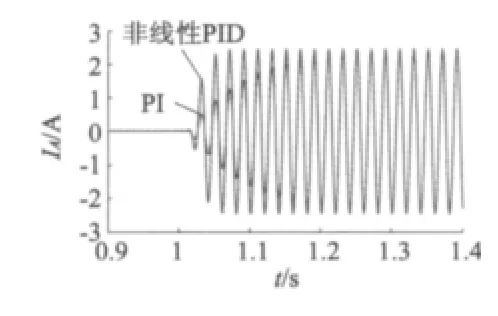
图6 定子A相电流

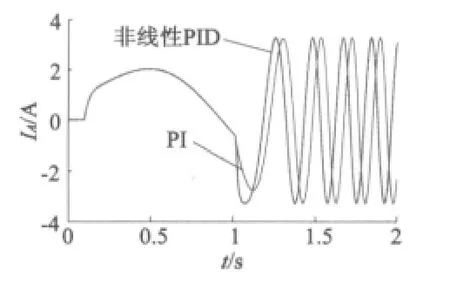
图7 转子A相电流

4 实验波形与结论

用4 kW、380 V、1440 r/min的三相异步电动机模拟风机带动双馈电机转动，转子励磁装置由两个背靠背的双相变流器和一个2400 μF的直流电容组成，变流器的功率是5.5 kW，IGBT的开关频率是10 kHz，控制芯片采用TI公司的 TMS320F2808，它是12位A/D转换器，16路通道。采用兵字的霍尔传感器采样电流电压，采样频率为500 μs，用QEB电路测定经过光耦隔离的编码器脉冲数来计算转速。在仿真的数据条件下，得到基于非线性PID的DFIG直接功率控制实验波形。

图8是网侧起动时的直流母线电压波形，图9是电网电压和与电网电压同频同相同幅的定子电压波形，图10是给定有功－700 W和无功800 Var时的定子电流波形，图11是给定无功800 Var时的定子电流波形，相位前移，图12是并网后给定有功－700 W和无功800 Var时的转子电流波形，提供转差频率。

本文详细论述了基于非线性PID的直接功率控制策略及实现方法，并对传统直接功率控制和基于非线性PID的DFIG直接功率控制进行了仿真结果对比研究。仿真结果表明基于非线性PID的直接功率控制系统参数适用范围广，能够较大程度地削弱电机参数变化和负载突变对系统造成的扰动，具有良好的鲁棒性，而且能快速稳定地跟踪响应，超调量小，实验结果也证明了这种算法的正确性。

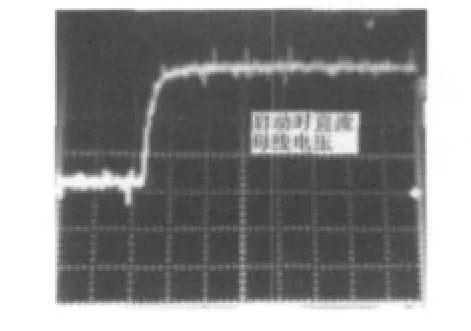
图8 直流母线电压

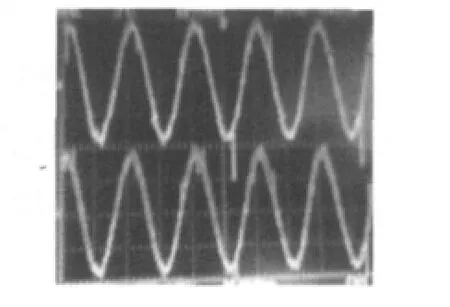
图9 电网电压和定子电压

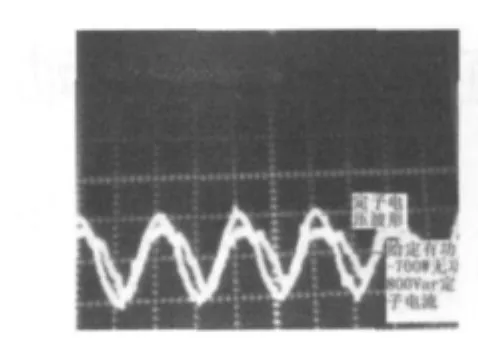
图10 定子电压和定子电流

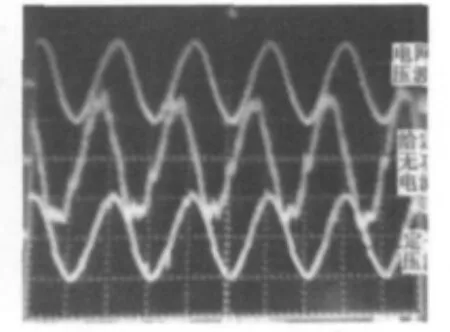
图11 定子电流

图12 转子电流

［1］韩京清.非线性PID控制器［J］.自动化学报，1994，20(4):487－490.

［2］梅柏杉.直接转矩控制系统中定子电阻的影响分析［J］.微特电机，2009，16(4):13 －15.

［3］Zhi D，Xu L.Direct power control of DFIG with constant switching frequency and improved transient performance［J］.IEEE Transactions on Energy Conversion，2007，22(1):110 －118.

［4］潘卫明.新型直接功率控制算法在双馈风电平台的应用［J］.电力电子技术，2010，44(6):10 －13.

［5］张淼，吴捷.基于自抗扰技术的光伏发电并网控制系统［J］.控制理论与应用，2005，22(4):583－587.

［6］Kim Won － Sang.Direct power control of a doubly fed induction generator with a fixed switching frequency［J］.IEEE Transactions on Energy Conversion，2008，11(1):1 －9.

［7］刘吉宏.基于非线性PID的双馈发电机有功功率控制［J］.华东电力，2009，37(11):1922 －1924.

［8］张明.非线性 PID控制在液位控制系统中的应用［J］.工业控制计算机，2008(2):30.