三自由度混合磁力轴承数字控制器的设计

华 春，邓智泉，刘程子，邢绍邦

(南京航空航天大学，江苏南京 210016)

0 引 言

磁力轴承利用磁场力将转子无接触地悬浮于空间，具有无机械磨损、无需润滑、维护成本低、使用寿命长等优点，在超高速超精密加工、航空航天、交通和能源等高科技领域有广阔的应用前景［1］。而在航空航天这一特殊领域，对磁力轴承的重量、体积和功耗有着更高的要求。混合磁力轴承［2］利用永磁体和控制线圈产生的磁场维持转子的悬浮，与主动磁力轴承［3］相比，各空间自由度省去一组线圈和功放，减小了体积和重量，降低了功耗，与被动磁力轴承［4］相比，可实现全自由度悬浮且动态性能好，因此更加适应航空航天的应用要求。混合磁力轴承设计的关键问题是控制系统的设计，控制系统的性能决定了磁力轴承的悬浮质量。传统模拟控制器虽然在一定程度上满足了磁力轴承的工作要求，但存在参数调整不方便，硬件结构不易改变，难以实现先进的控制算法元器件老化等问题［5－7］。本文以DSP TMS320F2812［8］芯片为核心，基于一种轴向－径向三自由度混合磁力轴承，设计了一套数字控制系统，并从提高磁力轴承性能、可靠性等角度出发，采用变参数PID控制策略，实现了数控磁力轴承的稳定运行。

1 三自由度混合磁力轴承

1.1 三自由度混合磁轴承的结构及工作原理

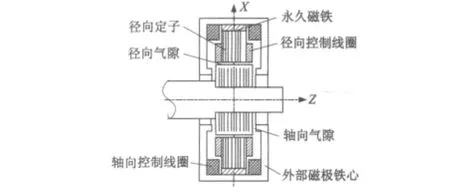
图1 三自由度混合磁力轴承

图1为永磁偏置轴向径向磁力轴承的结构示意图，它由永久磁铁、径向定子、径向控制线圈、外部磁极铁心(轴向定子)、轴向控制线圈等构成。环形永磁体采用径向充磁，产生的偏置磁通由外部磁极铁心、轴向气隙、转子、径向气隙、径向磁极路径完成闭合，如图2中实线所示。各个自由度的两组控制线圈串联连接，产生的控制磁场极性相同，图2(a)中虚线为轴向控制磁通的闭合路径。当转子轴向受力向右运动时，位移传感器检测出z方向转子位移，在控制绕组中通以电流，产生磁通方向与左边气隙处偏置磁通方向相同，与右边相反，继而对转子产生向左的磁拉力，将转子拉回平衡位置。径向x、y悬浮机理与轴向相同，图2(b)为径向y发生偏移时磁场情况。

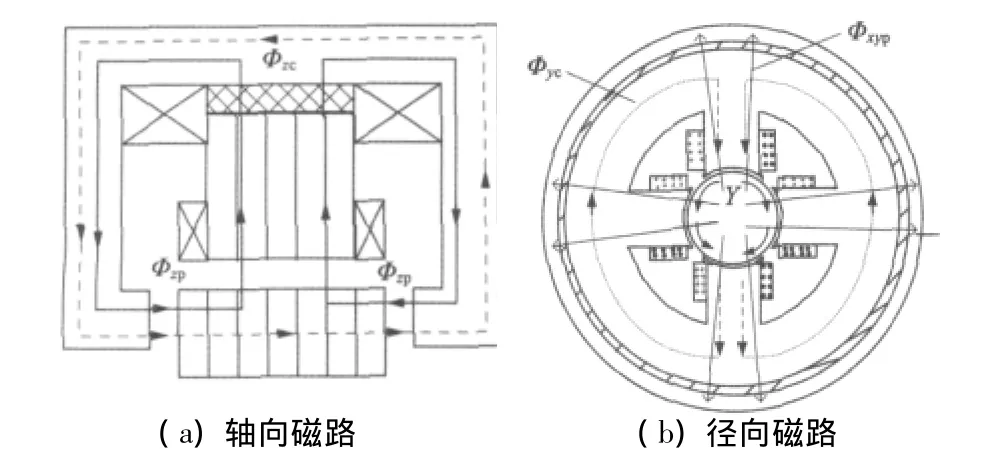
图2 三自由度混合磁力轴承磁路

1.2 三自由度混合磁力轴承数学模型

由图2中磁场路径可知，轴向、径向的偏置磁通路径耦合，但控制磁路相互独立，并且控制磁通基本不通过永磁环，这种磁路结构保证了在平衡位置附近轴向力和径向力的相互解耦［9］，因此磁力轴承的各自由度数学模型可分别建立，下面以轴向为例，表述单自由度的数学模型。在平衡位置附近，转子轴向发生很小的位移时，悬浮力可表示:

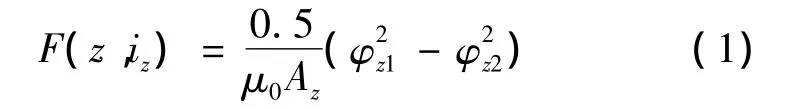
式中:φz1和φz2分别为轴向气隙处磁通，是z和iz的函数，z为转子偏离平衡位置的距离，iz为轴向控制电流;Az为轴向磁极面积。利用等效磁路法对该磁力轴承进行分析，可得到φz1和φz2的函数表达式，将式(1)在z=0、iz=0处进行泰勒展开，并且忽略二阶导数以上的高次项，可得［9］:

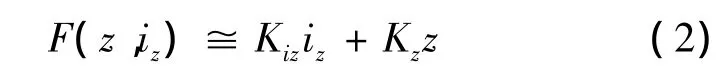
式中:Kiz和Kz分别为电流刚度系数与位移刚度系数，大小由磁力轴承结构参数决定。

根据力学定律，得:

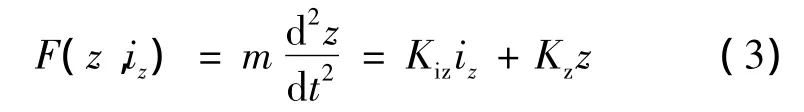
式中:m为转子质量。

将上式经Laplace变换，得到磁力轴承轴向数学模型:

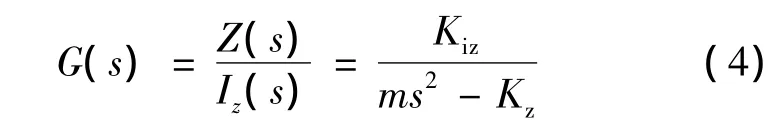
同理可推导出径向磁悬浮力和数学模型表达式。

2 硬件电路设计

如图3所示，磁力轴承数字控制系统主要包括位移传感器、数字控制器和功放电路。位移传感器检测转子位移，在数字控制器中运算得到所需电流信号，通过功放电路放大，在电磁线圈中产生控制电流，从而产生磁拉力将转子拉回平衡位置。

图3 磁力轴承控制系统

本文磁力轴承的轴向与径向气隙均为0.5 mm，所以在保证较高的灵敏度前提下，位移传感器的线性测量范围需大于1 mm。选用瑞视公司的RS9000XL系列5 mm电涡流传感器，其线性量程为2 mm，线性起始点0.6 mm，线性误差±1%，采用－24 V供电，输出范围为0～－20 V，测量精度16 V/mm。

数字控制器主要由ADC、DSP和DAC组成，给定位移信号与实际位移做差后经调理电路整定为ADC芯片可接收的电压信号，在DSP中按照预定的控制算法进行运算，然后通过DAC芯片将数字信号转化为模拟电压信号输出至功放电路。本文选用TI公司的 DSP芯片 TMS320F2812，最高主频达到150 MHz，指令周期仅为6.67ns，并且内部集成了16通道的12位ADC，故无需再外扩ADC，使得硬件电路更简洁。D/A转换电路选用Maxim公司的Max527，它是8路13位电压输出型数模转换器，采用±5 V供电。数据通过两次写操作装入各寄存器，并通过异步装载DAC输入信号将输入寄存器数据装入DAC寄存器，建立时间为5 μs。

为保证转子的平稳起浮和稳定旋转，功放电路需具备较宽的通频带和良好的响应特性。本文选择普遍采用的单相全桥开关功放，并运用改进型采样－保持策略［10］，当实际电流跟踪上给定电流，误差极性信号发生偏转，单相全桥进入续流状态，大大降低了电流纹波和开关损耗。

3 软件程序设计

3.1 控制软件结构

控制程序由主程序和中断子程序组成。如图4所示，主程序执行时首先进行系统及外设初始化设定，然后开通用定时器1并循环等待中断事件。通用定时器1周期匹配时中断事件发生，DSP响应中断，并执行中断服务子程序。中断程序执行时首先调用三路AD采样结果并进行滤波，然后根据控制方法对采样结果运算，并且根据_IQmath函数和Max527数模转换规律对结果进行限幅，最后通过数模转换语句输出。中断子程序执行完成后返回主程序，继续循环等待。

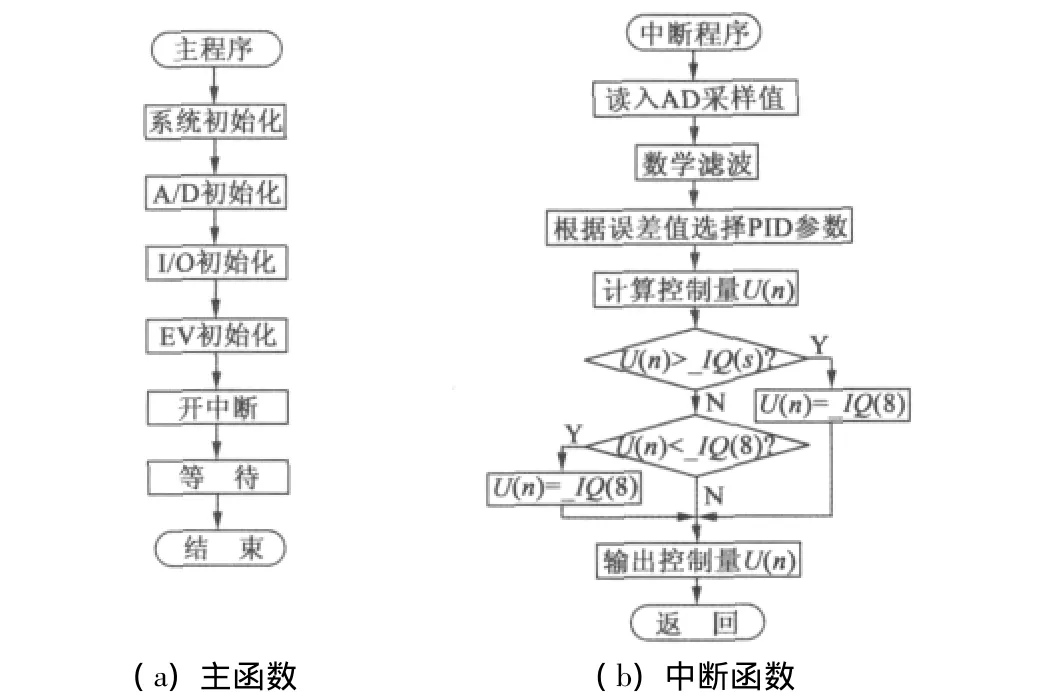
图4 程序流程图

3.2 控制算法

PID(比例－积分－微分)控制是在长期工程实践中总结出来的一种控制方法，其参数整定方便，结构改变灵活，在控制理论中技术成熟且较为常用。

比例系数Kp决定响应速度，Kp越大，响应越快，调节时间越短，但Kp过大，系统稳定性变差;积分时间常数Ti决定稳态误差，Ti越小，偏差越小，但同时系统动态响应越慢，在偏差较大时易引起积分饱和;微分环节根据偏差变化趋势做出反应，微分时间常数Td越大，系统超调越小，但同时系统更易受到高频干扰的影响。

为克服传统PID算法中微分突变和积分饱和问题，本文采用不完全微分和积分分离控制算法，偏差较大时采用PD控制，较小时采用PID控制，同时微分后串联高频滤波环节，其数学算式:

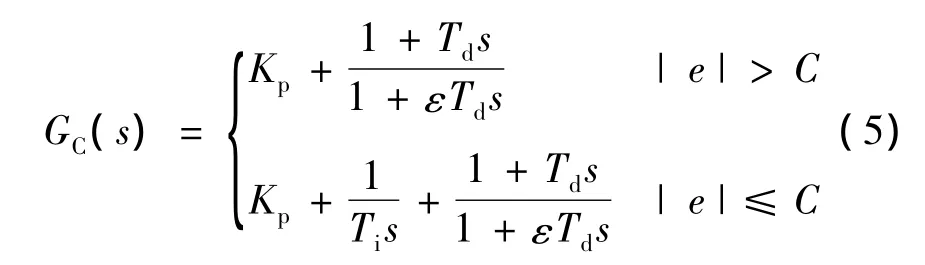
然而，由于混合磁力轴承控制系统结构复杂，难以建立精确的数学模型，特别是在系统起浮阶段，非线性严重，所以采用一组固定的参数往往难以获得较好的控制效果。

针对上述问题，本文以不完全微分和积分分离为基础，采用多区间变参数PID算法。Kp在偏差较大时取较大值，较小时取较小值，这样同时保证了系统的响应速度和稳态性能;Ti在偏差较大时取较大值，较小时取较小值，这样系统稳态误差小且不易引起积分饱和;Td在偏差较大时取较小值，较小时取较大值，这样有利于加快系统对小偏差的反应速度，又因采用不完全微分算法，所以不易受到高频干扰［11］。数学算式:

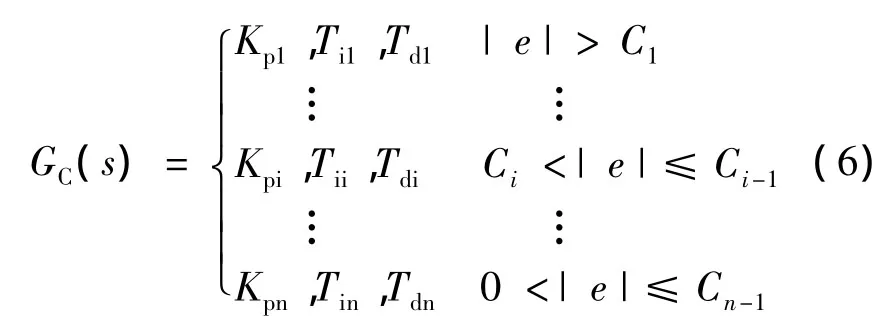
4 仿 真

本系统永磁体选择钕铁硼N35，轴向与径向线圈均为单股100匝，转子质量为3.5kg，磁力轴承结构参数如表1所示。

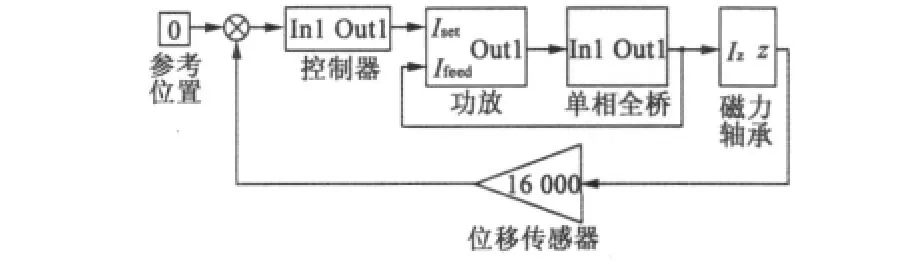
图5 仿真模型

根据式(1)～式(4)计算轴向模型:

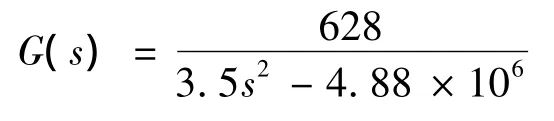
径向模型:

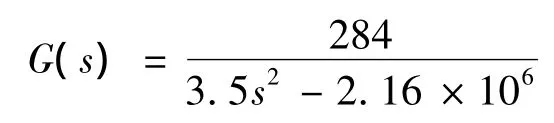
以轴向为例，在MATLAB/Simulink环境下搭建仿真模型，如图5所示。给定位移为0，设置转子初始位置为0.3 mm(对应实际系统中保护轴承的气隙宽度);位移传感器视为线性传输，放大系数为16000;控制器分别采用基于不完全微分和积分分离的定参数和变参数PID策略;功率放大器模型根据单相全桥改进型三态采样保持策略搭建，与实际系统较为接近;磁力轴承物理模型较为复杂，用本文计算得到的线性数学传递函数代替。

根据PID各环节对系统响应的影响，多次仿真得出一组较优的PID参数，如表2所示。分别采用定参数和变参数PID控制方法，转子响应曲线如图6所示。由仿真结果可以看出，变参数控制不论是上升时间、调节时间，还是超调量都优于定参数PID控制。

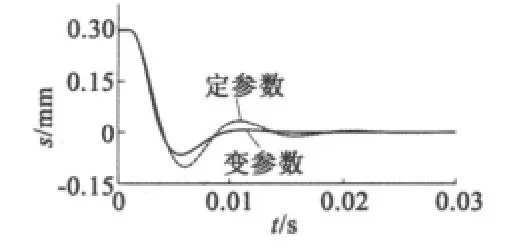
图6 转子起浮响应曲线

表2 仿真参数

5 实 验

本文以开关磁阻电动机转轴为支承对象，两端均采用三自由度混合磁力轴承，运用变参数控制算法，设计并制作了一套数字控制系统，如图7所示。

图7 混合磁力轴承及其控制系统

调节控制参数，实现磁力轴承系统的稳定悬浮，图8是系统稳定悬浮时的位移曲线波形。

由图8可知，转子稳定时，轴向与径向振动位移均在±5 μm以内，稳态悬浮精度较高。图9是系统起浮时的位移曲线，可以看出，轴向与径向起浮时间1.5 s，系统起浮时间较短。图10是系统受扰动时的位移曲线，图10(a)中轴向振动最大为400 μm时，30 ms恢复稳定，图10(b)中径向y最大振动为180 μm时，100 ms内重新稳定，并且径向x几乎无振动，表明系统抗干扰能力较强。

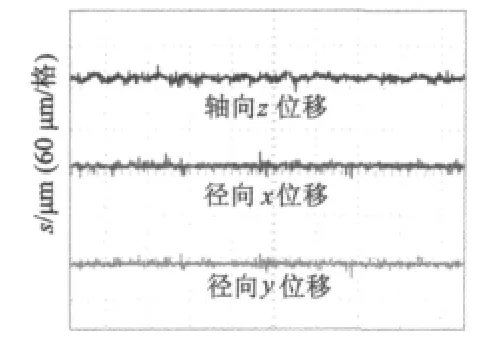
图8 转子稳定悬浮位移曲线

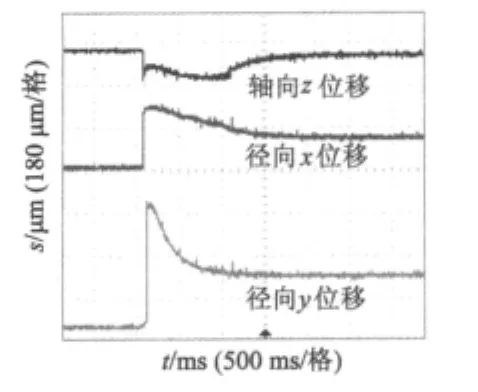
图9 转子起浮位移曲线

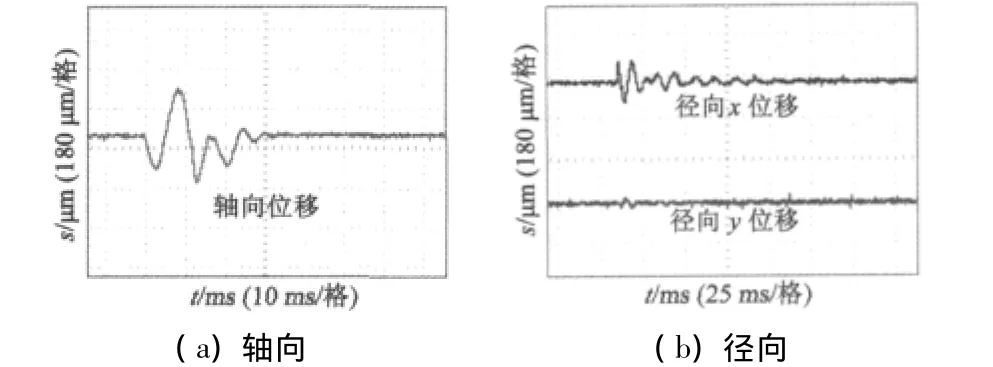
图10 转子受扰动位移曲线

6 结 语

三自由度混合磁力轴承体积小、重量轻、功耗小、承载力大，在航空航天领域有较好的应用前景。以TMS320F2812为核心的数字控制器硬件电路简单，能减缓元件老化问题，并且可实现复杂的控制算法，从而提升磁力轴承的动态性能。变参数PID控制算法可实现磁力轴承系统的稳定悬浮，且与传统PID控制比较具有响应速度快、超调小、噪声低、刚度大和控制精度高的特点，有利于磁力轴承的推广和应用。

［1］胡业发，周祖德，江征风.磁力轴承的基础理论与应用［M］.北京:机械工业出版社，2006.

［2］赵旭升，邓智泉，王晓琳，等.永磁偏置磁轴承的研究现状及其发展［J］.电工技术学报，2009，29(9):9 －20.

［3］Schweiter G，Bleuler H，Traxler A.Active magnetic bearings－basics，properties and application of active magnetic bearings［M］.ETH，Switzerland，1994.

［4］Yonnet J P.Permanent magnets bearings and couplings［J］.IEEE Trans.Magnetic，1981，17(2):1169 －1175.

［5］罗诗旭，汪希平，杨新洲.基于DSP的磁悬浮轴承数字控制系统设计［J］.电子技术，2003(1):6－9.

［6］Williams R D，Keith F J，Allaire P E.Digital control of active magnetic bearings［J］.IEEE Transactions on Industrial Electronics，1990，37(1):19 －27.

［7］Hung J Y，Albritton N G，Xia Fan.Nonlinear control of a magnetic bearing system［J］.Mechatronics，2003，13(6):621 － 637.

［8］TI.TMS320F2812 Datasheet(SPRS174)［M］.Texas Instruments，2003.

［9］李冰，邓智泉，严仰光.一种新颖的永磁偏置三自由度磁轴承［J］.南京航空航天大学学报，2003，35(1):81 －85.

［10］臧晓敏，王晓琳，仇志坚，等.一种改进的基于采样保持策略磁轴承用三态调制开关功放［J］.电工技术学报，2004，19(10):85－90.

［11］Wu Qinghai，Ni Wei，Zhang Tao，et al.Study on digital control system of AC 2－degree freedom HMB based on parameter automatic self－ adjustment Fuzzy PID［C］//The 2nd International Conference on Intelligent Control and Information Processing.2011:1098－1101.