一种改进的混沌直扩方案

兰 楷，王亚涛

（中国电子科技集团第十研究所，四川 成都 610036）

0 引言

直接序列扩频通信采用“隐蔽”策略，其发射功率谱很低，通常可以淹没在噪声之中从而很难被发现，具有低截获概率特性，在军事通信中得到了广泛应用[1]。

传统的直扩通信采用二进制伪随机序列作为扩频码来扩展原始信号的频谱和作为用户地址码，如m序列和Gold序列等。但他们都在不同程度上存在着数量有限、复杂度低、抗截获性能差等缺陷。混沌序列凭借其初值敏感性，容易产生数量众多且具有良好相关性能的伪随机序列，从而代替传统扩频码受到了广泛研究。文献[2-4]证实这种替代的可行性。

与之对应，非协作方针对直扩信号的盲检测、盲估计和盲解扩的研究也广泛开展，其中最主要的是循环谱理论[5-7]。文献[5]应用循环谱理论实现了对直扩信号的盲检测并且对直扩信号载频、伪码速率、伪码周期成功进行了估计。大量文献更是针对这 3个参数估计提出了各种改进方法。

综上分析，为进一步提高直扩信号的LPI性能，在混沌扩频的基础上，文中提出了一种改进方案，使用不定长的扩频码，快速地改变混沌扩频的通信速率，从而获取更高的低截获性能。

1 混沌直扩系统理论分析

1.1 直扩系统模型

由文献[8]可知，直接序列扩频就是用高速率的伪随机码序列与信息码序列模二加后产生的复合码序列去调制载波。

以BPSK为例，假设 d(t)为原始信号，c(t)为扩频码，取值均为±1，则模二加等效为两序列相乘，故复合序列为d(t)· c(t)；A为载波幅度，f0为载波频率。这样，发射机的射频输出发射信号为:

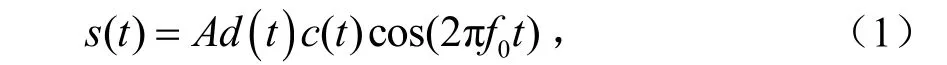
可等效为一个振幅只取±A的二值正弦波形，是一个抑制了载波后的幅度调制信号。

在接收端，用与发射端同步的本地参考扩频码cR(t-)与接收信号相乘进行相关解扩。设传输时延为Td，当扩频码取得同步后，则有c(t-Td)·cR(t-)=1。接下来，通过进一步解调，就可以恢复出原始信号。

1.2 混沌直扩

所谓混沌直扩，指的是采用混沌序列作为扩频码的直扩系统。混沌扩频序列的相关特性与随机二进制序列非常相似，其自相关函数为δ函数，而互相关函数近似为0。加上其本身的初值敏感性，同过一个混沌映射模型，即能产生大量互不相关的扩频码序列。经典混沌扩频序列有4种:

（1）Logistic映射:

式中，3.56994μ＜…≤，为分形参数。

（2）改进型Logistic映射:

（3）Tent映射:

式中，ρ为阶数。

通常，采用二值量化法得到具体的数字混沌序列，通过设置一个门限，门限值以上的量化为“1”，否则量化为“-1”。例如，可以将迭代序列的均值作为门限值。还可以按照伪随即码的具体指标参数进行序列优选，得到更高性能的混沌序列。

2 改进方案简介

传统的扩频通信系统中，每个信息比特所包含的扩频码位数是一个定值，在原始信号速率不变的情况，扩频信号的速率固定不变。固定码长的扩频码表征了其周期性，说明了直扩信号是一个周期平稳过程。常用的循环谱密度法估计载频以及伪码速率都是基于这样的一个基本事实。

混沌序列本身就是非周期的，长度无限，混沌序列应用于直扩系统是通过对序列的截短实现的。

方式一:保持混沌序列的非周期性，设定速率切换的信息位数M以及第m次变速后扩频码的长度Nm，信息比特x(k)由c(n)表示，其中:

第0次变速，即未变速时，式中没有乘积项。()M表示对M取余。可见，此时的每个信息比特所包含的扩频码序列是不同的，并且扩频码的速率在不断变化，即序列的截短长度在每隔一定位数M·Nm后发生变化，这样非常有利于掩蔽信息。

方式二:将混沌序列设置成周期可变的周期性序列。这里设置可变周期时有两种方法，一是在每次变速时，设定该速率下序列的截短长度Nm，每产生Nm位扩频码后初始化序列发生器；二是在变速前，存储第Nm位扩频码的序列值，将这个值作为初始化的值，其余同一。

3 仿真分析

采用MATLAB工具进行仿真，仿真对象为改进型Logistic混沌序列。以下为其伪随机特性仿真。

由图1可以看出，改进后的序列保持了混沌序列本身的初值敏感性，两序列初值相差仅为10-6，轨迹完全不相关。因此能产生大量不相关的混沌扩频序列。

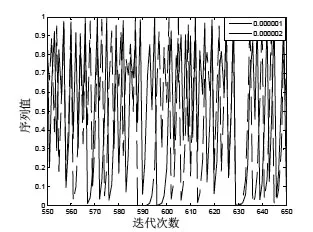
图1 初值相差10-6的两序列轨迹

由图2可以看出，序列长度超过50时，平衡度值已经低于0.1，之后曲线变化不明显，这为速率可变化的范围提供了依据。

由图3和图4可以看出，序列具有类似δ函数的尖锐特性，互相关函数值趋于0。由此可知，序列满足扩频码的伪随机特性要求，适合作为直扩系统的扩频码。

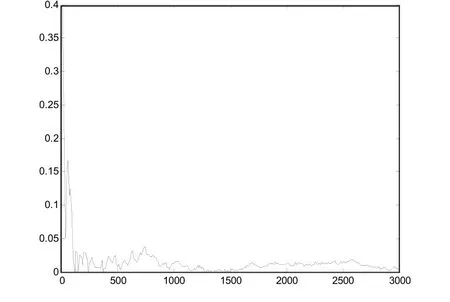
图2 平衡性随长度的变化关系

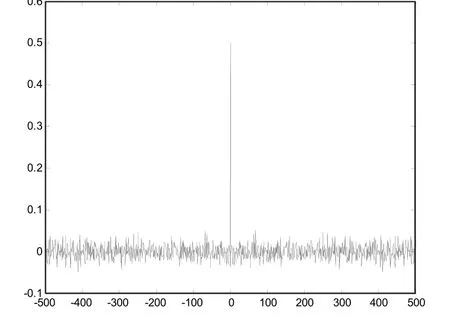
图3 自相关函数

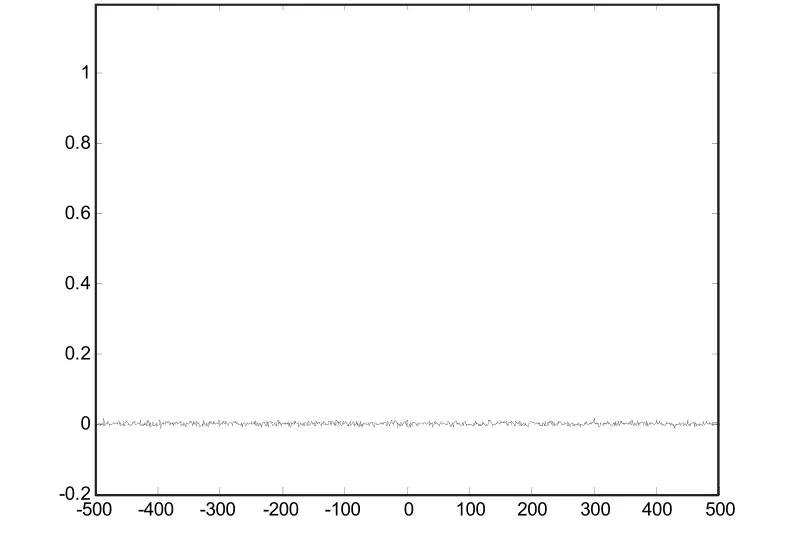
图4 互相关函数

对直扩信号的参数估计，大多基于直扩信号本身是一个周期平稳过程这样一个基本事实，其中以谱相关估计法为代表。而方案一的变速方式使得扩频码本身失去了其周期性，可以预见该类估计方法面对方案一波形将失效；而方案二虽然保持了多周期性，但由于在射频速率上参数估计的非实时性，通过设置合理的变速切换时间，可使其即使估计出参数也失去了通信截获的意义，从而是系统LPI性能提高。进一步的仿真验证将在后续论文中体现。

4 结语

文中从抗截获的对立面非协作方盲接收的参数估计出发，提出了一种基于改变扩频码长度的变速混沌扩频通信方案，通过仿真，验证了其良好的伪随机特性，分析了其抗参数估计的能力。与传统的直扩通信系统相比，这种方案具有更好抗截获性能。目前方案一以及方案二中第二种初始方法对扩频码的同步以及每帧信号的接收完整性要求极高，具体的工程应用还有待进一步研究。

[1]胡文江,徐潇潇,方磊.扩频技术及其应用[J].信息安全与通信保密,2006(08):168-170.

[2]王亥,胡健栋.Logistic-Map混沌扩频序列[J].电子学报,1997,25(01):19-23.

[3]王亥,胡健栋.改进型 Logistic-Map混沌扩频序列[J].通信学报,1997,18(08):71-77.

[4]黄乘顺,李星亮.基于混沌的扩频通信系统及性能分析[J].通信技术,2008,41(12):37-39.

[5]程皓.低截获直扩信号参数盲估计方法研究[D].成都:电子科技大学,2007:12-33.

[6]刘伟,杜娟.基于循环谱理论的弱信号检测及特征参数估计[J].通信技术,2010,43(04):28-30.

[7]杨敏军,邱玲.非协作通信中直扩信号检测[J].信息安全与通信保密,2007(02):86-87.

[8]田日才.扩频通信[M].北京:清华出版社,2007.