基于ECC和SHA-1电子印章文件校验实现

杨占民，曹 斌，闾凡兵，王鹏飞，国洪新

（①贵州大学 计算机科学与信息学院，贵州 贵阳 550025；②贵阳铝镁设计研究院，贵州 贵阳 550081；③贵州信安科技有限公司，贵州 贵阳 550002）

0 引言

二十世纪九十年代以来，网络技术快速发展，互联网已经渗透到我们的日常生活，从各方面改变着我们的生活。信息化的电子政务和电子商务已经成为世界各国政府政务和商业经营活动的一种新模式。为了保证在电子政务和电子商务交流的安全，需要采用一定的安全措施，此时电子印章被提出并广泛的应用[1]，然而电子印章的核心技术问题，是如何保证电子印章文件(以下用加印文件代替)的合法性。因为电子文件容易被复制、篡改，那么如何保证加印文件的完整性、合法性、安全性是电子政务和电子商务成功的关键，因此就要求加印文件必须具有防伪性、安全性[2]。所以为了解决以上问题，文中在电子印章系统的基础上，提出一种“基于ECC和SHA-1的加印文件校验方案及实现”通过相关的密码学知识，实现了加印文件不可否认、不可伪造及保证完整性。

1 基础知识

1.1 ECC签名及验证过程

椭圆密码体制ECC签名产生过程，假设用户A使用以下流程对消息M进行数字签名[3]，具体步骤如下:

验证过程:

假设验证方为B，B验证A签名，需要知道A的公钥 PA，那么B的验证流程如下:

1.2 散列函数

散列函数 SHA是一种数据加密算法。SHA-1是SHA家族中的一种，该算法的思想是输入一段数据明文，经过SHA之后输出160位密文，且这一过程是不可逆转的。输出值被称之为散列值或摘要，它与明文唯一对应。与哈希函数MD5相比较摘要更长，安全性也更高[4]。其单个循环过程如图1所示。

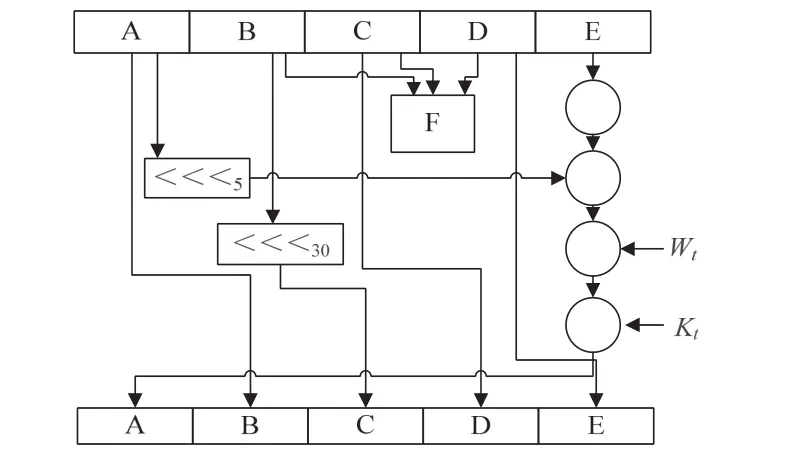
图1 SHA-1单个循环

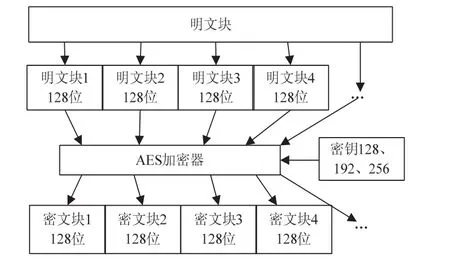
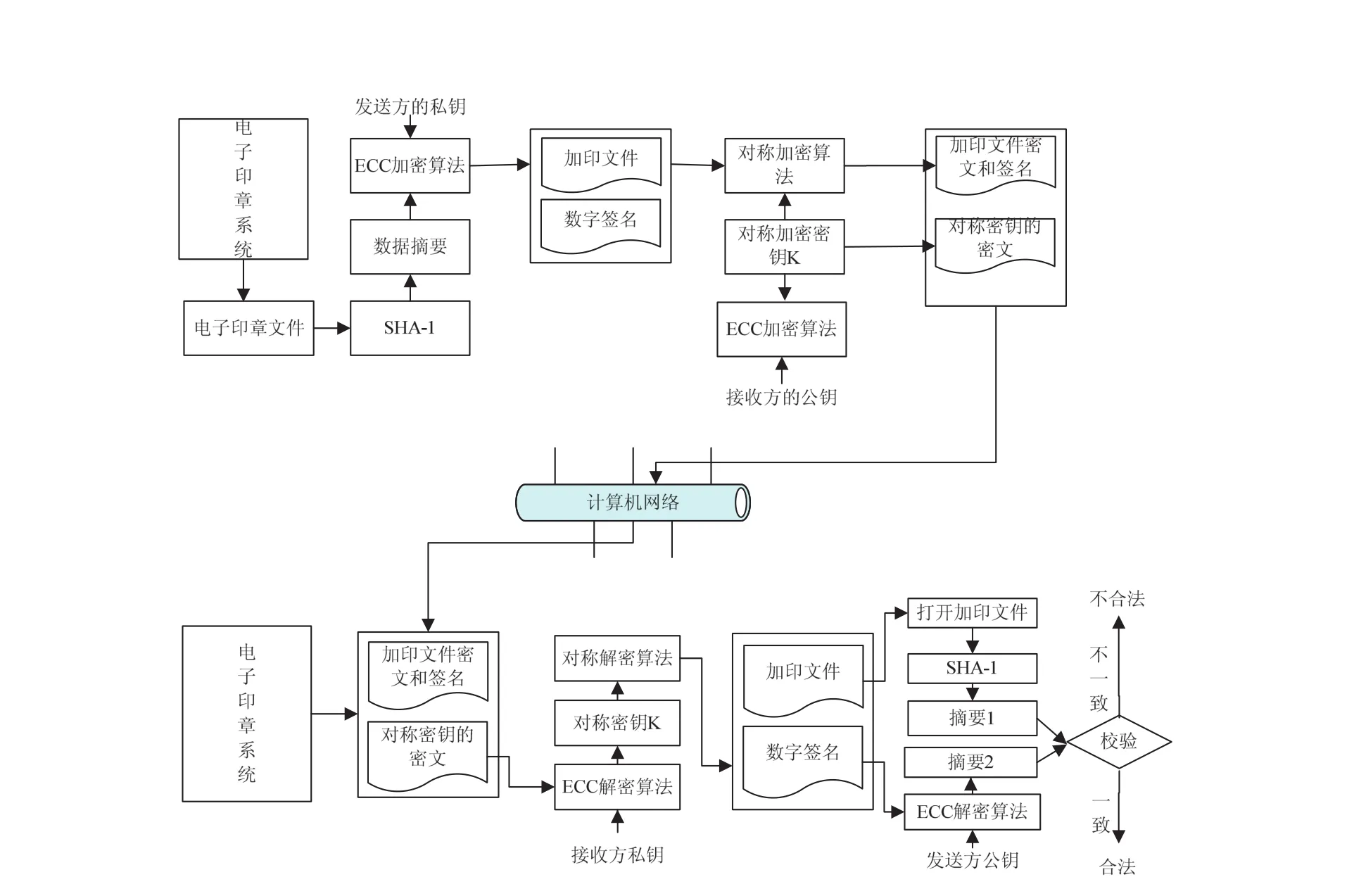
其中A，B，C，D，E 是这个状态中的32 位元文字，F是会变化的非线性函数，<<

1.3 高级加密函数

AES加密算法是密码学中的高级加密标准，是美国联邦政府所采用的区块加密标准，又称之为Rijndael加密算法[5]。该算法是由比利时的密码学家joan Daemen/和Vincent Rijmen所设计的，命名时结合了两人的名字，以Rijndael命名，由美国ANSI(美国国家标准学会)1997年发起征集，经过几轮的筛选，最终美国国家标准与技术研究院宣布了Rijndael算法作为新的AES算法。AES密钥长度分别支持128、192、256位，替代更早的DES加密算法，现已被分析证明是安全的，同时得到了世界的广泛使用。AES算法高级加密算法标准如图2所示。

图2 高级加密标准

2 ECC和SHA-1加印文件校验模型

加印文件校验是电子印章系统校验功能的一部分，校验加印文件的合法性。加印文件合法性是指按照电子印章系统的合法流程对电子文档加盖电子印章，在发送给接收方的过程中，不被非法查阅，接收方接收到加印文件后，加印文件符合通信双方事先的约定，文件具有完整性、真实性。

加印文件的合法性校验是指加印文件由发送方发送至接收方后，如果加印文件被伪造、破坏、篡改、传输错误，那么接收方应能够通过有效的方法检验出来，这种有效的检验方法就是加印文件的合法性校验。

所以依据据加印文件的合法性校验的定义，文中结合了ECC和SHA-1等相关技术，给出了加印文件合法性校验模型，如图3所示。

1)通过电子印章系统，生成所需的加印文件。

2)用SHA-1函数对加印文件进行运算，得到加印文件的摘要。

3)根据ECC签名原理，用发送方的私钥对加印文件的摘要进行签名。

4)用对称加密算法加密加印文件和数字签名，接收方公钥加密对称密钥，所有密文发送给接收方。

5)接收方收到加印文件及数字签名的密文后，首先用自己的私钥解密出对称密钥，用对称密钥解密密文，用发送方公钥验证签名，得到摘要2，用SHA-1得到摘要1，比较摘要1和摘要2是否相同，若相同，则加印文件合法，否则视为不合法。

图3 校验模型

3 模型实现

实现模型中的核心加密算法，实现加印文件具有身份认证、防伪造、防篡改、保密性、完整性、不可否认性。开发环境是在Windows平台下，使用JAVA语言，My eclipse平台作为开发工具[6]。

3.1 测试结果

本节主要给出加印文件合法性校验模型实现测试结果，对于测试部分，为了更好的显示测试效果，将加印文件以明文显示，以word文档测试以为例。如图4(a)为加印文件，图4(b)为测试结果。

图4 加印文件及测试结果

将图4(a)所示的加印文件，由发送方发送到接收方进行验证，加印文件的内容不做任何修改，其校验结果如图4(b)所示。

将图4(a)所示的加印文件，文件内容做出一些修改，将第一句中的“九”改为“八”，将修改后的加印文件发送给接收方。修改后加印文件的内容如图5(a)所示，将修改后的加印文件如图5(a)所示，同样进行测试，校验结果如图5(b)所示。

图5 加印文件及测试结果

4 结语

提出的校验模型，采用安全性更高的ECC和SHA-1替代安全性相对差的RSA[7]和MD5，同时结合了AES，改进了传统模型中加印文件被非法阅读的隐患，最终实现了加印文件的合法性校验，但是采用SHA-1对于大文件的效率，需要改进。

[1]宋泽芳.基于数字印章的文档签名问题的解决方案[J].哈尔滨工业大学学报,2005(07):835-837.

[2]范志强,李成,马兆丰,等.基于CPK组合公钥的电子签章技术研究[J].信息安全与通信保密,2011(07):98-102.

[3]张秀爱.椭圆曲线密码体制的研究[J].通信技术,2009,42(05):208-209,212.

[4]WANG X Y,YIN L S,YI Q,et al.Finding Collisions in the Full SHA-1[C]//Crypto 2005,LNCS 3621.Berlin:Springer-Verlag,2005:17-36.

[5]徐艳平,周玉洁.高级加密标准AES的高速实现[J].信息安全与通信保密,2006(04):81-83.

[6]刘淳,张凤元,张其善.基于智能卡的RSA与ECC算法的比较与实现[J].计算机工程与应用,2007,43(04):96-98.

[7]赵新,刘嘉勇.基于证书的RSA签名系统的设计与实现[J].通信技术,2011,44(02):73-74.