稳定匹配问题中的纳什均衡

王 烨，李雨生

（同济大学 数学系，上海 200092）

1 稳定婚配问题和纳什均衡

1.1 婚配问题

婚配问题最早是由Gale等［1］于1962年提出，这个问题和图论有关（求完全二部图的稳定完备匹配，这是一个NP问题）.

婚配问题是组合数学的一个重要问题，在一些关于组合数学的书籍中都有介绍［2-3］.婚配问题是要为n名男子与n名女子安排融洽的婚配关系.如果每名男子恰好适合与n名女子中的任意一个婚配，且每名女子恰好适合与n名男子中的任意一个婚配，则必定存在一个完美婚配.现在假设每个男子都有一个由与他合适婚配女子构成的集合，该集合中的元素是按照该男子对与他合适婚配女子的喜爱程度进行的有序排列，此排列称为该男子的喜好列表；同时每个女子也都有一个由与她合适婚配男子构成的集合，该集合的元素也是按照该女子对与她合适婚配男子的喜爱程度进行的有序排列，此排列称为该女子的喜好列表.

1.2 稳定匹配

假设二部图G＝G（n，n），V1＝｛a，b，…｝是男子的集合，V2＝｛A，B，…｝是女子的集合，其中｜V1｜＝｜V2｜＝n.在已知每个人喜好列表的前提下，定义二部图G的稳定匹配是一个独立边集合M，若aB∈E（G）-M，则存在W∈V2，使得aW∈M（a喜欢W胜于喜欢B），或存在m∈V1，使得mB∈M（B喜欢m胜于喜欢a）.

因此，由定义可知，若a没有和B结婚，则a与一个喜爱程度胜于B的人结婚，或B与一个喜爱程度胜于a的人结婚，否则a最终会和B结婚.

由上述分析可知，稳定匹配的结果不是唯一的，且不一定是完全匹配.但它是一个极大匹配，即此匹配不能再通过添加边使其变大.假设M∪｛aB｝是G中的一个匹配，且aB∈E（G）-M，若a，B都是独身主义者，则他们不会与心仪的对象结婚，在这种情况下，稳定匹配M是极大匹配，却非完全匹配.本文假设婚配中不存在独身主义者，所得的稳定匹配是一个完全匹配.

假设二部图G＝G（n，n），V1是男子的集合，V2是女子的集合，其中｜V1｜＝｜V2｜＝n，μ是图G 的一组匹配.匹配μ的中断对mW（其中m∈V1，W∈V2），是指mW∉μ，且m和W 都是喜欢对方胜于喜欢在μ中匹配的对象.因此，二部图G的匹配M 是稳定匹配，当且仅当M不存在中断对.

1.3 GS算法及复杂度分析

Gale等提出了稳定婚配问题后，也提出了著名的GS算法［1］（也称延迟认可算法），此算法可寻求到一组稳定匹配.

算法1（GS算法）

已知所有人的喜好列表，且不存在独身主义者.在第一轮选择过程中，让这些男子去向他们最心仪（喜好列表中排序第一）的女子求婚.等所有男子求婚完毕后，所有收到求婚的女子都从自己的求婚者中（根据个人的喜好列表）选择自己最喜欢的人并且接受他为未婚夫，没人求婚的女子只能暂时等一等.以上过程称为一轮，之后的每一轮都按照类似的方式进行.

在第一轮结束后，还处于单身状态的男子中的每个人再次向还没有对其求婚过的女子中自己最喜欢的人求婚（无论女子是否已经有了未婚夫），然后，等所有单身男子求婚完毕后，所有收到求婚的女子都从自己的求婚对象中选择自己最喜欢的人接受为未婚夫.原来有未婚夫而求婚者中有自己更喜欢对象的女子会换掉自己的未婚夫.等到这一轮完毕之后，再开始如上所述的新一轮的求婚.依此类推，当所有女子（男子）都已订婚时，算法结束.

为了计算GS算法的复杂度，在每一轮，接到求婚的女子有三种可能的情形，第一种是接受求婚者，第二种是拒绝这一轮的求婚者，第三种是解除婚约并接受这一轮的一个求婚者.对于第一种情形，她正好做一次选择，而对于后两种情形，她最多做（n-1）次选择，因此，对每名女子这种算法有O （n）步骤，因此总共有O n（2）步骤.

1.4 纳什均衡

Nash在1951年提出了纳什均衡的概念［4］.纳什均衡是参与博弈的每一个局中人在给定其他局中人策略的条件下选择上策（即：不管其他局中人采取什么策略，每个局中人都选择对自己最有利的策略）所构成的一种策略组合.

纳什均衡理论奠定了现代主流博弈理论和经济理论的根本基础，对经济和其他相关学科有着深远影响.

2 稳定匹配中的纳什均衡

本节研究纳什均衡与稳定匹配的内在联系.

命题1 稳定匹配是纳什均衡.

证明：假设图G的稳定匹配为M，则M不存在中断对.由稳定匹配的定义可知，若a没有和B结婚，则a与一个喜爱程度胜于B的人结婚，或B与一个喜爱程度胜于a的人结婚，否则a最终会和B结婚，即：对于∀aB∈M，a，B不能同时存在更优的匹配对象.而纳什均衡是指参与博弈的每一个局中人在给定其他局中人策略的条件下选择对自己最有利的策略所构成的一种策略组合，即：在给定别人策略的情况下，没有人有足够理由打破这种均衡.在稳定匹配M中，情况也是如此，任何一组匹配对中的点都不存在更优的匹配对象，因而没有足够的理由打破这种匹配，这正是纳什均衡的思想.

此外，如果对方的策略是确定已知的，那么自己的策略是最优的，而如果对方的策略是不确定未知的，那么自己的策略就很难是最优的.这与稳定匹配的思想一致，在GS算法中可以更为直观地理解这个问题，如果同一部集里其他人的选择是确定的（已知其他人的喜好列表），那么自己会有一个最优的选择，但如果其他人的选择是不确定的（其他人的喜好列表未知），那么自己的喜好列表顺序对自己的选择结果有着很大的影响，因而自己的选择很难达到最优.

3 GS算法编程

3.1 GS算法流程图

在Gale等提出GS算法后，一些人对GS算法进行了研究和改进［5-6］，其中Gusfield等针对稳定婚配问题的结构和算法进行了较为详细的研究［7］.而目前GS算法编程普遍采用的C语言，以输入参与婚配者的喜好列表方式进行编程运算.本文引入置换矩阵的表示方式，采用Matlab进行编程，表示形式更为直观.

对GS算法做一些改进.在GS算法中，Gale等规定每一轮中，还处于单身状态的男子中的每个人向还没有对其求婚过的女子中自己最喜欢的人求婚，等所有单身男子求婚完毕后，所有收到求婚的女子都从自己的求婚对象中选择自己最喜欢的人接受为未婚夫.现在，规定在每一轮中，还处于单身状态的男子中的每个人向还没有对其求婚过的女子中自己最喜欢的人求婚，不必等到所有男子求婚完毕后，女子就可以依次对男子向自己的求婚做出决定（接受或者拒绝），具体的GS算法流程见图1.这种每轮女子依次对男子的求婚做出决定的算法所得到的结果仍是一组稳定匹配.

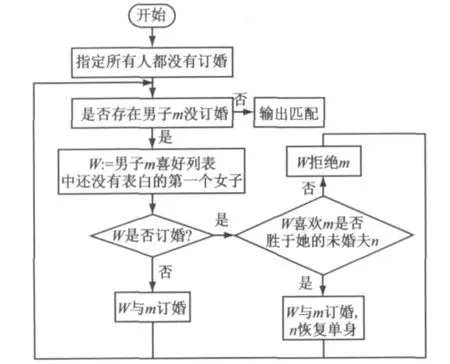
图1 GS算法流程图Fig.1 The flow chart of GS algorithm

3.2 GS的矩阵算法

假设二部图G＝G（n，n），V1＝｛a，b，…｝是男子的集合，V2＝｛a′，b′，…｝是女子的集合，且｜V1｜＝｜V2｜＝n.将男子a，b，…分别标号记为男子1，2，…，n；将女子分别标号记为女子1，2，…，n.设矩阵An×n中元素aij表示男子i的喜好列表中女子j的排列名次.矩阵Bn×n中元素bij表示女子i的喜好列表中男子j的排列名次，其中1≤i≤n，1≤j≤n.根据图1的GS算法流程图，做出了GS迭代算法，其中输出矩阵Cn×n是（0，1）矩阵，它表示一组稳定匹配，其中cij＝1表示男子i与女子j配对，cij＝0表示男子i与女子j没有配对.由于在稳定婚配中每名男子与一名女子结婚，同样每名女子与一名男子结婚，因而矩阵C不仅是（0，1）矩阵，而且还是每行每列恰有一个1的（0，1）矩阵，即矩阵C是置换矩阵.矩阵D1×n中元素di＝ni＋1，其中ni表示男子i已求婚的次数.

下面给出GS的矩阵算法：

参数：初始矩阵C＝0n×n（零阵），D＝I1×n（全1向量），矩阵An×n和Bn×n.

目标：输出矩阵Cn×n.

步骤1 输入初始矩阵C＝0n×n，D＝I1×n，以及矩阵An×n和Bn×n.

步骤2 若Cn×n的行列式为零，则寻找Cn×n矩阵的第i行为零，指派男子i向喜好列表中第di个女子求婚，该女子为j，即aij＝di.指定Cn×n矩阵中cij＝1.与此同时，di＝di＋1.若Cn×n的行列式不为零，转至步骤5.

步骤3 若Cn×n中存在第k列的计数（即第k列上所有元素之和）大于1，则搜索第k列中不为零的元素所处的行为k1，k2，…，取Bn×n中bk，k1，bk，k2，…的最小值的元素bk，ki.令cki，k＝1，Cn×n第k 列的其他元素为零.若Cn×n中每列的计数小于等于1，转至步骤4.

步骤4 若Cn×n的行列式为零，转至步骤2；若Cn×n的行列式不为零，转至步骤5.

步骤5 输出置换矩阵Cn×n.

4 算例

下面来具体解决一个婚配问题.考虑男子a，b，c和女子a′，b′，c′进行婚配，表1和表2分别是男子和女子的喜好列表，试图求解一组稳定婚姻匹配.

表1 男子的喜好列表Tab.1 The preference list of men

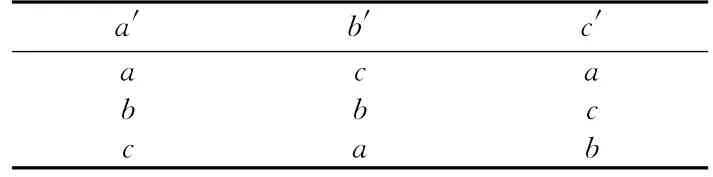
表2 女子的喜好列表Tab.2 The preference list of women

根据表1和表2以及上述A，B矩阵的定义，可知

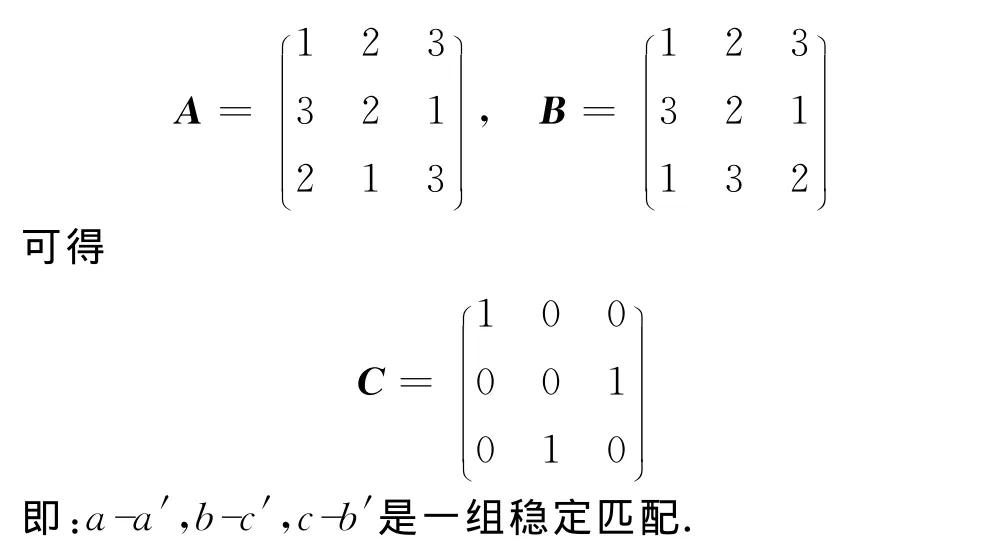
与传统的GS算法迭代运算相比较，此编程算法简洁明了，调用方便快捷.用矩阵的方法定义喜好列表，进而输出置换矩阵来表示稳定匹配，使繁琐的喜好列表顺序简单化，而且输入A，B矩阵之后即可调用函数，方法简单.但与传统的C语言程序相比，因为循环次数较多，Matlab程序运行时间会较长.此外，Matlab程序的运行结果只是其中一组的稳定匹配，并不是所有的稳定匹配输出结果，因而此编程还可以继续扩展.

5 图论中的纳什均衡思想

在图论中，除了稳定匹配问题外，很多问题也都蕴含着纳什均衡思想，这些思想对图论问题的理解和求解都有着很大的帮助.

（1）着色问题.最优着色问题是寻求一个k色图的真k着色.一旦此k着色确定，改变其中一条边的着色，此图的色数不会减少，因而没有达到优化的效果，即改变任意一边的颜色都不会使其优化，此图的着色也就趋向于均衡.

（2）最短路径问题.最短路径问题是图论研究中的一个经典算法问题，旨在寻找图（由节点和路径组成）中两节点之间的最短路径.每一条边都有两种选择，走此条边和不走此条边.最短路径一旦确定，其中任意一条边改变自己的选择，都不能使自己收益，路径也不会优化，因而最短路径的选择也趋向于均衡.

纳什均衡存在于生活中的每一个细微之处，在图论的很多方面都可以运用纳什均衡理论加以解释，对于解决图论问题也有着非常大的益处.

［1］Gale D，Shapley L S.College admissions and the stability of marriage［J］.The American Mathematical Monthly，1962，69（1）：9.

［2］Bollobas B.Modern graph theory［M］.New York：Springer，2003.

［3］Brualdi R A.Introductory combinatorics［M］.Upper Saddle River：Prentice Hall，2004.

［4］Nash J.Non-cooperative games［J］.Annals of Mathematics，1951，54：286.

［5］Dubins L E，Freedman D A.Machiavelli and the Gale-Shapley algorithm［J］.The American Mathematical Monthly，1981，88（7）：485.

［6］Huang C C.Cheating by men in the Gale-Shapley stable matching algorithm［J］.Lecture Notes in Computer Science，2006，4168：418.

［7］Gusfield D，Irving R W.The stable marriage problem：structure and algorithm［M］.Boston：MIT Press，1989.