亚临界雷诺数下圆柱体尾流结构的数值模拟

周 强，曹曙阳，周志勇

（同济大学 土木工程防灾国家重点试验室，上海 200092）

过去几十年来，圆柱体绕流问题因其简单的几何性质和丰富的流场特性，一直是空气动力学及风工程领域中的研究热点，尤其是对尾流结构的研究.在亚临界雷诺数范围内，桥梁中的吊杆、主缆以及拉索等具有圆柱形状的构件，在风的作用下产生规则的旋涡脱落和复杂的尾流结构，并发生风致振动而导致结构损伤或疲劳破坏.因此，研究在亚临界雷诺数下的圆柱体绕流问题及其尾流结构对工程结构设计有着十分重要的意义.

当雷诺数Re在40～2×105范围内，处于亚临界区的圆柱体绕流有着丰富的特性.已有文献表明当Re≈300～3000时，剪切层开始从圆柱体表面分离，并在尾流区呈现非定常的特性.同时在Re＝3900的情况下，Ong等［1］采用热线风速仪（hot-wire anemometry，HWA）方法测量了回转区外（3＜x／D＜10，D为圆柱体直径）的速度及涡量分布，Lourenco等［2］采用粒子成像测速（particle image velocimetry，PIV）技术测试了非常近尾流区（x／D≤3）流场结构，所以此后有关圆柱绕流的数值模拟及试验研究大多在这典型雷诺数（Re＝3900）下进行.Beaudan等［3］采用O形贴面网格和高阶迎风格式，并运用大涡模拟（LES）方法，对不可压缩的N-S方程进行求解，从而首先实现对此雷诺数下圆柱体绕流问题的数值模拟，其结果与Lourenco等［2］的试验结果很接近，但在回转区域内的平均流向速度分布形式表现以及回转长度Lr上均存在一些差别.Mittal等［4］同样运用LES方法，同时采用二阶有限中心差分格式及C形网格，结果显示在下游区的雷诺应力分布上与Lourenco等［2］的试验结果有一定的差别.Kravchenko等［5］采用基于B-splines的高阶方法进行数值研究，结果表明不足够的格子数将会导致回转长度减小，并且通过对比发现把展向长度从πD 增加到2πD 并不能影响结果，Breuer［6］得到同样的结果.此后 Franke等［7］、Parnaudeau等［8］也采用LES方法，Ma等［9］采用直接模拟（DNS）方法对圆柱尾流结构进行了研究.此外，Parnaudeau等［8］采用更先进的PIV设备对Re＝3900下的圆柱尾流结构进行了试验研究，结果与多个计算结果很近，而与Lourenco等［2］的试验结果有一些微小差别.国内学者周志勇［10］、李寿英等［11］都研究过此类问题，但均未给出详细的尾流结构.

本文采用二阶有限中心差分离散格式和O形贴面网格，并细化圆柱体周围5D范围内的网格，运用基于Smagorinsky亚格子模型［12］的LES方法，对均匀来流条件下的圆柱体绕流问题进行了三维数值模拟，验证了结果的准确性，并重点分析了尾流区的流场结构，从而得到一些有意义的结论.

1 控制方程与建模

1.1 控制方程

进行滤波后，LES的连续性和N-S方程为

式中：ρ为流体密度；ui，uj为速度分量；p为压力；μ为流体运动黏度；式中带有上划线的量为滤波后的场变量被定义为亚格子尺度应力，在Smagorinsky亚格子模型中

1.2 网格划分和算法

计算区域：30D×20D×2D.模型上游来流区域为10D，下游尾流区为20D，即x方向上的长度为30D；离上下边界各为10D，即y方向上的宽度为20D；展向长度为Lz＝2D，如图1所示.

网格划分：在圆柱周围5D范围，采用O型贴面网格，格子数为200×150；展向方向（z方向）的格子数设为60；在远离圆柱体的区域使用稀疏的网格，而在圆柱体附近尤其是在尾流区，采用密集网格；为保证计算的准确性，靠近圆柱表面的第一层网格的厚度取为d＝3×10-3D，然后网格以双曲切线表示的间距分布由内向外伸展；共1350000个单元.

图1 计算区域示意图及圆柱体周围网格划分情况Fig.1 Computational domain and grid example near the cylinder

边界条件：圆柱体表面边界条件采用无滑移固壁边界；来流边界条件采用均匀来流；出口边界采用压力出口，即压力梯度（内外压差）为零；在展向方向上（即z方向）的两个面，本文设置为周期性边界条件；上下侧面采用入流边界条件，设置速度为来流速度，法线方向上的速度为零.

2 数值验证

在数值模拟过程中，时间步长直接影响到数值结果的准确性.因此本文参考相关文献，设置时间步长Δt＝0.0025D／U＝6.4×10-4s.此外，在对数据结果进行统计处理时，所采用的数据数量将会影响到分析结果的准确性，因此需要考虑数据的统计时长.这里引入无量纲时间参数T＊＝nU／D作为统计时长（averaging time），其中n为实际流动时长，U为来流速度.因为n＝NcT，St＝fD／U，因此得到T＊＝Nc／St，其中T为旋涡脱落周期，f为旋涡脱落频率，Nc为旋涡脱落周期数.而对于Re＝3900的圆柱体绕流问题，其St数基本没有变化，因此统计时长T＊只和旋涡脱落周期数Nc有关.

如表1所示，Kravchenko等［5］采用7个旋涡脱落周期内的数据结果，即无量纲统计时长为T＊＝35.00.Dong 等［13］采用Nc＝40～50，即T＊≈200.00～250.00；Ma等［9］则采用 Nc＝131，T＊＝624.89；Franke等［7］认为在对数值结果处理时，需要采用40个旋涡脱落周期以上的数据，即T＊＞200.00；Parnaudeau等［8］分别统计了12个和52个旋涡脱落周期的数据，对比结果发现两者的结果均与试验结果很吻合；Beaudan等［3］仅统计了6个旋涡脱落周期的数据，同样取得较好的效果.因此本文在8个旋涡脱落周期（T＊＝38.00）内，对每个时间步的计算数据进行采样处理，以得到准确流场信息.

本文比较了St、平均阻力系数Cd、圆柱体后方平均压力系数Cpb、剪切层平均分离角θ、平均回转长度Lr等平均积分分量，如表1所示.图2比较了本文得到的圆柱体表面平均压力系数Cp、Kravchenko等［5］（Re＝3900）用 大 涡 模 拟 得 到 的 结 果 和Norberg［14］（Re＝4020）的试验结果.对比表明三者结果基本吻合，因此本文进行的数值模拟是有效和可靠的.

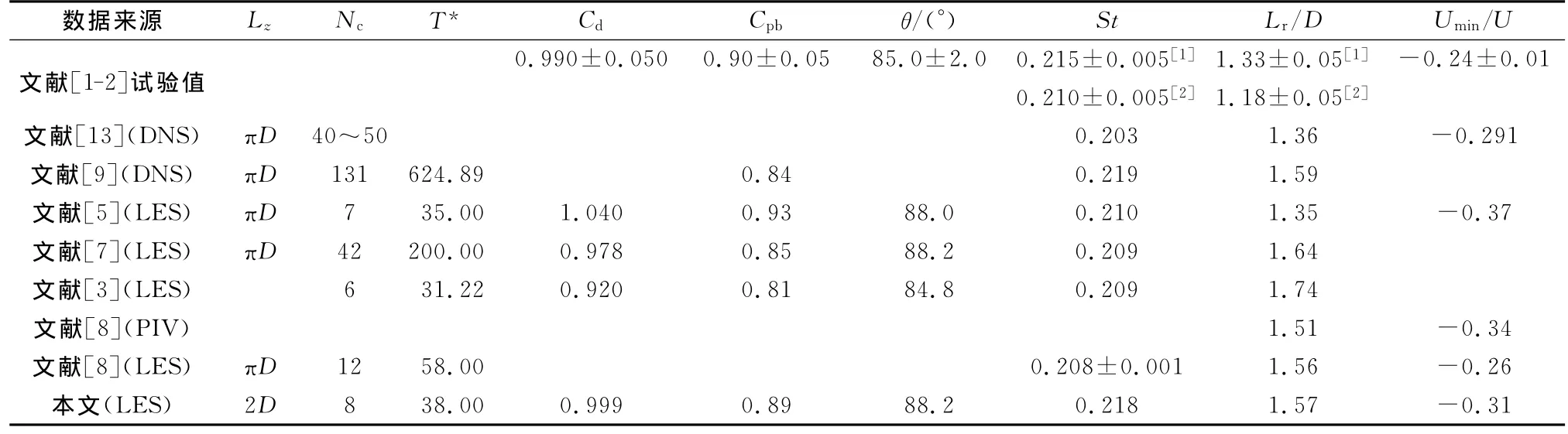
表1 平均积分分量对比表Tab.1 Comparison of the mean integral quantities

图2 圆柱体表面压力系数分布Fig.2 Pressure coefficient distribution on the cylinder surface

3 结果及讨论

3.1 平均积分分量

如表1所示，本文给出并比较了本文及其他文献中基于时间积分的平均积分分量，包括Cd，Cpb，θ，St，Lr（在这里引入回转长度，其定义为圆柱体中心到Umin对应位置的距离）以及最小来流速度与来流速度的比值Umin／U.对比本文结果与其他试验和数值结果，可以发现尽管Cd，Cpb以及Lr存在微小偏差，但还是可以认为其结果基本一致.同时还可以发现一个规律：当Lr越小时，其Cd，Cpb以及Umin／U 表现得越大.本文认为产生这个规律的原因是：Lr体现了在圆柱体后方形成的初始旋涡到圆柱体表面的距离，从而影响了圆柱体后方及其表面的负压强度，进而Lr的长短决定了Cd以及Cpb的大小，因此可以认为平均Lr起到指标性的作用.

3.2 平均流场特征

图3 中心线上平均流向速度分布Fig.3 Mean streamwise velocity distribution on the central line

图4 非常近尾流区不同位置上平均流向速度分布Fig.4 Mean streamwise velocity distribution at three locations in the very near wake

此外，在x／D＝2.02处平均流向速度分布上，本文结果和Parnaudeau等［8］结果吻合得很好，但较其他结果偏大.这是由于Lr的不同导致的.由图3可以看出 Kravchenko等［5］以及 Lourenco等［2］的Lr值更小，从而更早跳出回转区，因此在x／D＝2.02处u-的负值更小，甚至变正.由此可见，Lr是体现尾流流场结构的重要指标.

如图5所示，多个数值结果以及Parnaudeau等［8］的PIV试验结果表明，平均竖向速度分布应该是关于y＝0轴呈现反对称性，而Lourenco等［2］的结果并未表现出相类似的现象.此外由于Lourenco等［2］的试验采用的长径比L／D＝21，并且前方来流长度较短.因此本文认为导致数值结果与早期试验间偏差的主要因素是：圆柱体前方来流长度、长径比以及早期试验设备的测量误差.

图5 非常近尾流区不同位置上平均竖向速度分布Fig.5 Mean cross-flow velocity distribution at three locations in the very near wake

图6给出了近尾流区三个不同位置处的平均流向速度分布.由图可见，Ong等［1］与 Kravchenko等［5］的结果均与本文一致.同时可以看出，较非常近尾流区，此区域的平均流场速度u-的分布剖面更平滑，表明此区域内的旋涡强度不如上游区域.

图6 近尾流区不同位置处平均流向速度分布Fig.6 Mean streamwise velocity distribution at three locations in the near wake

3.3 湍流特性

从图7可以看出流向速度的脉动（u′u′／U2）在中心平面上的分布情况，其值从圆柱体表面的零值开始，然后逐渐增大，并达到两个峰值，然后缓慢单调地减小.对比其他数值模拟和试验结果可以发现，本文的数值模拟结果和Parnaudeau等［8］的LES结果基本一致，并且均表现为后一个峰值比前一个峰值更大；但是和Parnaudeau等［8］的PIV结果以及Norberg［15］（Re＝5000）的试验结果有些偏差，其原因还是在于来流长度和长径比的影响.此外，由于剪切层转变出现位置不同，导致回转长度的不同，从而使得脉动值的峰值出现位置以及峰值大小均表现不同.对于这一差别，后文中还将进行进一步解释.

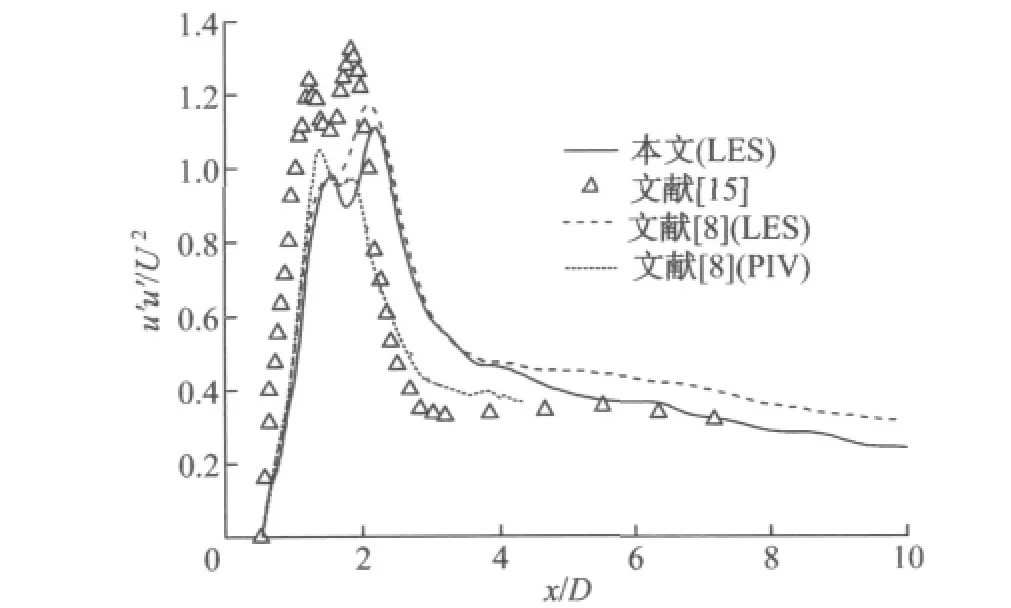
图7 中心线上流向速度脉动值分布Fig.7 Streamwise velocity fluctuation value distribution of the central line

由于旋涡的交替出现使得尾流区的流向速度脉动值在两侧出现峰值，而非在中心处，如图8所示.这表明尾流区出现卡门涡街现象.同时由图可见，在x／D＝1.06处出现尖角峰值，其原因在于x／D＝1.06处于回转区域内，即剪切层在这区域内发生转变，因此初始旋涡在这区域内交替出现，从而导致两端出现尖角峰值，随着流动向下游发展，峰值尖角消失，而变得更圆滑.此外由图可以发现多个结果基本吻合，而在x／D＝1.06和x／D＝1.54两处本文结果都稍小.如前面所述，出现这样差别的原因在于：剪切层转变出现位置不同，从而导致回转长度不同，进而使得脉动值的峰值出现位置也不同.如图8所示，当回转长度越小，其峰值越早出现，从而导致在回转区域内其对应的脉动值就越大，因此本文的脉动值在x／D＝1.06和x／D＝1.54较其他结果稍偏小.在尾流区其他位置上，本文结果与其他结果吻合得很好.

图9给出了非常近尾流区三个不同位置处竖向速度脉动值的分布.由图可见，在非常近尾流区竖向速度的脉动值均在中心线上达到峰值，并且可以发现数值结果比较一致，但与早期试验值有些偏差，其原因所前文所述.图10给出了近尾流区三个不同位置处的雷诺应力（u′v′／U2）分布，可见由于远离圆柱体，旋涡强度较小，因此在此区域内的雷诺应力值较小.

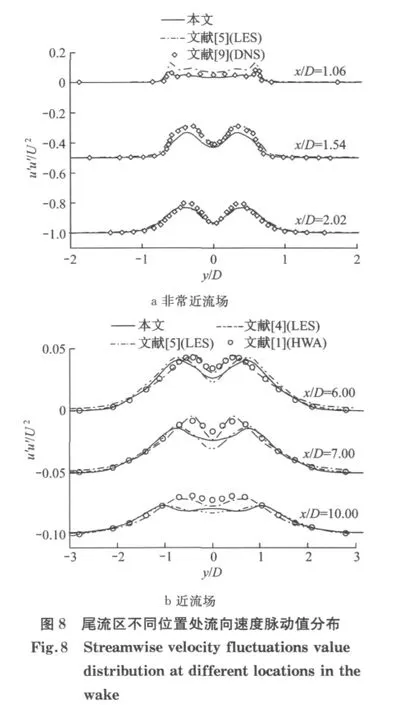
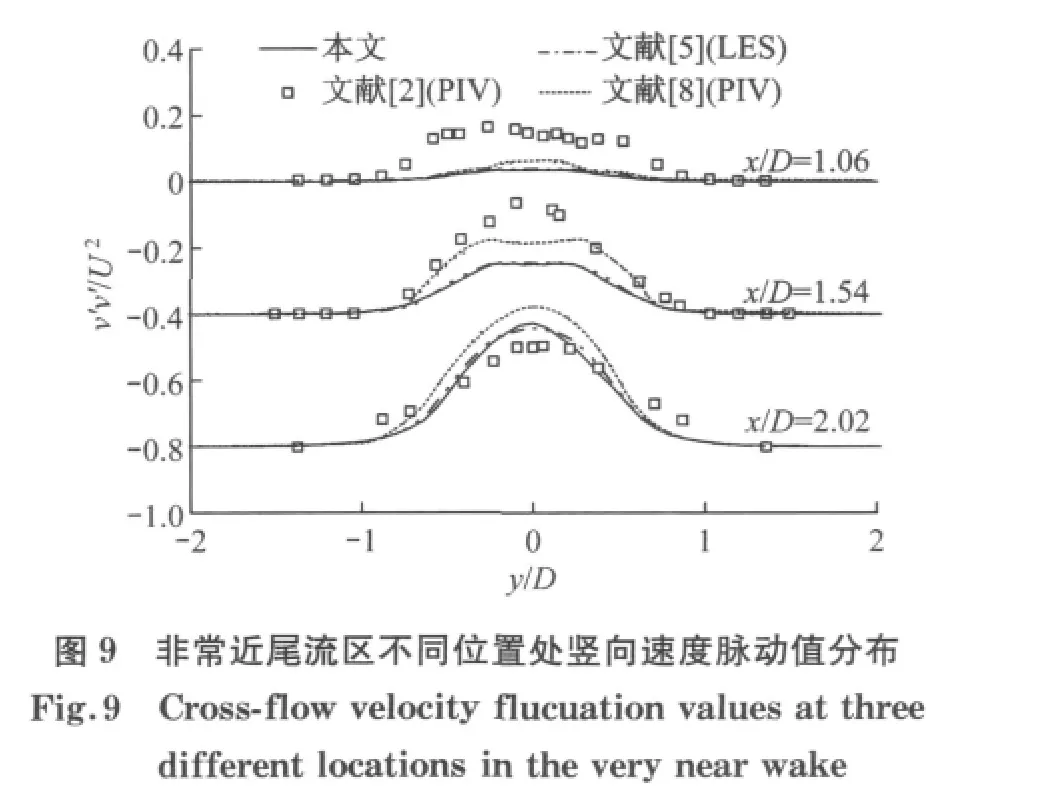
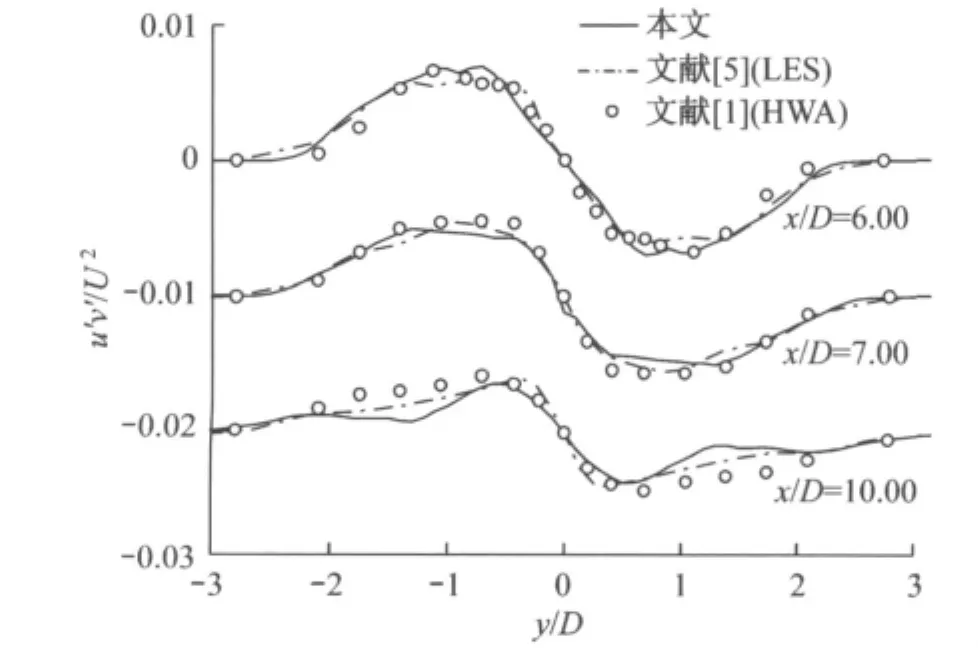
图10 近尾流区不同位置处的雷诺应力分布Fig.10 Reynolds shear stress distribution at three locations in the near wake

4 结论

（1）对St、剪切层平均分离角θ、平均阻力系数Cd以及圆柱体后方平均压力系数Cpb等平均积分分量进行比较分析，所得结果与试验值基本一致，从而验证了本文数值计算的准确性.

（2）详细给出了不同剖面处的平均速度、速度脉动值以及雷诺应力的分布，从而得到了尾流区的平均流场及湍流流场结构，为以后的试验和数值模拟提供详细的参考.

（3）通过分析与早期试验间存在的微小偏差，发现导致这种偏差的原因可能在于圆柱体前方来流长度、长径比的不同，并且需要进一步的试验和数值验证.

（4）回转长度是亚临界状态下圆柱体尾流结构中最重要的特征，是检验试验与数值计算的参考性指标.

［1］Ong L，Wallace J.The velocity field of the turbulent very near wake of a circular cylinder［J］.Experiments in Fluids，1996，20：441.

［2］Lourenco M，Shih C.Characteristics of the plane turbulent near wake of a circular cylinder.a particle image velocimetry study（data taken from ［3］），1993.

［3］Beaudan P，Moin P.Numerical experiments on the flow past a circular cylinder at sub-critical Reynolds number，TF-62［R］.Stanford：Department of Mechanical Engineering of Stanford University，1994.

［4］Mittal R，Moin P.Suitability of upwind-biased finite difference schemes for large-eddy simulation of turbulent flow ［J］.American Institute of Aeronautics and Astronautics Journal，1997，35（8）：1415.

［5］Kravchenko A G，Moin P.Numerical studies of flow over a circular cylinder at Re＝3900［J］.Physics of Fluids，2000，12（2）：403.

［6］Breuer M.Large eddy simulation of the sub-critical flow past a circular cylinder：numerical and modeling aspects ［J］.International Journal Numerical Methods Fluids，1998，28：1281.

［7］Franke J，Frank W.Large eddy simulation of the flow past a circular cylinder at Re＝3900［J］.Journal of Wind Engineering and Industrial Aerodynamics，2002，90：1191.

［8］Parnaudeau P，Carlier J，Heitz D，et al.Experimental and numerical studies of the flow over a circular cylinder at Reynolds number 3900［J］.Physics of Fluids，2008，20（8）：1.

［9］Ma X，Karamanos S，Karniadakis E.Dynamics and lowdimensionality of a turbulent wake ［J］.Journal Fluid Mechanics，2000，410：29.

［10］周志勇.离散涡方法用于桥梁截面气动弹性问题的数值计算［D］.上海：同济大学土木工程学院，2001.ZHOU Zhiyong.Numerical calculation of aeroelastic problems in bridges by discrete vortex method［D］.Shanghai：College of Civil Engineering of Tongji University，2001.

［11］李寿英，顾明.斜、直圆柱绕流的CFD模拟［J］.空气动力学学报，2005，23（2）：222.LI Shouying，GU Ming.Numerical simulation for flow around perpendicular and oblique circular cylinders ［J］. Acta Aerodynaimca Sinica，2005，23（2）：222.

［12］Lilly K.A proposed modification of the Germano subgrid-scale closure model［J］.Physics of Fluids，1992，4（4）：633.

［13］Dong S，Karniadakis E，Ekmekci A，et al.A combined direct numerical simulation particle image velocimetry study of the turbulent near wake［J］.Journal Fluid Mechanics，2006，569：185.

［14］Norberg C.LDV-measurements in the near wake of a circular cylinder［C］∥ Proceedings of the ASME Conference on Advances in the Understanding of Bluff Body Wakes and Vortex-Induced Vibration.Washington D C：ASME，1998：1-12.

［15］Norberg C.An experimental investigation of the flow around a circular cylinder：influence of aspect ratio［J］.Journal Fluid Mechanics，1994，258：287.