基于负梯度法的供水管网污染源识别

信昆仑，盛希夫，陶 涛，项宁银

（同济大学 环境科学与工程学院，上海 200092）

近几年，城市供水管网的突发污染事故屡有发生，除水源地污染引起管网饮用水问题之外，如管道错接等供水管网内部的原因也会造成水质的局部乃至全局恶化.因此，如何快速准确地定位污染源是饮用水安全保障急需解决的课题.关于污染源的定位研究，Laird等［1］提出了用非线性规划方法来求解这一问题.首先用源头追踪算法替代EPANET水质模拟计算引擎从而产生必要的数据，然后通过带正则项的非线性规划方法求出污染源侵入的时间和地点.针对这一方法解的非唯一性问题，Laird等［2］又提出了先用混合整数二次规划的方法确定一个候选污染源节点集，然后在此污染源节点集的基础上利用前一方法筛选出最有可能是污染源的节点.但这个方法对于大中型管网的适用性和此模型与实际管网相符程度仍然有待研究.Guan等［3］利用EPANET作为内嵌的水质模拟器再结合负梯度法提出了模拟优化算法.这一方法在已知管网模型的运行模式和水质监测数据充足可靠的前提下能够较好地解出污染源侵入的时间和地点.但只考虑了水质反应为线性的情况，也没有给出确定候选污染源节点的方法.Pries等［4］针对此问题提出了关系树-线性规划算法.通过构造上下游节点的污染物浓度关系树并形成线性规则，再利用关系树的线性规则反向求解线性规划问题，得到污染源节点位置及污染注入属性.Cristo等［5］提出了离散最优化的方法来求解污染源的识别问题.主要通过构造水质污染矩阵来确定可能的污染源注入点，再通过最小化模拟值和监测值的差来从可能的污染源点中确定污染源的位置.另外，Liu等［6］同样利用EPANET作为内嵌的水质模拟计算引擎用遗传算法随机搜索最优解.由于以上方法均需要管网的水质监测点可以报告实时的污染物浓度，对于水质监测点仅能判断是否出现污染物的情况，Yang等［7］提出用贝叶斯方法计算已检出污染物的水质监测节点其上游节点为污染源的概率，然后根据概率的大小判断出可能的污染源.

本质上来说，供水管网污染源的识别问题是管网水质模拟的反演问题，从数学的角度来看也是一个优化问题.本文基于Guan等［3］利用负梯度法求解供水管网污染源识别问题，结合Cristo等［5］提出的候选污染源节点集合方法，进一步考虑供水管网水质反应的复杂性，用差分步长法代替权重系数法求解梯度方向，采用EPANET作为内嵌的水质模拟计算引擎结合负梯度法来求解污染源侵入的时间、地点和侵入过程，并结合实例管网进行算法求解性能的分析.

1 模型构建

在城市供水管网拥有相当精度的水力水质模型且管网上安装了若各个水质监测点的情况下，污染源的识别问题可以转化为一个数学上的最优化问题.本文以模拟时段内各个水质监测点的实际污染物浓度值与模拟值差的平方和为目标函数，通过分析水质监测点不同时刻模拟浓度值与实测浓度值差来修正计算候选污染源在特定时刻的节点浓度.待模拟时段内所有的候选污染源节点浓度更新后，再次进行水质模拟.当模拟结果达到预设的条件后，输出候选污染源节点浓度矩阵.由于求解所得的候选污染源污染物累计注入量与其作为真实污染源的可能性成正比，因此可以此作为确定污染源节点的依据.

首先定义

式中：xi（t）表示候选污染源节点i在t时刻的污染物浓度值，对于k个时间段，则xi是一个行向量，即xi＝［xi（t1），xi（t2），…，xi（tk）］；yj（t）表示水质监测点j在t时刻的模拟污染物浓度值；n表示候选污染源节点总数；m表示布置的水质监测点总数；t表示模拟时刻.

监测点模拟浓度可以表示为

结合监测点的实际监测结果，污染源识别问题的目标函数可以表示为［3］

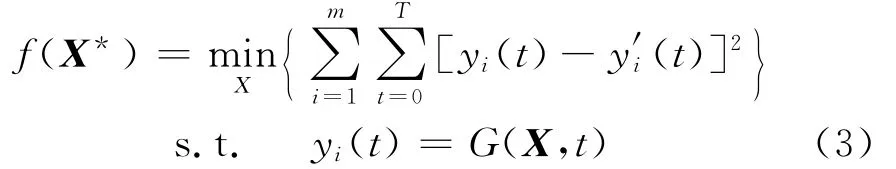
式中：X＊为污染源识别问题的最优解，y′i（t）为水质监测点i在t时刻的实际浓度值.为了便于求解，这里需作几点假设：①污染物的流量相对于管网水量而言可忽略不计，不影响管网原来的水力工况；②污染物在管网节点处投加，投加点可以是多个，投加量可以随时间变化，但在每一水质时间步长之内是恒定不变的；③污染物侵入管网中每个节点的概率是相同的，也就是说污染物是随机侵入的；④管网中的水质监测点能够监测到任意浓度的污染物.

2 模型求解

由于式（3）表示的最优化问题目标函数和约束条件均为非线性函数，且约束条件是由供水管网恒定流方程、连续性方程、管道水质反应动力学方程共同决定的复杂非线性等式约束，因此该问题为高度复杂的非线性规划问题.考虑到约束条件可采用成熟的EPANET水力水质分析模块进行隐式求解，故基于负梯度法，通过差分法求目标函数梯度向量对此非线性规划问题进行求解.求解过程如下：

步骤1 给定初始近似点X（0）及精度ε＞0，若‖▽f（X（0））‖2≤ε，则X（0）即为近似极小点.需要说明的是梯度向量的每一个元素均为目标函数对X＝［x1，x2，…，xn］相应元素的偏导数.该偏导数通过差分法近似求解

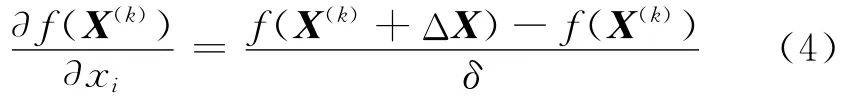
式中：ΔX是第i个元素为δ且其余元素为0的列向量；δ为差分步长，其取值大小应该合理确定；f即目标函数（见式（3））.当水质反应为线性关系时，水质监测点所测得的污染物浓度值可以表达成污染物侵入节点的污染物浓度加权值［3］，即

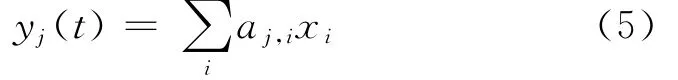
偏导数的求法可以简化为

式中：aj，i为水质监测点j对候选污染源节点i的权重系数，即当候选污染源节点i有一个单位的增量时，在水质监测点j有相应的污染物浓度增量.权重系数可以通过EPANET水质分析中的源头追踪功能得到.

步骤2 若‖▽f（X（0））‖2＞ε，求步长λ0，并计算

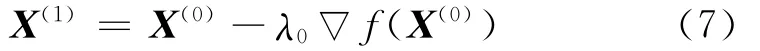
求最佳步长本文采用黄金分割法，最佳步长即为使得目标函数最小的步长.若‖▽f（X（1））‖2≤ε，则输出X（1），否则转入步骤3.

步骤3 一般地说，若‖▽f（X（k））‖2≤ε，则X（k）即为所求的近似解；若‖▽f（X（k））‖2＞ε，则求步长λk，并确定下一个近似点

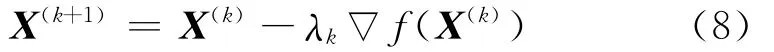
如此迭代下去，直至达到所设定精度要求为止.

3 算例研究

以供水管网实例Net3为例进行污染源的识别问题求解.Net3管网模型含节点数92个，水库2座，网中水塔3个，管段数117个，水泵2台，如图1所示.图中虚线范围内的节点为候选污染源节点.

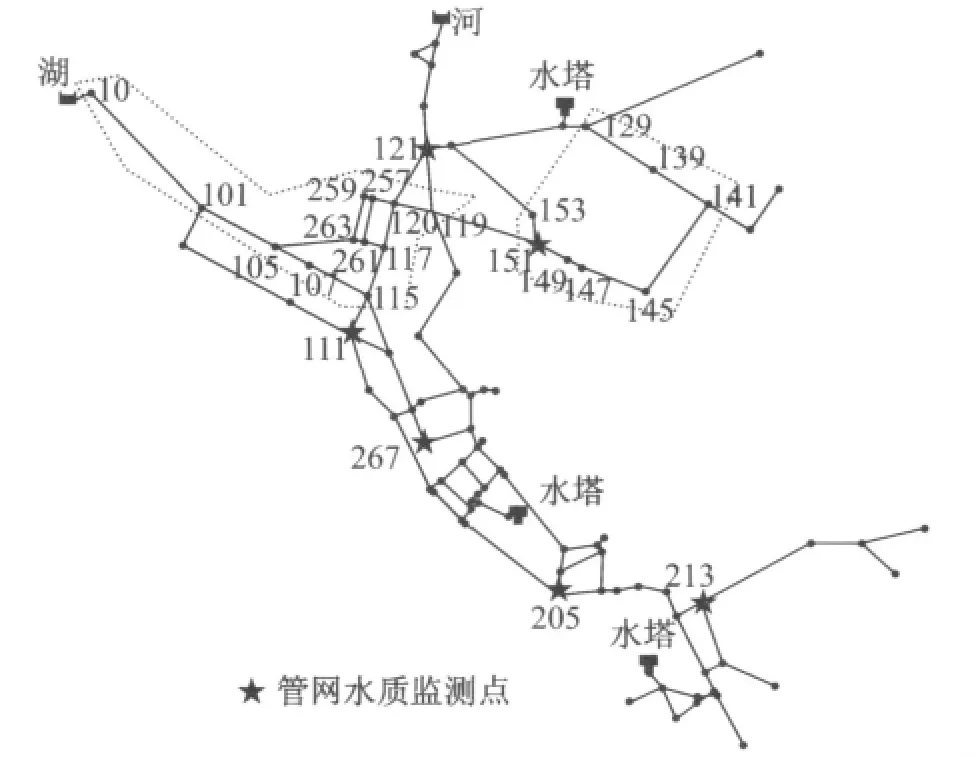
图1 管网拓扑结构图Fig.1 Topology layout of the case study network

假定在节点101和119同时注入污染物，注入方式为设置点注入［8］，注入时间段为3∶00am～10∶00am，污染物注入质量浓度变化模式见图2.管网水质模拟时间总长24h，水力时间步长1h，水质时间步长5min.在管网中随机选取6个节点作为水质监测点（分别为连接节点121，151，111，267，205，213），如图1所示.通过水质模拟，以这些节点模拟污染物质量浓度数据作为监测结果数据（见表1）.

表1 监测点模拟污染物质量浓度Tab.1 Simulated concentrations at monitoring sites mg·L-1

3.1 确定候选节点集

候选节点集是指根据水质监测点对污染物的监测情况所确定的可能是管网污染事故污染源发生位置的节点集合.目前关于管网突发污染事故污染源追踪的研究，仍然以通过经验法确定候选节点集合为主［3］，候选节点集合确定的范围和准确程度都会影响到污染源识别问题最优化算法的性能.为此，本研究根据文献［5，9］提出的最小覆盖集方法进行候选节点集合的确定.首先求出节点的监测时间矩阵，以24h为它们的服务水平，可以确定出每个监测点所覆盖的范围.通过表1可知，本次污染事故假定模式下，实际上仅水质监测点151，111，267，205，213能监测到污染物.因此可以把5个监测点共同覆盖的节点作为候选节点集（如图1所示），即

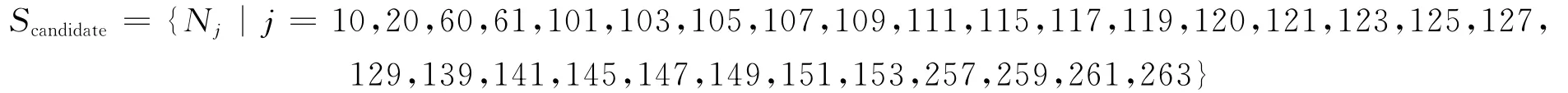
3.2 结果分析

考虑到按照负梯度方向搜索得到的是局部最优解，且绝大多数候选污染源节点均不是污染源注入点，可将初始解向量的每个元素均设置为0.求解过程中，差分步长δ取0.0100，最高迭代次数取360.图2中显示采用差分法计算梯度向量求解得到的结果，由于求解的多数候选点的质量浓度值均很小，图中仅显示30个候选污染源节点中所求解的注入质量浓度较大的4个节点的注入质量浓度随时间变化情况.候选污染源节点101是各时刻累计投加质量浓度值最大的节点，初步选定为污染源节点.同时，候选污染源节点10从3∶00am到10∶00am基本上以100mg·L-1的质量浓度持续注入.图1表明，节点10和节点101是同一个管段的起止节点.该现象表明有一个污染源在以节点10和节点101为起止节点的管道中.事实上，候选污染源节点101的注入质量浓度变化曲线基本与实际污染源节点101的质量浓度变化曲线相吻合.此外，候选污染源节点119的投加质量浓度呈抛物线型变化也与实际的污染源119投加质量浓度变化相吻合，可以确定这里也是一个污染源注入点.另外，候选污染源节点151作为污染源节点119的邻近节点，也有一定质量浓度的污染物注入，这就更表明了另一个污染源就是节点119或者在其附近.

图2 污染物注入质量浓度变化曲线（差分法）Fig.2 Injection concentrations of contamination source（finite difference method）

3.3 影响求解结果的因素分析

（1）差分步长

对于图1所显示的小型算例管网，将迭代次数均设定为360次，差分步长δ依次取值为0.1000，0.0100，0.0010和0.0001时，计算结果的梯度向量模长值依次为16.52，0.24，0.15和0.33.为了定量地衡量计算结果与实际结果的拟合程度，计算污染源节点101和119各个时段假定注入浓度和解出注入浓度差的平方和总和，依次为：1564.09，1914.74，7703.17，64201.58，如表2所示.

由表2可知，差分步长取0.0100时对应的计算结果（梯度向量模长为0.24，目标函数值为1914.74，而梯度向量模长和目标函数值是反映梯度法求解质量的两个主要指标）最好，此时差分步长取值正好与EPANET水质选项中设定的水质公差值相同.其原因在于水质公差表示管网水质的最小变化值，也即一部分水体与另一部分水体水质的最小差值［9］，这个值也表征了管网中水质监测点的污染物最低监测限度，因此当差分步长取水质公差值时，计算结果最好.若差分步长继续减小，由于梯度计算将逐步超出管网模型的计算精度范围，计算结果反而变差.

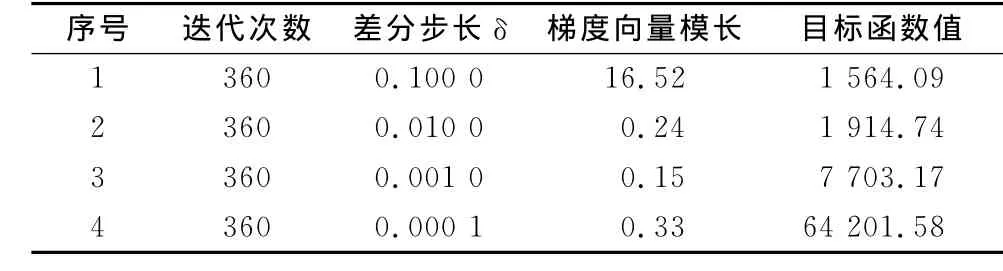
表2 差分步长求解结果对比Tab.2 Comparison of results with differentδs

（2）梯度计算方法

针对本文研究的算例管网，分别分析了通过差分法（见式4）以及线性比例法（见式6）进行梯度计算的求解效果.线性比例法计算后得到的结果如图3所示，其中迭代次数为400次，收敛时间为1min，梯度向量的模长为3230.83；通过差分法编码计算后得到的结果如图2所示，其中迭代次数为400次，收敛时间为5min，梯度向量的模长为0.25.

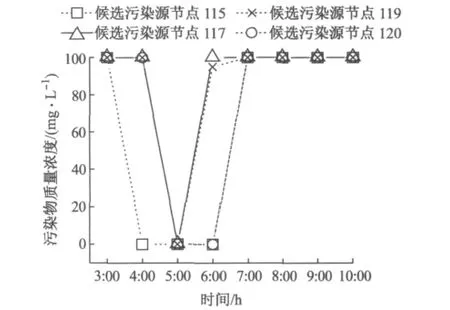
图3 污染物注入质量浓度变化曲线（线性比例法）Fig.3 Injection concentrations of contamination sources with linearly proportional method

图3表明在候选污染源节点115，117，119和120处有污染物注入，所定位出的污染源位置在假定污染源注入点附近区域，但对于污染源节点污染物浓度的变化识别精度较差；而通过差分法计算（见图2）则能够直接确定污染源注入的时间、地点和侵入过程.此外，迭代次数相同时，采用线性比例法计算结果的梯度向量模长远大于采用差分法计算的梯度向量模长.因而采用线性比例法计算的结果要比用差分步长编码计算的结果差，但用线性方式编码计算的收敛速度快于用差分法计算的速度.在采用线性比例法进行计算时，还需要为迭代变量设置一个可取值区间，以保证解的非负性和所能取的最大值，否则将会出现无法收敛的情况.而用差分法计算时，仅需要保证解的非负性，无需设置解的最大限值.分析其原因在于，线性比例法计算时，由于水质监测点对于某一候选污染源节点的权重系数，是取相应时间步长时段内的权重系数平均值，因此所求得的梯度向量并不能精确地给出目标函数的收敛方向，导致计算结果较差.因此，建议在需要快速确定污染源点位时可采用线性比例法，当需要更精确地分析污染物注入时间、浓度及变化模式时，采用基于管网水质模拟的差分法进行计算.

4 结论

负梯度法可有效解决供水管网单点污染物注入模式和多点污染物注入模式下的污染源定位问题.相对于遗传算法等随机搜索算法，沿负梯度方向搜索具有更高的搜索效率，通过引入差分算法可有效降低目标函数对于决策变量求导的难度.而通过将利用最小覆盖集确定候选污染源节点集合的方法与梯度法相结合，可进一步提高对污染源识别问题的求解能力.此外，通过不同差分步长下的计算结果表明，当其值取水质模拟所采用的水质公差值时，算法求解结果最好.而相对于用线性比例法求解梯度向量，差分法可获得更高的求解质量，不但可以定位污染源，并能以较高精度识别污染物注入的时间和浓度变化模式.

由于污染源识别问题是利用有限个水质监测点获得的数据反演污染源的侵入过程，因此，水质监测点的数量及空间布置对于问题的求解有直接的影响.因此，在将来的研究中，本方法应进一步与水质监测点的优化布置结合，以更进一步提高算法的求解效率.此外，对于无法有效获取管网中水质的精确浓度数据的情况，如何对突发污染事件进行污染源的辨识，是未来需要进一步研究的问题.

［1］Laird C D，Biegler L T，van Bloemen Waanders B G，et al.Contamination source determination for water networks［J］.Water Resources Planning and Management，2005，131（2）：125.

［2］Laird C D，Biegler L T，van Bloemen Waanders B G.Mixedinteger approach for obtaining unique solutions in source inversion of water networks［J］.Water Resources Planning and Management，2006，132（4）：242.

［3］GUAN Jiabao，Aral M M，Maslia M L，et al.Identification of contaminant sources in water distribution systems using simulation optimization method：case study ［J］. Water Resources Planning and Management，2006，132（4）：252.

［4］Pries A，Ostfeld A.Contamination source identification in water systems：a hybrid model trees-linear programming scheme［J］.Water Resources Planning and Management，2006，132（4）：263.

［5］Cristo D C，Leopardi A.Pollution source identification of accidental contamination in water distribution networks［J］.Water Resources Planning and Management，2008，134（2）：197.

［6］LIU Li，Ranji Ranjithan S，Mahinthakumar G.Contamination source identification in water distribution systems using an adaptive dynamic optimization procedure［J］.Water Resources Planning and Management，2011，137（2）：183.

［7］YANG Xueyao，Boccelli D L，De Sanctis A E.A Bayesian approach for probabilistic contaminantion source identification［C］／／World Environmental and Water Resource Congress.［S.l.］：ASCE，2011.

［8］Rossman L A.EPANET2 users’manual［M］.Cincinnati：U.S.Environmental Protection Agency，2000.

［9］王凤仙.供水管网水质管理软件应用和预警技术研究［D］.上海：同济大学环境科学与工程学院，2010.WANG Fengxian.Study on application of water quality management software and early-warning technology for water distribution systems［D］.Shanghai：College of Enviromental Science and Engineering of Tongji University，2010.