自升式平台风载荷的空气动力学干扰研究

林 一，胡安康，孙 建

（1. 哈尔滨工程大学，哈尔滨 150001；2. 中集船舶海洋工程设计研究院，上海 201206）

0 引 言

由于自升式平台进行钻井作业时处于抬升站立状态，随着风高度的增加导致风载荷增大，因此在设计阶段风载荷是最主要的控制载荷。目前对于自升式平台风载荷的计算方法均取自各大船级社规范[1]，主要采用面积投影法，忽略结构件空气动力学干扰的影响，这种处理方法将导致计算结果偏于保守，不利于结构的优化设计。参考文献[2]将北海一艘半潜式平台上实测的风力值和按挪威船级社（DNV）规范计算的风力值进行比较，记录的300多组数据均表明实测观察值仅为计算值的50%；参考文献[3]对一艘半潜式平台进行风洞实验后发现，实验结果小于按美国船级社（ABS）规范计算的值。哈尔滨工业大学[4,5]通过风洞实验和数值模拟对HYSY-981半潜式平台的风载荷与表面风压分布进行了研究，具有一定的参考价值。但是上述研究并未对造成这种结果差异的原因，即空气动力学干扰现象作进一步分析。

空气动力学干扰的研究重点主要集中在复杂高层建筑上，对于海洋平台研究甚少。自升式平台工作状态处于开阔海面，属于我国“建筑结构荷载规范”中的A类地貌，干扰效应最为显著[6]，因此应予重视空气动力学干扰现象。自升式平台甲板利用率很高，布置紧凑，导致上层建筑、桩腿、井架、悬臂梁等结构在受风时相互遮蔽，大大减小了整体的风载荷。由于结构较多，导致处理其风致干扰现象时与建筑群体类似，需要借助风洞实验或者数值模拟技术。

1 风洞实验

1.1 平台基本参数

本文选用的122m自升式钻井平台采用三桩腿桁架式结构，见图1。桩腿为菱形连接，最大工作水深122m，气隙12.2m，最大钻井深度9150m，入级ABS船级社，平台基本参数为：

主尺度（总长×型宽×型深）：70.40m×74.20m×9.40m；井架（高度×底部宽度×二层台宽度）：51.82m×12.19m×5.49m；桩腿长度：166.98m

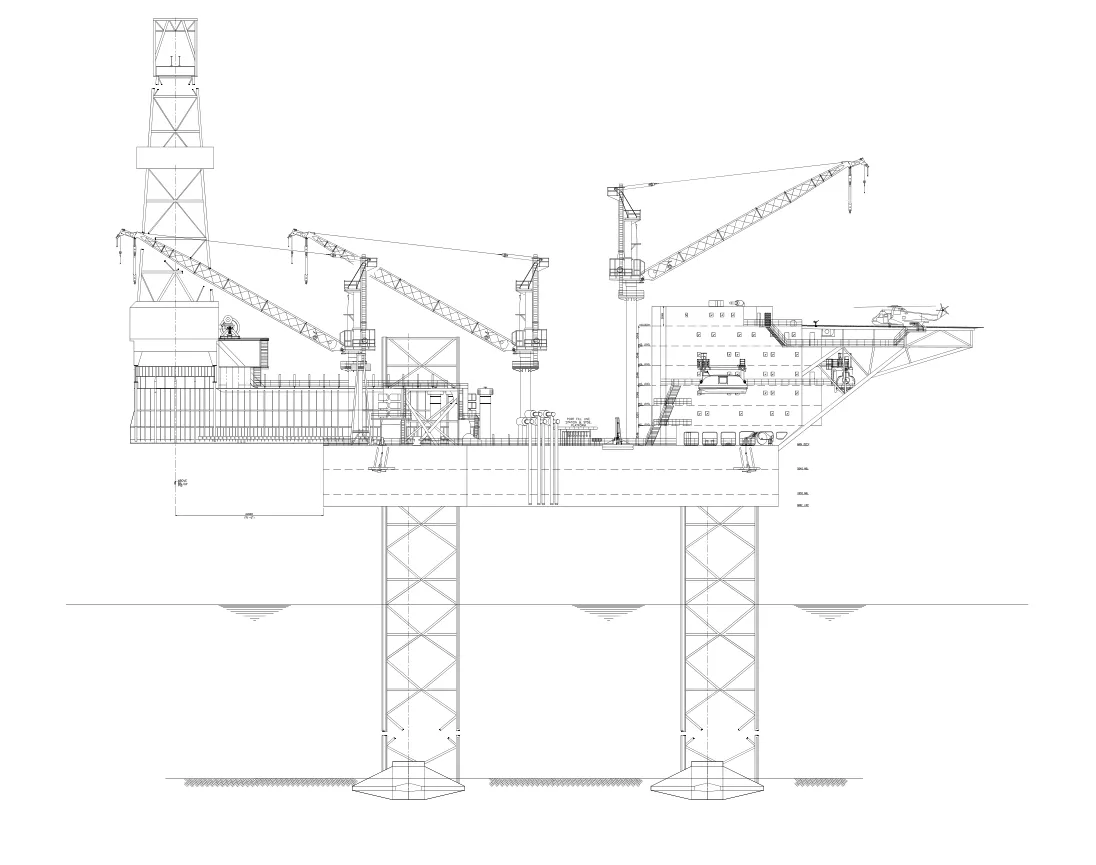
图1 平台

图2 坐标系统

1.2 实验条件及实验模型

风洞实验的目的是考察自升式平台的空气动力学干扰现象，即整体模型风载荷与各构件风载荷之和的比较。该实验委托国际知名的安邸建筑与环境工程国际咨询公司（RWDI）在英国Dunstable风洞实验室进行。该实验室拥有一座全钢结构回流式边界层风洞，试验段长16.3m，横断面宽2.4m，高2m，最大设计风速24m/s。

平台风洞试验模型是以122m自升式钻井平台为参考，按1:200缩尺制作的刚性模型。钻井平台被安装在五分力基底天平上，用于测试风载荷。在风洞实验之前，通过加载实验，对天平进行标定。风洞实验中采样频率为100Hz，模型采样长度为60s，相对于实际尺度45min。实验中，整体结构上力和力矩的坐标系统可参照图2，实验选取12个风向角，在0～360°范围内，以每30°风向角为角度间隔。

图3 正常工作状态

图4 风暴自存状态

整体实验模型见图3、4，各构件模型见图5、7。由于实验条件的限制，不可能将结构分得过细，因此将整个平台分为3个主要的受风结构：桩腿、井架、主船体+悬臂梁，这种处理方法已能反映出主要结构的相互干扰作用。

1.3 实验风速和风向

对于自升式平台的风载荷实验，最重要的是模拟大气平均风速剖面，即保证流动相似[7]。该实验中，通过在风洞工作段前方设置适当的紊流发生装置和地面粗糙元进行模拟，以获得所要求的风速剖面和紊流结构，实现流速沿高度变化，其中平均风剖面幂指数为0.09。

图5 主船体+悬臂架

图6 井架

图7 桩腿

2 数值模拟

2.1 控制方程

由于平台局部构件多为钝体，其控制方程采用雷诺时均 Navier-Stocks（RANS）方程，应用有限体积法离散控制方程；差分格式采用高阶中心格式；湍流度采用一阶模式，基于雷诺时均的控制方程可写为：

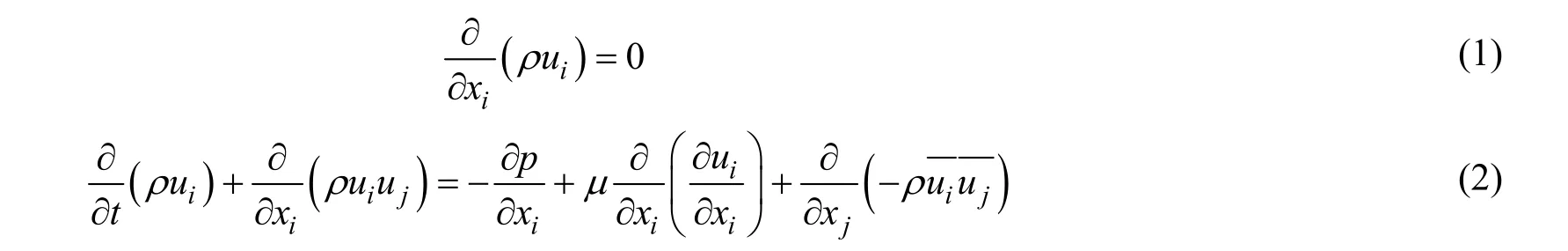
式中，i,j = 1,2,3；

ρ——空气密度，取1.225kg/m3；

4)定期检查SR与BRR调节器脉冲管路。燃烧系统是一种空气引导系统，空气流量增加或减小变化时，燃气流量也发生变化。SR与BRR调节器脉冲管路由燃气比率调节阀与混合器之间的均压环引出脉冲空气来调节燃气的通过量，若有任何泄漏，将导致调节器不连贯操作。因此，需用泡沫水定期检查接口处是否存在泄漏。

μ——动力黏性系数，取 1 .789 4× 1 0-5kg/(m⋅ s)。

2.2 湍流模型

湍流模型的选取对计算精度有着直接的关系，当前许多学者提出的各种湍流模型或多或少都带有一定的经验成分[8]，参考文献[9]认为计算精度的大体顺序是RSM，RNGkε-，SSTkε-，标准kε-，但对于湍流模型的适用性，业界也多有争议。本文以井架为计算模型，通过比较选择合适的湍流模型，计算结果（见表1）表明，湍流模型的选取对结果影响不大，约1%左右。这是由于桁架式结构受力主要来源于压差阻力，摩擦阻力所占比重较小，各湍流模型计算精度差别在于对边界层的模拟，边界层主要影响摩擦阻力，因此导致计算结果相差较小。基于此点考虑计算速度，在整体模型计算中湍流模型选取标准kε-模型。

表1 不同湍流模型计算结果

2.3 边界条件

入口边界采用速度入口，参照参考文献[1]，风速大小沿高度分布函数取为：

出口边界采用开放出口，流域顶部、底部和两侧采用无滑移壁面条件，结构壁面采用无滑移壁面条件，内域和外域通过交界面连接。

3 结果分析

3.1 整体风载荷比较

为了更好地反映空气动力学干扰，特别是遮蔽效应现象对自升式平台整体风载荷的影响，对规范计算、风洞实验和数值模拟结果进行了对比（见图 8、9）。基于目标平台入级 ABS船级社，主要依据 ABS的MODU规范进行风载荷的计算。规范规定对于无限作业区域的平台，其最小设计风速应为：（a）风暴自存工况：51.5m/s（100kn）；（b）正常作业工况：36m/s（70kn）。在计算风载荷时，风压按式（4）取值，风力按式（5）取值。

式中，kV——设计风速；

Ch——高度系数；

A——平台在正浮或倾斜状态时，受风构件的正投影面积。

图8 正常作业状态的风载荷

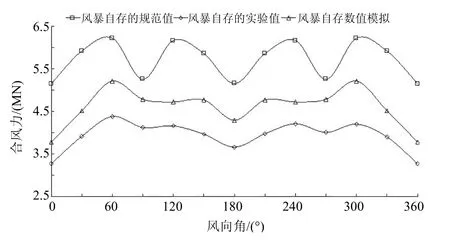
图9 风暴自存状态的风载荷

数值模拟计算的结果在趋势上与风洞实验结果更为类似，规范计算值的变化趋势明显有所偏差。由于遮蔽效应的影响，数值模拟和风洞实验的结果均小于规范计算值。其中，正常作业状态下，数值模拟的风载荷平均小于规范计算约18.95%，风洞实验平均小于规范计算约28.6%；风暴自存状态下，数值模拟的风载荷平均小于规范计算约19.36%，风洞实验平均小于规范计算约31.2%，说明随着风速的增大，规范计算的保守性显得更为明显。

从风向角来看，0°角左右的结果相差最大，90°和270°的结果相差相对较小。这是由于0°角时，平台的上层建筑对其下风向的桩腿、悬臂梁和井架存在较为明显的遮蔽效应；而90°和270°角时，遮蔽效应的影响减到最小。从结果对比可知，规范计算由于不计及各构件间遮蔽效应的影响，因此偏于保守，其随风向角变化的趋势也与实际情况有所偏差。数值模拟的结果位于两者之间，但在趋势上与风洞实验结果吻合良好，因此可以认为其计算结果准确可信，可以将其应用到工程设计中。

3.2 空气动力学干扰分析

为了更好地表征空气动力学干扰现象对于自升式平台风载荷的影响，特意引入建筑工程中风载荷的衡量指标：干扰因子IF[10]（见式6）。建筑工程中对于IF值多有研究，相应规范中甚至有供工程师参考的推荐值，如澳大利亚规范推荐干扰因子根据建筑之间的间隔参数取0.7～1.0。虽然建筑工程的风载荷结果不能直接引用到海洋工程风载荷计算中，但仍具有一定的参考价值。

式中：CF,inter——有干扰体情况的风载荷；CF,iso——无干扰体情况的风载荷。

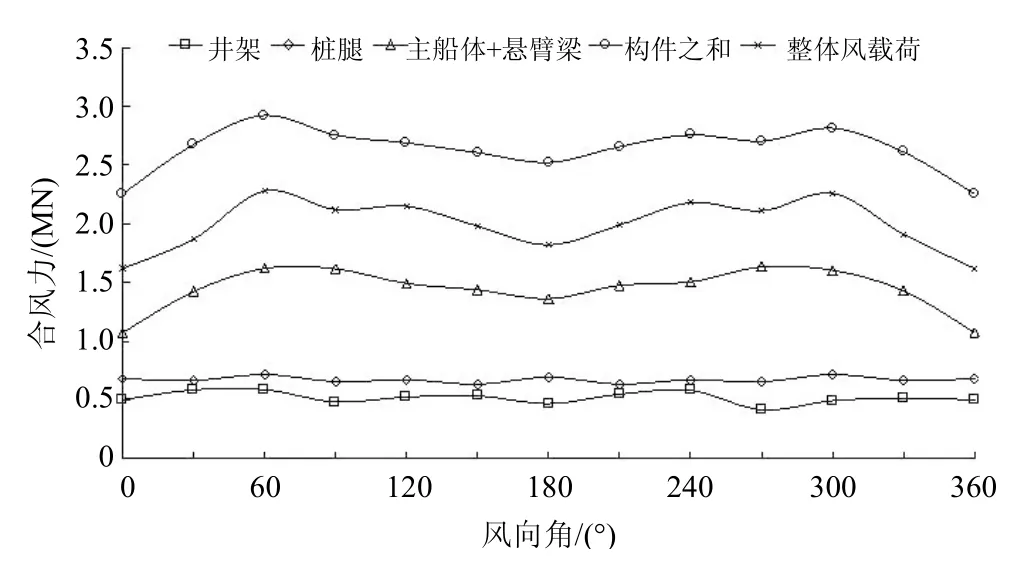
图10 正常作业的干扰现象

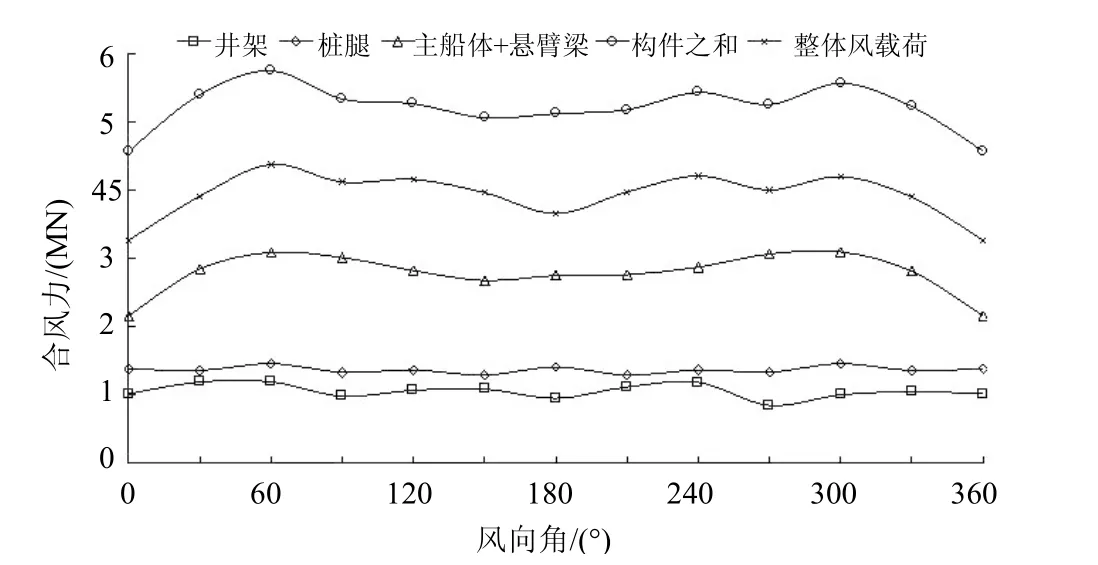
图11 风暴自存的干扰现象

表2 正常作业的空气动力学干扰因子IF

表3 风暴自存的空气动力学干扰因子IF

风洞实验（图10、11）及数值模拟（表2、3）反映了自升式平台在空气动力学干扰下的风载荷变化情况，相比于风洞实验，数值模拟灵活性更大，能分析各构件的干扰现象，这一点是风洞实验做不到的。结果表明，风洞实验和数值模拟在干扰因子的计算上吻合良好，其值在0.7～0.8左右，但在120°和150°上偏差略大。

风洞实验和数值模拟均表明，正常作业和风暴自存状态下的IF值几乎相同，最大差别不超过1.5%，可以认为风速对空气动力学干扰的影响很小。

3.3 流场分析

图12为平台的风速矢量图，不难发现结构之间的干扰非常明显。没有其他结构干扰时，风吹过结构表面在迎风面两侧分离于结构后方形成漩涡；当有干扰时，风在经过上风向结构后在其侧面发生分离，下风向的风速度矢量密度减少，因此干扰对下风向结构表面的风压有明显的缓解作用。

图12 风速矢量图对比

4 结 语

本文以122m自升式平台为例，采用求解RANS方程的方法，结合VOF方法和kε-湍流模型对风载荷的空气动力学干扰现象进行数值模拟，并与风洞实验结果进行比较分析，研究表明：

1) 现行规范进行海洋平台风载荷计算时不考虑空气动力学干扰，风洞实验及数值模拟结果表明，这样的处理方法将导致计算结果偏于保守。

2) 数值模拟结果与风洞实验结果吻合良好，而且具有灵活性好、可视化强的特点，可作为平台设计时风载荷计算的辅助手段。

3) 平台整体的干扰因子在0.7～0.8左右，其中遮蔽效应占主导位置。井架受到遮蔽干扰影响较小，桩腿受到遮蔽效应影响较大。对于平台整体而言，风速对空气动力学干扰的影响很小。

[1] American Bureau of Shipping, ABS Rules for Building and Classing Mobile Offshore Drilling Units 2010, part 3-Hull Construction & Equipment[S], 2010.

[2] H.Boonstra, Ingenieursbureau. Anlysis of full Scale Windforce on a Semisubmersible Platform Using Operator Data[Z]. 1979.

[3] Egon T. D. Bjerregaard and Svenn Velschous. Wind Overturing Effect on a Semi-dubmersible[Z]. 1978.

[4] 朱 航，马 哲，等. HYSY-981半潜式平台风载荷数值模拟与风洞实验[J]. 船海工程，2009，38(5): 149-152.

[5] 朱 航，马 哲，等. 梯度风作用下HYSY-981半潜式平台风载荷与表面风压分布研究[J]. 中国海上油气，2010，22(4):270-274.

[6] Blessmann J.Buffeting Effects of Neighboring Tall Buildings[J]. Journal of Wind Engineering and Industrial Aerodynamics,1985, (18): 100-105.

[7] 巩 雪，翟钢军. 深水半潜式平台风载荷体型系数风洞试验研究[J]. 中国海洋平台，2010，25(5)：29-32.

[8] 王 健，李海涛. 计算流体力学方法在船舶领域的实用性研究[J]. 船舶与海洋工程，2012, (4): 6-11.

[9] 侯爱波，汪梦甫. 建筑数值风洞的基础研究[J]. 湖南大学学报，2007，34(2)：21-24.

[10] Khanduri A.C.Stathopoulos T.Bedard C. Wind-induced Interference Effects on Buildings-a Review of the State-of-the-art[J].Engineering Structure,1998, 20(7): 617-630.