基于半正定约束的最差性能最优通用信号模型顽健波束成形算法
徐定杰,贺瑞,沈锋
(哈尔滨工程大学 自动化学院,黑龙江 哈尔滨 150001)
1 引言
自适应波束成形技术广泛应用于雷达、通信、声呐、声学以及医学成像等众多领域。在阵列导向矢量和协方差矩阵准确已知的情况下,自适应波束成形器能输出最优的信号干扰噪声比(SINR)。但在实际应用中,由于阵列校正误差、未知传感器互耦、近场波前失真、源扩展、相干和非相干的局部散射以及有限的采样数据等因素的影响,使得实际的阵列导向矢量和协方差矩阵与其理想值之间存在误差,严重影响了波束成形器的性能。
目前,研究者已经提出了很多顽健的自适应波束成形方法来解决上述问题,但这些算法大多是针对简单的点信号源模[1~10]。而在一些实际应用中,如无线通信和声纳,由于相干和非相干散射(空间分布)或波前扰动的作用,天线阵列不能再将这些信号源作为点信号源,应当建模为具有一定中心角和角度扩展的空间分布式信号源。此时,需要利用高秩信号模型来描述信号散射和波前扰动的影响,而且通常利用信号的协方差矩阵来描述期望信号的阵列响应,而不是期望信号的导向矢量。因此,多数算法不能直接推广到高秩信号模型。针对通用信号模型,文献[11]提出了一种具有闭环形式解的顽健自适应波束成形算法,通过使期望信号和接收信号的协方差矩阵对所有可能的失配维持无畸变响应从而提高顽健性,即所谓的最差性能最优。但是求解过程中没有考虑协方差矩阵的半正定特性,只是限制了失配约束参数必须小于协方差矩阵的最大特征值,而最优解的求取必须借助于约束参数。因此可能导致所求的解过于保守,无法获得最优解。文献[12]提出了一种基于迭代的顽健自适应波束成形算法,该算法附加了协方差矩阵的半正定约束,因此算法的性能有所提高。但是基于半正定规划的问题必须在每次迭代中由内点方法求解,大大增加了算法的计算复杂度,制约了算法的实际应用。
本文针对通用信号模型,提出了一种新的顽健自适应波束成形算法。该算法基于期望信号和接收信号协方差矩阵的最差性能最优,并且考虑了协方差矩阵的半正定约束。通过对波束成形器进行建模和变换,得到了一种新的顽健自适应波束成形器的表达式,并且通过对波束成形器进行求解,得到了最优权矢量的近似闭式解,相对于文献[12]中的迭代求解具有较低的计算复杂度并且更加接近于最优值。
2 通用信号模型
考虑一个传感器阵列是由M个阵元组成的理想均匀线阵,则 1M×维的阵列接受信号为

其中, s( k)、 i( k )和 n ( k)分别表示统计独立的期望信号、干扰信号和噪声组成部分。阵列输出为y( k ) = wHx ( k ),其中, w = [ w , w , ⋅ ⋅ ⋅,w]T为加权
0 1M-1矢量, (⋅ )T和(⋅)H分别表示矩阵的转置和共轭转置。阵列加权矢量w可以通过最大信干噪比准则获得

其中,
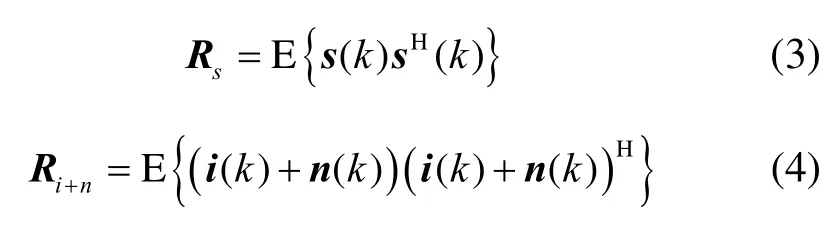
分别为阵列期望信号的协方差矩阵和干扰加噪声协方差矩阵。在点信号源模型下,期望信号s( k ) = s0( k)as,期望信号协方差矩阵其中, s0( k)为期望信号波形,为s0( k)的协方差,as为期望信号的导向矢量。在这种情况下,sR的秩为1,并且式(2)可以简化为
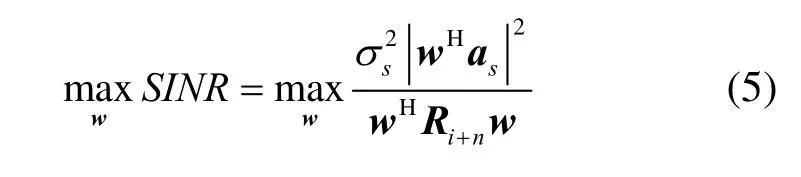
但在一些实际应用中,如无线通信和声呐中的非相干散射(空间分布)或具有波前扰动的信号源,天线阵列不能将这些信号源作为点源,应当建模成具有一定中心角和角度扩展的空间分布式信号源。在这种情况下,不能简单地利用信号的导向矢量建模,sR可以表示为[13]

其中, ρ ( θ)为信号源空间角功率密度函数。因此,通用信号模型可以为点信号源或空间分布式信号源,称 Rs为通用信号模型的协方差矩阵,它的秩为1到M之间的任意整数。通用信号模型下自适应波束成形算法可以表示为[11]

则自适应波束成形算法的最优权矢量optw 为

其中, p { ⋅}表示求矩阵的主特征矢量,即对应于最大特征值的特征矢量。
3 最坏情况下顽健自适应波束成形算法
在实际波束成形应用中,很难得到协方差矩阵sR和in+R 的真实值,一般用协方差矩阵的估计值和误差来表示真实的协方差矩阵,假定具有如下关系
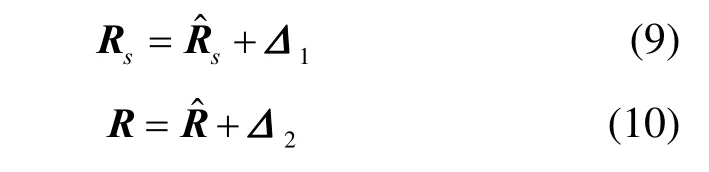
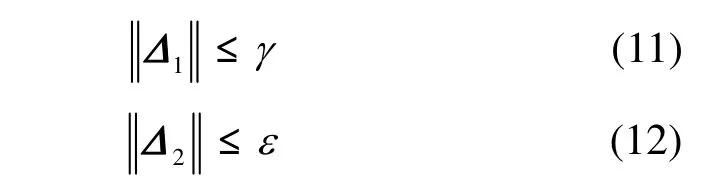
为了改善对于任意失配的顽健性,保证在最差失配条件下的无失真响应,基于最差性能最优的顽健波束成形算法可以表示为

该波束成形算法可以描述为在最差失配2Δ条件下保持期望信号的无失真阵列响应,同时在最差失配1Δ条件下的阵列输出功率最小,因此该算法是基于最差性能最优准则的。通过文献[11]中的处理方法,该问题可以简化为
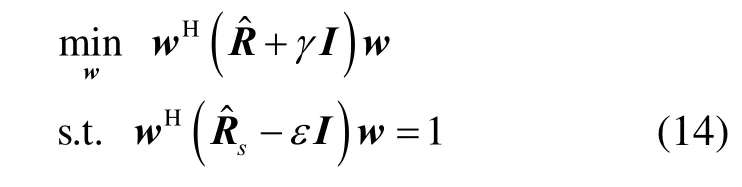
利用Lagrange乘数方法进行求解,该波束成形算法的最优解为
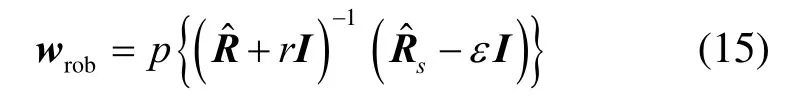
4 基于半正定约束的顽健自适应波束成形算法
由于算法(13)没有考虑协方差矩阵的半正定约束,可能导致所求的解过于保守。因此,提出了一种基于半正定约束的顽健自适应波束成形算法


则式(16)可以等价的转化为

其中,η为Δ的模约束参数且0η>。
5 顽健波束成形算法的求解
为了对式(18)进行求解,首先要求解以下最小化问题

把目标函数展开,式(19)可转化为

对于该最优化问题,最优解显然取在约束集合的边界上,因此不等式约束可以等价转换为等式约束也可以表示为

对于该等式约束最优化问题,可以利用Lagrange乘数方法进行求解,其解可通过最小化如下函数获得

其中,λ为Lagrange乘数。求式(22)关于Δ的梯度并令其为零,得
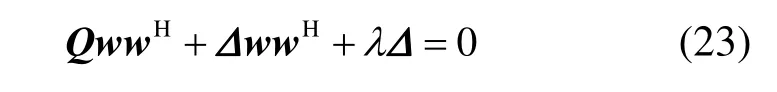
可得Δ的最优解为

运用矩阵求逆引理,式(24)可重新写为

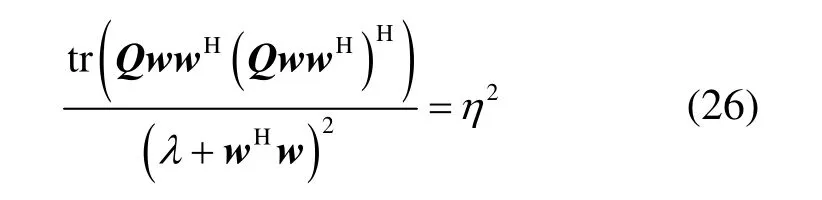
其中, tr (⋅)表示迹运算。由式(25)和式(26),可以得到最差情况下的值,即
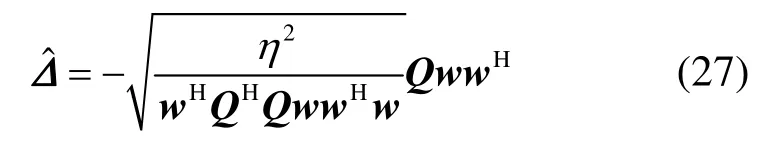

则最优化问题(18)可以等价转换为

由于约束的括号中含有未知的参数w,因此很难利用Lagrange乘数方法求得最优的闭式解。由于=QHQ,则式(29)中的约束可等价地转化为


即

则最优化问题(29)可近似为

由式(32)可以看出,新约束条件比原来的约束更为严格。可以证明,最优解发生在不等式约束的边界上,因此式(33)与式(15)具有相似的形式,与文献[11]中的求解方法类似,利用Lagrange乘数方法进行求解,该顽健自适应波束成形算法的最优解为

6 仿真分析
为了验证所提出算法的顽健性、求解的正确性,进行了如下的仿真实验。考虑阵元数为20,阵元间隔为半个信号波长的理想均匀线阵。假设期望信号和干扰信号都为非相干散射源,其角功率密度分别服从高斯分布和均匀分布,中心波达方位角分别为30°和 30-°,方位角角度扩展方差都为4。假定期望信号的角功率密度也服从高斯分布,但中心波达方位角和角度扩展方差分别为32°和6。此外,干扰信号功率和空间白噪声功率分别为20dB和0dB。所有的实验结果均由200次Monte-Carlo实验平均所得,并将其与对角加载算法LSMI (diagonally loaded sample matrix inversion)、文献[11]和文献[12]提出的进行比较。其中,对角加载因子 30r= ,模约束参数ε和η分别设为文中使用MATLAB CVX工具箱对文献[12]中的迭代算法进行求解。
图1给出了不同输入SNR对输出SINR性能的影响。显然,本文提出的方法和文献[12]中的算法要优于文献[11]中的算法,这是由于附加了协方差矩阵的半正定约束,提高了算法的性能。而本文提出的方法又要优于文献[12]中的迭代算法,这是因为本文提出的方法得到了权矢量的闭式解,该解更加接近权矢量的最优解。随着 SNR的增加,只有LSMI算法的输出SINR增加缓慢,并且性能最差。
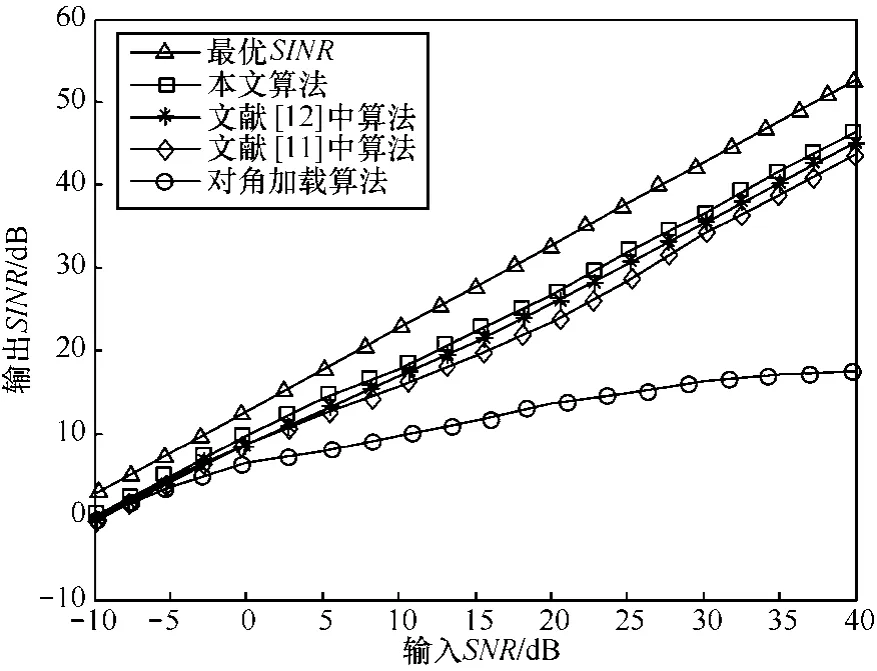
图1 输出SINR相对于输入SNR的变化
图 2给出了不同快拍数对波束成形器输出SINR的影响。从图中可以看出,本文提出的方法在快拍数变化时有着比较稳定的输出SINR,并且优于文献[11]和文献[12]中算法的性能。同样,由于附加了协方差矩阵的半正定约束,文献[12]中算法输出的SINR要高于文献[11]中的算法。LSMI算法输出的SINR最低,逐渐接近15dB。

图2 输出SINR相对于快拍数的变化
7 结束语
针对传统波束成形算法在通用信号模型下的局限性,提出了一种基于半正定约束的通用信号模型顽健波束成形算法。该算法利用协方差矩阵的半正定约束,提高了算法的顽健性。通过对波束成形器进行变换和求解,得到了最优权矢量的近似闭式解,具有较低的计算复杂度。计算机仿真结果也验证了所提算法的正确性和有效性。
[1] TIAN Z, BELL K L, VAN TREES H L. A recursive least squares implementation for LCMP beamforming under quadratic constraint[J].IEEE Transactions on Signal Processing, 2001, 49(6): 1138-1145.
[2] LI J, STOICA P, WANG Z S. On robust capon beamforming and diagonal loading[J]. IEEE Transactions on Signal Processing, 2003,51(7):1702-1715.
[3] LI J, STOICA P, WANG Z S, et al. Doubly constrained robust capon beamformer[J]. IEEE Transactions on Signal Processing, 2004, 52(9):2407-2423.
[4] VOROBYOV S A, GERSHMAN A B, LUO Z Q. Robust adaptive beamforming using worst-case performance optimization: a solution to the signal mismatch problem[J]. IEEE Transactions on Signal Processing, 2003, 51(2):313-324.
[5] FELDMAN D D, GRIFFITHS L J. A projection approach to robust adaptive beamforming[J]. IEEE Transactions on Signal Processing,1994, 42(4):867-876.
[6] BECK A, ELDAR Y C. Doubly constrained robust capon beamformer with ellipsoidal uncertainty sets[J]. IEEE Transactions on Signal Processing, 2007, 55(2):753-758.
[7] CHEN C Y, VAIDYANATHAN P P. Quadratically constrained beamforming robust against direction-of-arrival mismatch[J]. IEEE Transactions on Signal Processing, 2007, 55(8):4139-4150.
[8] LIU W L, DING S X. An efficient method to determine the diagonal loading factor using the constant modulus feature[J]. IEEE Transactions on Signal Processing, 2008, 56(12):6102-6106.
[9] HASSANIEN A, VOROBYOV S A, WONG K M. Robust adaptive beamforming using sequential quadratic programming: an iterative solution to the mismatch problem[J]. IEEE Signal Processing Letters,2008, 15:733-736.
[10] LIU C F, LIAO G S. Robust capon beamformer under norm constraint[J]. Signal Processing, 2010, 90(5):1573-1581.
[11] SHAHBAZPANAHI S, GERSHMAN A B, LUO Z Q, et al. Robust adaptive beamforming for general-rank signal models[J]. IEEE Transactions on Signal Processing, 2003, 51(9):2257-2269.
[12] CHEN H H, GERSHMAN A B. Robust adaptive beamforming for general-rank signal models using positive semi-definite covariance constraint[A].Proc IEEE ICASSP[C]. Las Vegas, USA, 2008.2341-2344.
[13] 王永良, 陈辉, 彭应宁等. 空间谱估计理论与算法[M]. 北京: 清华大学出版社,2004.WANG Y L, CHEN H, PENG Y N, et al. Spatial Spectrum Estimation Theory and Algorithm[M]. Beijing: Tsinghua University Press, 2004.

