基于BP神经网络的边坡稳定性分析*

郭钟群，余金勇，彭道强，吴 广

(1.江西理工大学，江西 赣州 341000;2.江西铜业集团公司德兴铜矿，江西 德兴 334224;3.深圳天华建筑设计有限公司，广东 深圳 518040)

1 引言

边坡的稳定性一直是岩土工程界研究的重点、热点问题。随着我国经济建设的不断推进，在工程建设领域涌入了大量的边坡问题，如在矿山工程、道路铁道工程、水利港口工程等领域出现大量的高陡边坡[1]。边坡一旦失稳破坏会给人民的生命财产安全以及国家的经济建设带来不可估量的损失，如何安全有效地准确评价边坡的稳定性有重大的现实意义。

由于边坡岩土体的地质环境复杂以及受多种因素共同作用，使得边坡稳定性分析存在明显的不确定性——模糊性和随机性，传统的分析方法并不能有效地解决边坡的不确定性问题，因此运用不确定性评价方法对边坡稳定性进行评价是切实可行和十分有效的[2]。本文利用BP神经网络理论对德兴铜矿黄牛前边坡进行分析评价，结果与实际情况相符，说明该方法对指导实际工程有重要作用。

2 边坡稳定性分析方法

2.1 定性评价分析方法

定性评价分析方法通常也叫“非数量分析法”，其主要特点是:通过工程地质勘察报告，工程师根据以前研究案例和个人丰富实践经验以及主观的判断和分析能力对边坡影响因素进行分析以及对边坡可能的变形破坏模式或失稳机制进行预测。通常包含以下几种方法:自然 (成因)历史分析法、工程类比法[3]、SMR 分析法[4]、几何图解法[5]等。这些方法的主要优点是可以综合考虑多种影响因素的影响，并且能够讯速地判断边坡的稳定状态。

2.2 定量评价分析方法

定量评价分析方法也称为“数学模型法”，边坡稳定性定量评价是以地质资料分析为前提，将复杂繁琐的模型经过合理的简化，并将所得数据资料代入简化的模型进行定量计算，从而得出评判结果。定量评价的关键问题是模型的如何简化和参数的如何选取，因为太过简化的模型不能够客观真实地反映实际状况，而太过复杂的模型即便是考虑的因素全面，但是会由于本构关系或者提取参数的可信度影响，使得研究问题的结果不能客观地反映真实情况，失去意义。目前只有极限平衡分析方法[6]和数值分析[7]方法应用最为广泛和普遍。

2.3 不确定性分析评价方法

由于边坡的稳定性受大量的因素共同影响决定的，这些影响因素有些是包含一些定量因素和一些定性因素和人为因素，而且组成边坡的岩体是多样性的，地质环境复杂多变、多种因素的随机性导致边坡的稳定性分析带有很强的不确定性。传统的分析方法往往不能取得令人满意的结果，所以国内外许多学者通过引入一些新理论和交叉学科，更客观地对边坡的实际情况做稳定性评价。如可靠度分析方法[8]、模糊综合评价分析方法、灰色理论[9]分析方法以及神经网络分析方法，此类方法在边坡稳定性评价中得到了较理想的应用成果，使得不确定性评价方法成为边坡稳定研究的热点[10]。

3 神经网络的基本原理

3.1 BP神经网络概述

神经网络是由大量的神经元组合而成的，神经元是神经网络最基本的单元。神经网络对信息的处理功能主要由神经元的输入输出、神经元的阀值、连接权的大小、网络的拓扑结构共同作用的。

BP神经网络往往也被称为误差反向传播神经网络(Error Back Propagation Neural Network)，该网络是目前发展最为成熟、应用最普遍的神经网络模型，其中绝大多数的网络均选取BP网络模型或者它的变化形式[11]。BP网络是一种多层前馈神经网络，由输入层、一个或多个中间层(隐含层)以及输出层组成，所以它至少具有三层或以上的网络构成。其结构和学习过程见图1。

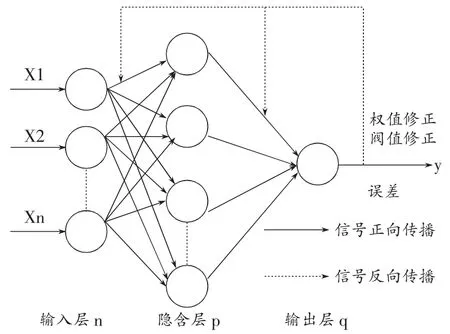
图1 BP神经网络的结构和学习过程

3.2 BP神经网络算法步骤

BP算法的本质内容是求解误差函数的最小值问题，其主要思想是把学习过程分为输入信号的正向传播及其训练误差的反向传播两个步骤，其中正向传播过程为把一对学习样本传输给网络，由输入层传输到中间层各神经元，再通过中间层各神经元逐个处理后传到输出层逐层更新，网络的每前一层的输出值将作为后一层网络的输入值，也称为前向传播过程;如果网络的实际输出值与期望输出值一致，那么该学习样本学习结束并对下一个样本进行学习;如果网络的实际输出值与目标输出值并不一致，那么该网络将转入误差的反向传播阶段，网络按照减少期望输出与实际输出之间的误差方向，由输出层开始以某种方式逐层向前传播，并将误差分摊给所有神经元，并调整神经元之间的连接权值，最后回到输入层，这种算法叫做“误差的逆传播算法”。经过周而复始的调节，不断调整神经元之间的连接权值，直到输出误差满足精度要求为止，停止学习[12]。BP神经网络算法流程图如图2所示。

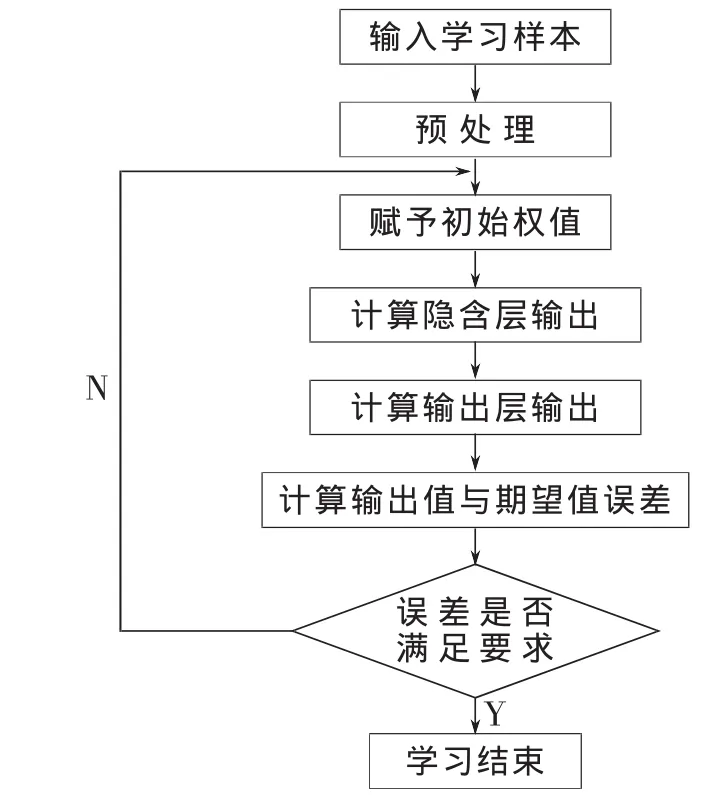
图2 BP神经网络算法流程图

4 工程应用

德兴铜矿位于江西省德兴市，是我国有色矿山中最大的露天矿，地处怀玉山北麓，多山地丘陵，矿藏储量大并且集中，埋藏较浅，剥采比小，同时综合利用元素较多，还有金、银、钼等多种稀有元素。随着三期工程建设和挖潜改造工作的推进，矿山开采规模已达10万t/日，年采剥总量达6400多万t。铜厂矿区黄牛前、杨桃坞、水龙山、石金岩和西源岭开采阶段边坡已形成，且边坡暴露高度最高达400多m，根据设计，部分区域最终边坡高度将超过700m，其边坡范围与边坡高度在国内是处于前列的。

在矿山开采过程中，由于岩体自重应力、断层、节理等地质构造以及爆破震动、地下水等各方面因素的影响作用，部分区段的边坡已出现局部不稳定现象。本文以黄牛前边坡为例，分析其边坡稳定性。从文献[13－14]中收集42个边坡实例作为学习样本，输入向量选取对边坡稳定影响较大的因素:岩土体容重、粘聚力、内摩擦角、边坡角和坡高以及孔隙压力比等，输出向量选取边坡安全系数和边坡稳定状态，对于边坡稳定状态1表示稳定，0表示破坏。学习样本中36个作为训练样本，6个作为检测样本，以此来测试网络的性能，将训练好的网络运用于“黄牛前”边坡，得出该边坡得出稳定状态。部分训练样本如表1所示。

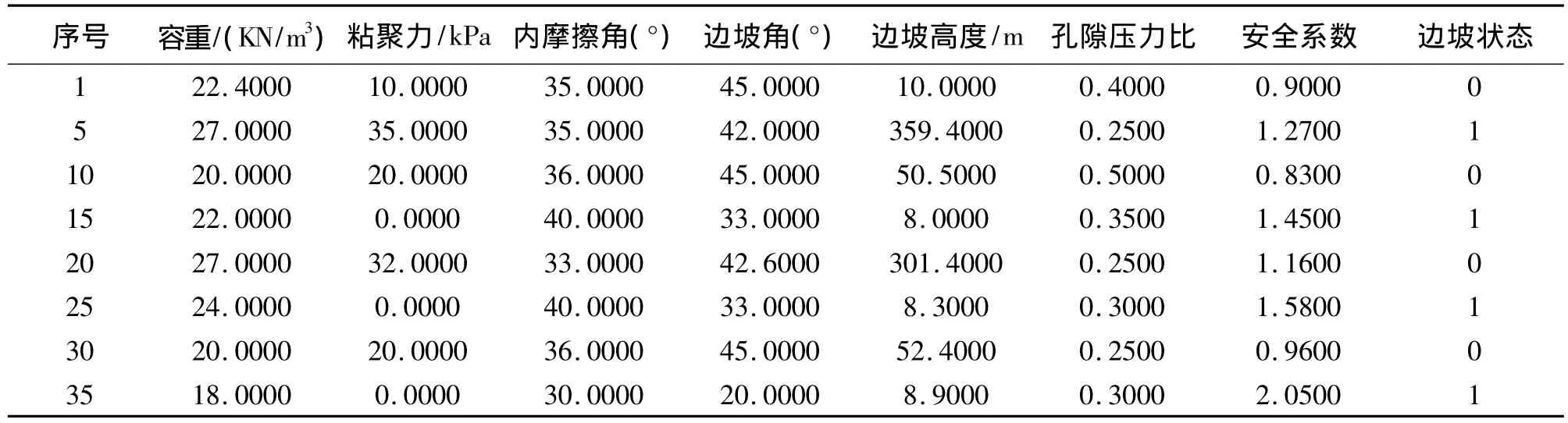
表1 边坡稳定性训练样本

为了提高网络的精度和消除参数量纲之间的影响以及加快网络训练速度，需要对学习样本进行归一化处理。由于孔隙压力比的范围在区间[0，1]之间，对其影响太小故不需要对其进行归一化，归一化后的样本见表2。选取6个检测样本见表3。

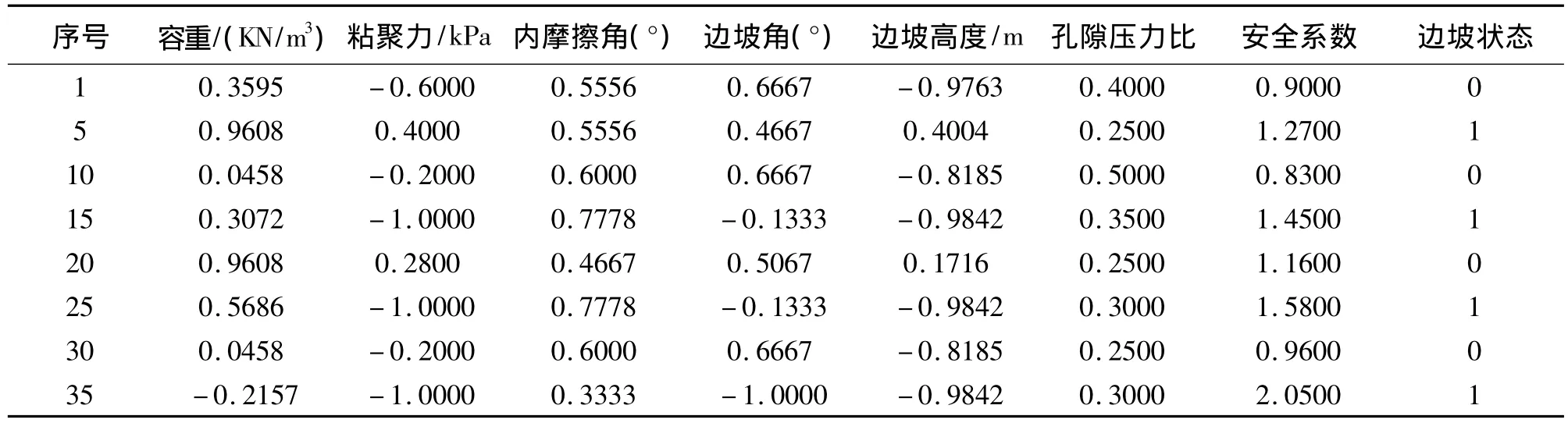
表2 归一化处理后的训练样本

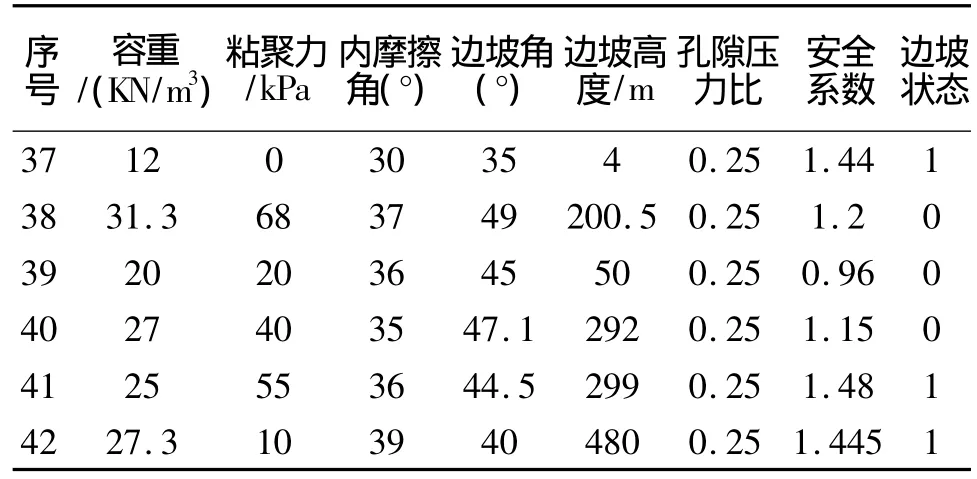
表3 检测样本数据

使用Matlab7.0的神经网络工具箱，选择BP网络对学习样本进行反复训练，建立学习样本的输入向量与输出向量之间的非线性关系。训练结果表明:选用11个中间隐含层节点的训练效果最佳，其中传递函数均选用‘tansig’，训练函数选用自适应学习速率的梯度下降法‘traingdx’，最大训练次数为15000 次，训练精度为 0.001，学习率为 0.05，其他参数均选用默认值。选用6－11－2的模型对表2和3分别进行训练和仿真，经过11470步的训练，网络已经收敛，误差满足设置要求。网络训练好后，用检测样本预测网络性能，把边坡系数安全目标值与网络预测值进行对比见表4和图3。

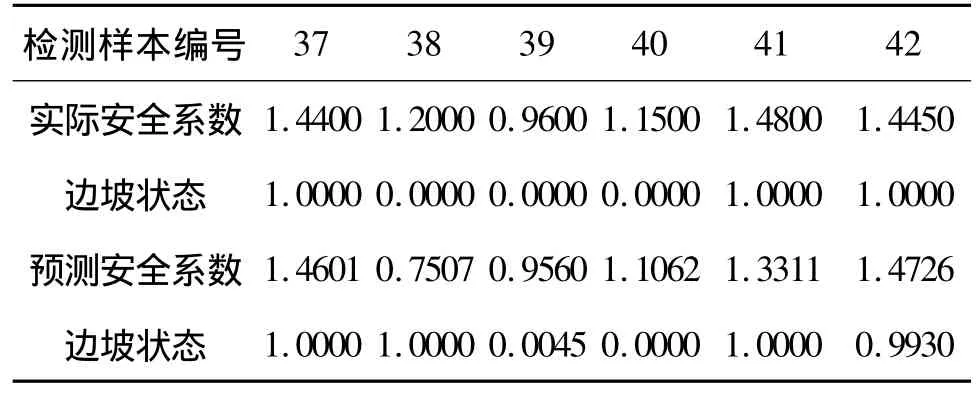
表4 检测样本实际值与预测值

图3 安全系数目标值与网络预测值对比图

由图3可知，经过对学习样本的训练和选取合理的参数，通过对检测样本安全系数目标值与网络预测值对比，可以发现仿真结果与实际结果是比较接近的，其中有5个是正确的，二者结果相差很小，样本38的判定结果是错误的，网络的正确判断率为83.33%。综合起来，神经网络的性能还是得到了比较好的体现，可以应用于工程实例，把上述训练好的网络模拟“黄牛前”边坡，经网络模拟得出安全系数为1.0689，边坡状态为破坏与实际情况一致，对指导实际工程有很大作用。

5 结论

由于我国现代经济建设的需要，在工程建设论域出现了大量的高陡边坡，而边坡一旦失稳破坏，将会对人们的生命财产安全以及经济发展带来不可估量的损失。因此，需要对存在的边坡进行稳定性分析，并对潜在不稳定的边坡进行合理的治理，减少滑坡灾害的发生。本文针对“黄牛前”边坡，考虑了岩性、岩体结构等多种影响边坡稳定性的影响因素，利用BP神经网络对学习样本的训练，建立输入向量与输出向量的非线性关系，将训练好的网络预测“黄牛前”边坡的安全系数与评价边坡状态，结果符合现场实际情况。

[1]孙玉科，姚宝魁.我国岩质边坡变形破坏的主要地质模式[J].岩石力学与工程学报，1983(01):12－16.

[2]冯夏庭，王泳嘉，卢世宗.边坡稳定性的神经网络估计[J].工程地质学报，1995(04):145－151.

[3]周海清，刘东升，陈正汉.工程类比法及其在滑坡治理工程中的应用[J].地下空间与工程学报，2008(06):97－101.

[4]Romany M.SMR classification[M].In Proe.7th ISRM Congress，1991:955－960.

[5]郑文晓，吴平.图解法在地质灾害评估中的应用[J].西部探矿工程，2008(03):16－21.

[6]皱广电，魏汝龙.土坡稳定分析普遍极限平衡法数值解的理论及方法研究[J].岩石力学与工程学报，2006(02):146－150.

[7]王晓东，陈守龙.路基边坡稳定性有限元数值分析[J].安徽建筑，2011(01):17－18.

[8]邰中勇.滑坡稳定性可靠度分析方法及应用[J].人民长江，2011(22):32－34.

[9]冯勤生.边坡岩体变形灰色预测研究[J].内蒙古科技大学学报，2011(03):196－198.

[10]王东，袁景.边坡稳定性分析中不确定性方法的评价[J].辽宁工程技术学报，2005(s2):4－7.

[11]童树奇.人工神经网络在边坡工程中的应用研究[J].广东土木与建筑，2006(09):25－29.

[12]何方维，朱明，刘文生，等.BP网络在露天矿边坡角优化中的应用[J].灾害学，2001(01):35－40.

[13]付义祥，刘世凯，刘大鹏.RBF神经网络在边坡岩体稳定性中的预测研究[J].武汉理工大学学报，2007(02):170－174.

[14]侯殿昆，宋秀琴，吴登军.基于神经网络的多参数露天边坡稳定性分析[J].辽宁工程技术大学学报，2007(05):649－652.