大连星海湾跨海大桥主桥动力模型设计

钟 慧，檀永刚

（大连理工大学 桥梁工程研究所，辽宁 大连 116023）

悬索桥在最近的30年里得到了蓬勃的发展，其跨径能力大、抗震性能好、轻型美观，已成为大跨度桥梁的首选［1］.其结构主要包括主缆、吊杆、桥塔、锚碇及加劲梁.悬索桥的结构和边界条件都比较复杂，且某些部位的局部应力问题也较为突出，数学模型不可能准确模拟悬索桥结构的各种重要物理力学现象，或者模拟还有困难［2］.因此往往采用简化计算的办法，这样就扩大了计算模型与实际结构之间的差距，这时一般要通过模型试验来检验简化方法的可靠性与精度.模型试验历史悠久，早在1755年，德国工程师格莱伯曼为了在莱茵河上修建木桥就首先使用模型验证了设计的可靠性；1846年，英国罗伯特、斯坦福森等为修建不列颠桥设计进行了1／6的桥梁结构模型试验［3-4］.

本文依托星海湾特大悬索桥为工程背景，依据相似原理设计了1／50的全桥模型，通过试验测得了模型结构的动力参数，并建立了模型的三维空间有限元模型与实测结果相比较.

1 工程概况

大连市南部滨海大道主桥为三跨地锚式悬索桥，桥跨布置为180m＋460m＋180m；加劲梁为双层钢桁架结构，主桁架桁高10m，标准节段长10m；主缆由多股平行钢丝成品索组成，横桥向间距为25.2m；全桥共有79对吊杆，吊杆间距为10m；桥塔全高111.81m；两端设混凝土重力式锚碇.全桥总体立面布置如图1所示.

图1 全桥总体立面布置图（单位：cm）Fig.1 Elevation of the Xinghai Bay Bridge（Unit：cm）

2 试验模型的设计

2.1 试验模型的总体设计

本模型严格按照相似原理［5］制作，考虑模型试验目的、实验室空间、试验加载空间、测试精度、制作能力等因素，结合本桥特点，几何缩尺选用λl＝1／50.

加劲梁主要承受轴力的作用，其模拟主要考虑横向刚度及竖向刚度.采用铝合金制作，各杆件严格按照相似比设计，用铆钉连接.为了满足质量分布的相似条件，主桁采用钢板进行配重，上桁采用规格为488mm×398mm×8mm的钢板，共82块，下桁采用规格为460mm×398mm×8 mm的钢板，共82块.

桥塔也选用铝合金材料制作，其几何尺寸按照相似原则进行设计，塔柱结构形式为轴心受压构件，为保持截面外轮廓尺寸基本不变，桥塔截面为变截面形式，这样模型与实桥的截面面积和惯性矩的相似比得到满足，由于桥塔的配重加载较为困难，没有在模型中施加.

主缆只受拉应力，其模拟主要考虑轴向拉伸刚度的相似，选用直径为0.7mm的钢丝（共两股每股33根），由于主缆的配重的加载较为困难，本模型中也未考虑.主桥模型如图2所示.

图2 星海湾跨海大桥主桥试验模型整体照片Fig.2 Photo of the test model

2.2 动力相似关系推导［6-7］

动力模型的相似关系可根据结构的自由振动公式来分析.结构无阻尼自由振动方程为：

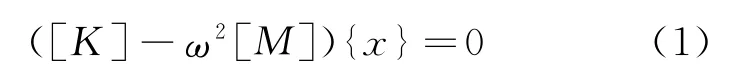
式中，［K］为结构刚度矩阵；［M］为质量矩阵，对于集中质量矩阵其元素为ρAL；｛x｝为位移列阵；ω为角频率；ρ为材料密度.则可得相似准数为

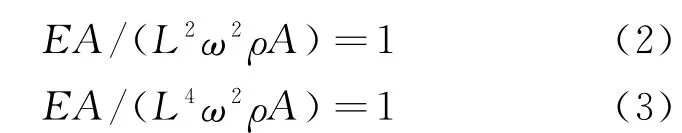
根据静力相似关系，以上两式等价，则可得：

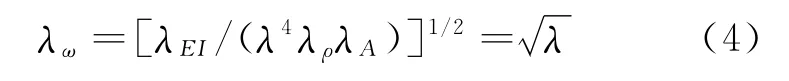
式中，λρ、λω分别为结构密度、圆频率的相似比.此外，对于一般的动力模型，还要考虑以下两个相似准数：ρgL／E＝1和ρaL／E＝1.通常λg＝λa＝1，因此，要求λρ＝λE／λ，这和静力模型中得到的结果相同.

3 悬索桥三维有限元模型的建立

为验证模型的实测结果，本文用MIDAS进行了模型的空间有限元计算.由于动力计算的正确性取决于有限元模型建立是否恰当，其主要影响因素有结构的刚度、质量和边界条件.悬索桥主要受力构件为主缆、桥塔、吊杆、主桁.根据各构件的受力特点，选取合适的有限元单元.本模型用到的主要单元有模拟主桁各构件及桥塔的梁单元，模拟主缆及吊杆的只受拉单元，并将配重通过节点载荷的方式加载到主桁各节点，在做特征值分析时再将载荷转换成质量.有限元计算模型如图3所示.

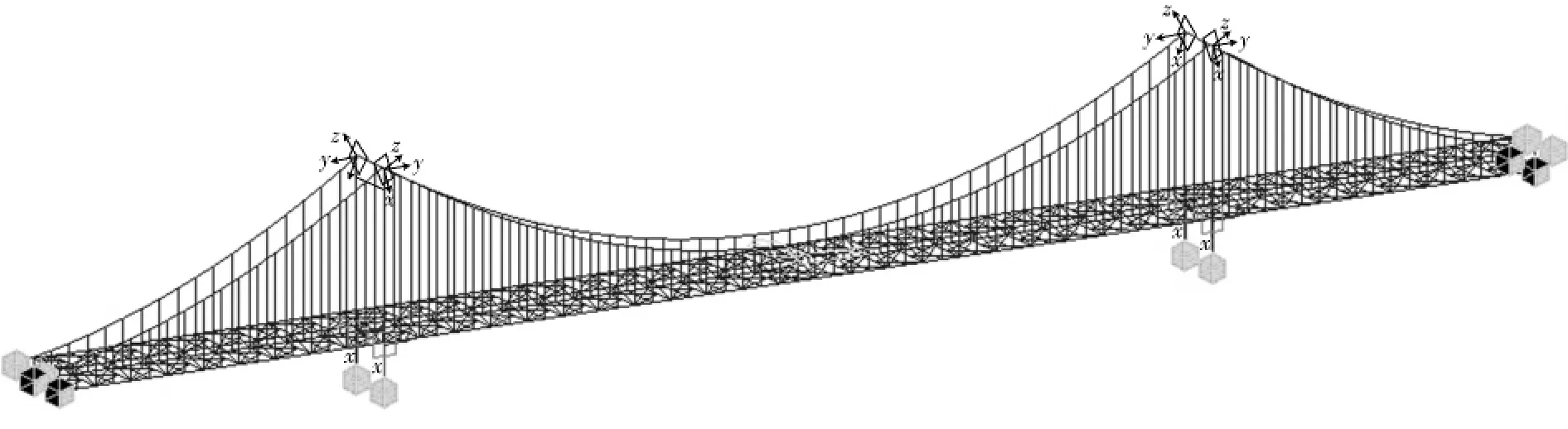
图3 悬索桥的空间有限元模型Fig.3 The space FEM of the suspension bridge

4 模型动力试验

本实验的目标是测得模型的竖弯、横弯的自振频率和振型.各频率通过人为激励获得，具体测点布置见图4所示.

受传感器数量的限制及考虑到桥梁结构的对称性，模态试验分次在主梁上布置传感器.在主梁上布置一组动测点，包括垂直速度传感器3个，其中作为参考点固定位置的传感器1个. 垂直速度传感器布置于主梁中心线，每次采集3个通道的数据.

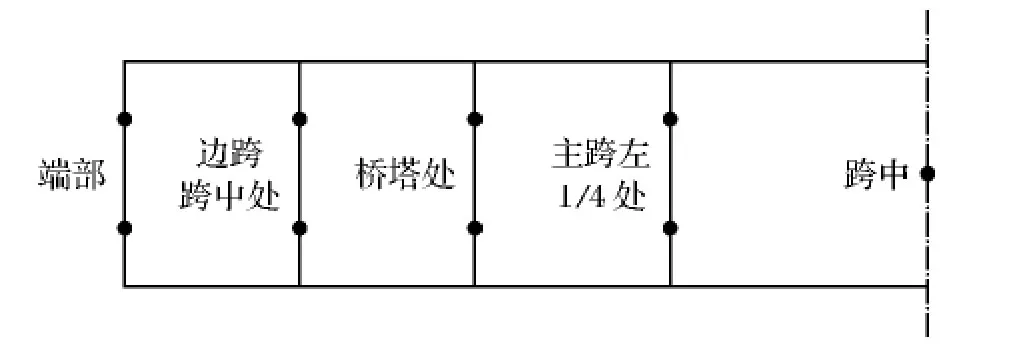
图4 测点布置1／2平面图Fig.4 Half arrangement of measuring points

试验仪器采用东华DH5937数据采集处理系统，测试分析流程如图5所示.

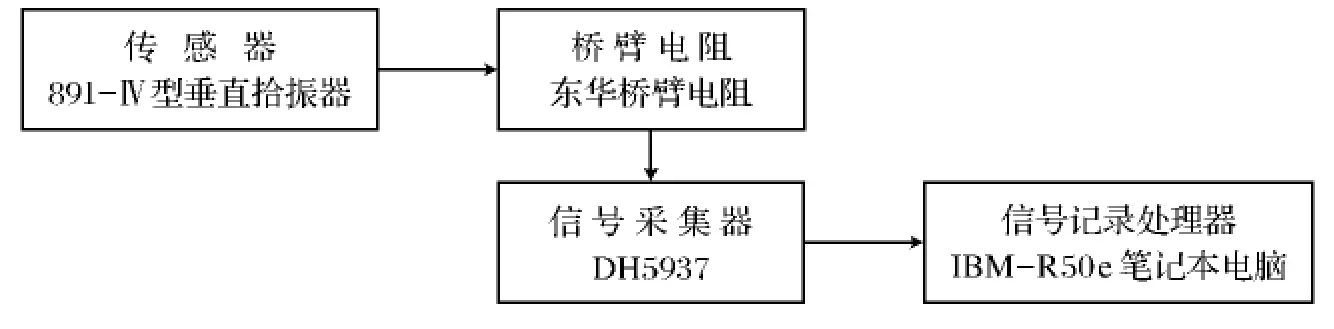
图5 测试分析流程图Fig.5 The flow chat of the test

5 试验结果及分析

根据采集的数据，利用采集系统的分析软件对测点的脉动信号进行了分析，得到了输入点与各个输出点之间的传递函数，经过分析得到各阶模态数值，如图6和图7所示.

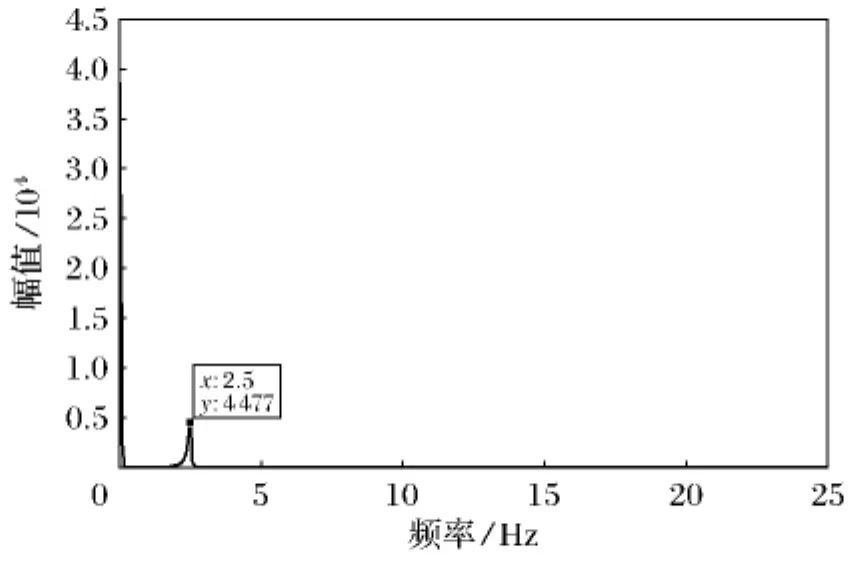
图6 竖弯频域图Fig.6 The frequency of vertical bending

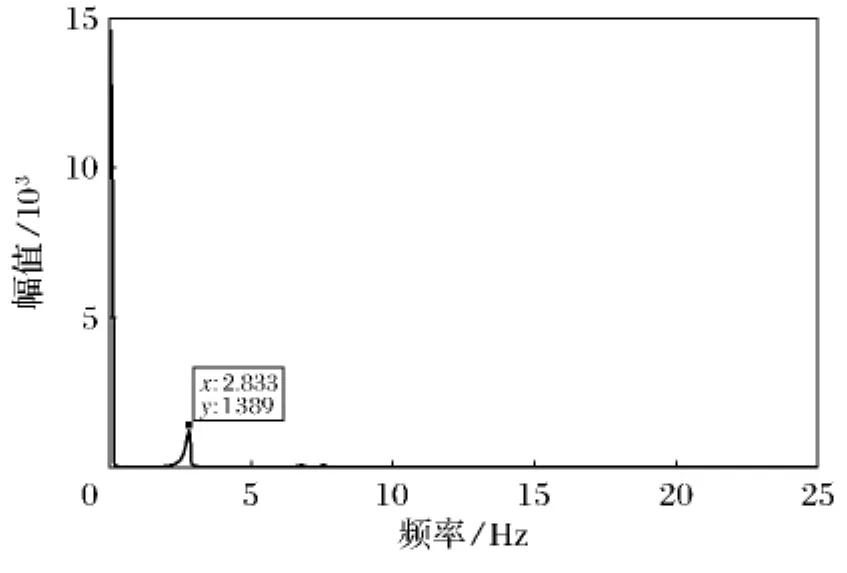
图7 横弯频域图Fig.7 The frequency of transverse bending

由有限元软件MIDAS对桥梁模型进行了理论上的振动模态分析，对比结果见表1.

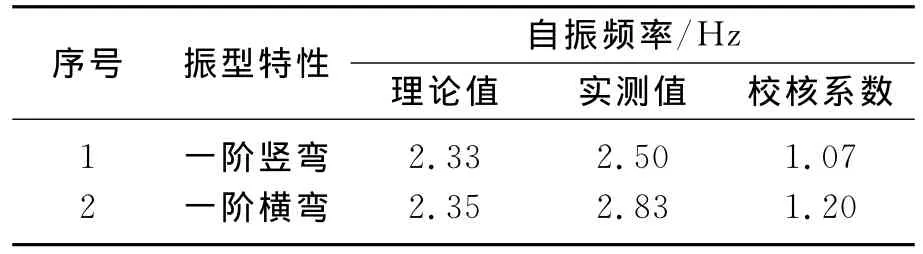
表1 自振频率实测值及理论计算值比较Table1 Comparison of natural frequencies between experimental value and calculated value

从表1可以看出，竖弯频率的实测值与理论值的校核系数为1.07，吻合得很好，横弯的校核系数为1.20，校核系数略大.在模型试验中，质量的配重是以主桁上下各两层钢板均布加载，当人为在横桥向激励时，钢板会随着左右互相错动，导致实测横弯值偏大.而在计算模型中，质量的配重是以质量单元加载在主桁上下弦的节点上，不存在上述现象.在有限元中配重只考虑了其质量的相似并未考虑其横向的刚度效应，由于桥面较宽，导致实测横弯频率值较大.除上述影响因素外，在模型试验中支座的模拟以及吊杆与主缆及主桁的连接无法达到有限元模型中那么理想的状态.测试过程中，加速度传感器本身也有质量，给模型增加了一定的附加质量，对结果也会造成一定的误差.

6 结 论

（1）从模型各阶模态可以反推出实桥动力特性良好.具有足够的刚度来抵抗载荷所产生的变形.表明，实桥所采用的有限位移理论分析其动力特性，并进行抗风、抗震等设计是可靠的.

（2）本次实验测得的各阶模态与理论计算最大误差为20%，对于动力实验来说此结果是比较理想的.个别模态的误差略大，主要原因是缩尺比例太小导致桥梁的细部无法完全真实模拟，特别是支座处的构造.

（3）本次试验中竖弯及横弯频率的实测值与理论值均吻合得较好.表明双梁式计算模型可以应用这种体系的动力分析计算.

（4）有限元中的理想约束，如支座的模拟、吊杆与主桁及主缆的连接以及桥塔与主桁横向的连接在模型试验中无法完全实现，对各阶频率的实测结果有一定的影响.

（5）钢板在人为横向激励时产生的左右错动，使得实测的横弯值较大.在有限元模型中以质量单元模拟配重，未考虑横向的刚度效应，当桥面较宽时，其横弯频率的理论计算值会偏小.

［1］ 周孟波.悬索桥手册［M］.北京：人民交通出版社，2003.（Zhou Mengbo.Suspension Bridge Handbook［M］.Bejing：China Communications Press，2003.）

［2］ 朱宏平，张之勇.悬索桥的动力模型设计与实验［J］.华中理工大学学报：自然科学版，1999，27（3）：26-28.（Zhu Hongping，Zhang Zhiyong.Design and Experiment of a Suspension Bridge Model［J］.Journal of Huazhong University of Science and Technology，1999，27（3）：26-28.）

［3］ 周林仁.大跨度斜拉桥实验室健康监测模型设计与分析［D］.哈尔滨：哈尔滨工业大学，2007.（Zhou Linren.Design and Analysis of Laboratory Health Monitoring Model of a Long-Span Cable-Stayed Bridge［D］.Harbin：Harbin Institute of Technology，2004.）

［4］ 揣民昭，赵柏冬，张亚龙.砂土地基箱形基础基底反力实验研究［J］.沈阳大学学报，2010，22（4）：8-10.（Chuai Minzhao，Zhao Baidong，Zhang Yalong.Sub-grade Reaction of Box Foundation on Sand Sub-grade［J］.Journalof Shenyang University，2010，22（4）：8-10.）

［5］ Ungbhakorn V，Singhatanadgid P.Similitude Invariants and Scaling Laws for Buckling Experiments on Antisymmetrically Laminated Plates Subjected to Biaxial Loading［J］.Journal of Composite Structures，2003，59（4）：455-465.

［6］ 宋广君.琴桥模型试验研究［D］.大连：大连理工大学，2004.（Song Guangjun.Experimental Research of Model on Qin Cable-stayed Bridge［D］.Dalian：Dalian University of Technology，2004.）

［7］ 颜东煌，田仲初，陈常松，等.岳阳洞庭湖大桥三塔斜拉桥全桥静动力模型设计［J］.长沙交通学院学报，1999，15（1）：51-55.（Yan Donghuang，Tian Zhongchu，Chen Changsong，et al.Static and Dynamic Model Design of the Total Bridge of Yueyang Tongting Three Tower Cable-stayed Bridge［J］.Journal of Changsha Communications University，1999，15（1）：51-55.）