基于Copula函数的沪深综指相关性分析

郑 列,郑伦涛,徐 斌 (湖北工业大学理学院, 湖北 武汉 430068)

基于Copula函数的沪深综指相关性分析

郑 列,郑伦涛,徐 斌 (湖北工业大学理学院, 湖北 武汉 430068)

将Copula理论与t-GARCH模型结合在一起，利用各种统计软件作参数估计和检验，通过计算机模拟和计算, 对沪深综指的相关性进行了分析。研究结果表明，沪深综指之间存在很强的正向风险关联性，沪深收益率走势具有相同的方向。

Copula函数；t-GARCH模型；Kendall秩相关系数； Spearman秩相关系数

在对金融资产收益率进行研究时，一个重要的问题是当收益率非正态时，怎么测度股市之间的相关性。在GARCH模型的框架中，一些最新研究都集中在具有厚尾非对称多元分布，比如多远偏态分布,特别是偏态Student-t分布[1]。对于大多数的单变量分布来说，在需要考虑描述相关结构时不可能精确扩展到多变量情形。而且，现在广泛使用的大多数风险管理模型都有这样或那样的缺陷。如很多模型假设多个资产收益序列或风险因子的联合分布服从多元正态分布，但这种假设经常与金融市场的实际情况不相符，故在正态分布假设下进行的资产组合的风险分析和对风险价值VaR(Value at Risk，VaR)的计算与实际情况的误差比较大[2]。为此，笔者引入Copula函数来测度GARCH背景下的条件依赖。Copula函数提供了一种在仅仅已知边际分布时对多元分布建模的有用方法，这种方法在多元分布不是正态分布的情形时特别有用。

1 Copula函数

定义1[3]对所有的t,t∈I=[0,1]，如果一个二元函数C:I2→I，满足：①C(t,0)=C(0,t)=0,C(t,1)=C(1,t)=t；②对任意的u1,u2,v1,v2∈I(u1≤u2,v1≤v2)有:

C(u2,v2)-C(u2,v1)-C(u1,v2)+C(u1,v1)≥0

则称C为(二元)Copula函数。Copula函数是一个边缘在[0，1]上均匀分布的二元分布函数在I2上的限制。

定义2[3]对所有的(u1,u2，…，un)∈In=[0,1]n，如果一个n元函数C:In→I，满足：①C对它的每一个变量都是递增的；②C的边缘分布Ci满足：Ci(ui)=C(1,…,1,ui,1,…,1)=ui，其中ui∈[0,1],i=1,…,n；则称C为n元Copula函数。

考虑随机变量X1和X2，其边际累积分布函数和联合累积分布函数分别为：

Fi(xi)=P(Xi≤xi)i=1,2H(x1,x2)=P(X1≤x1,X2≤x2)

所有的累积分布函数取值区间为[0,1]，在一些情形下，存在多元分布函数，所以函数H(x1,x2)能够得到精确的表达式，像多元正态分布就是如此。然而在很多情况下，边际分布函数Fi(xi)相对来说比较容易求得，它们的联合分布函数H(x1,x2)的精确表达式很难获得。

引理1(Sklar定理[4]) 设随机变量x1,x2,…,xN的联合分布函数是H(x1,x2,…,xN)，边缘分布函数分别是F1(x1),F2(x2),…,FN(xN)，则存在Copula函数C，对任意实数x1,x2,…,xN，有：

H(x1,x2,…,xN)=C(F1(x1),F2(x2),…,FN(xN))

如果Fi(xi)(i=1,2,…,N)是连续函数，则C唯一。

由Sklar定理知道，任何一个n维的分布函数可以被它们的边际分布函数和一个相应的Copula函数唯一确定。

通过Copula函数C的密度函数c和边缘分布F1(x1),F2(x2),…,FN(xN)，可以很容易地求出N元联合分布函数H(x1,x2,…,xN)的密度函数：

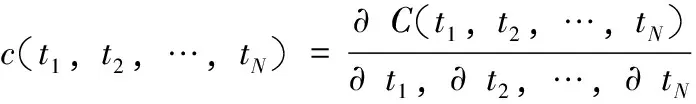
应用Copula函数来对金融数据建模，一般分2步进行：首先要确定边际分布，然后是选择一个合适的Copula函数来测度边际分布的相关性。其中确定边际分布是构建Copula模型的前提。

2 边际分布模型的确定

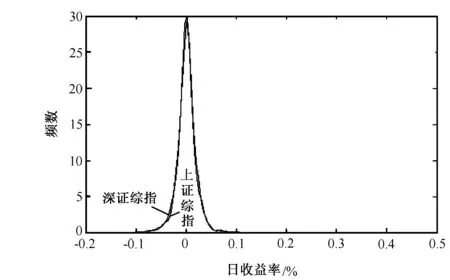
图1 样本密度函数

笔者所使用上海证券交易所的上证综指和深圳证券交易所的深证综指每日收益率数据取自RESSET金融研究数据库(锐思数据)，时间范围是1995-12-08到2011-09-30共17年 (3839个交易日) 的日收益率数据，所用的分析工具是Matlab R2009a。利用Matlab画出样本密度函数，如图1所示。

一般GARCH(1,1)模型就能够满足建模要求，但从图1中可看出分布有厚尾的特性，而t-GARCH过程可以更好的描述时间序列的高峰、厚尾等分布特性，因此在这里选用t-GARCH模型来描述金融收益序列的条件边缘分布。采用极大似然估计法对各收益率序列的边缘分布进行估计,结果如表1所示(表1中各个变量含义见参考文献[3])。

表1 边缘分布模型的参数估计及检验结果

表1中的K-S统计量及其概率值表明，对各序列都不能拒绝零假设：“变换后的收益率序列服从U(0,1)分布”。对变换后的2个序列做自相关检验，可以知道变换后的2个序列均不存在自相关，因而可以将变换后的序列均看成是独立的。K-S统计量和自相关检验表明[3]，根据t- GARCH(1,1)模型估计得到的边缘分布，对原序列做概率积分变换后得到的序列均服从独立同分布U(0,1)。说明t- GARCH(1,1)模型可以比较好地拟合2个序列的边缘分布，用它来描述它们的收益率序列的边缘分布是恰当的。

另外，对于t分布来说,t分布尾部的形状取决于分布自由度v的值，自由度v的值越大，分布的尾部就越薄。由表1中自由度v的估计值可以看出，2个样本的自由度不相等, 但已知的二元分布一般都要求随机变量具有相同的边缘分布，所以很难应用现有的二元分布来拟合2个具有不同自由度的样本，因而不能简单的假定2个样本的联合分布服从一个特定的二元分布。

3 联合分布的拟合

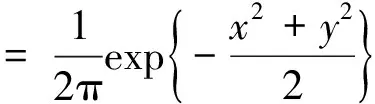
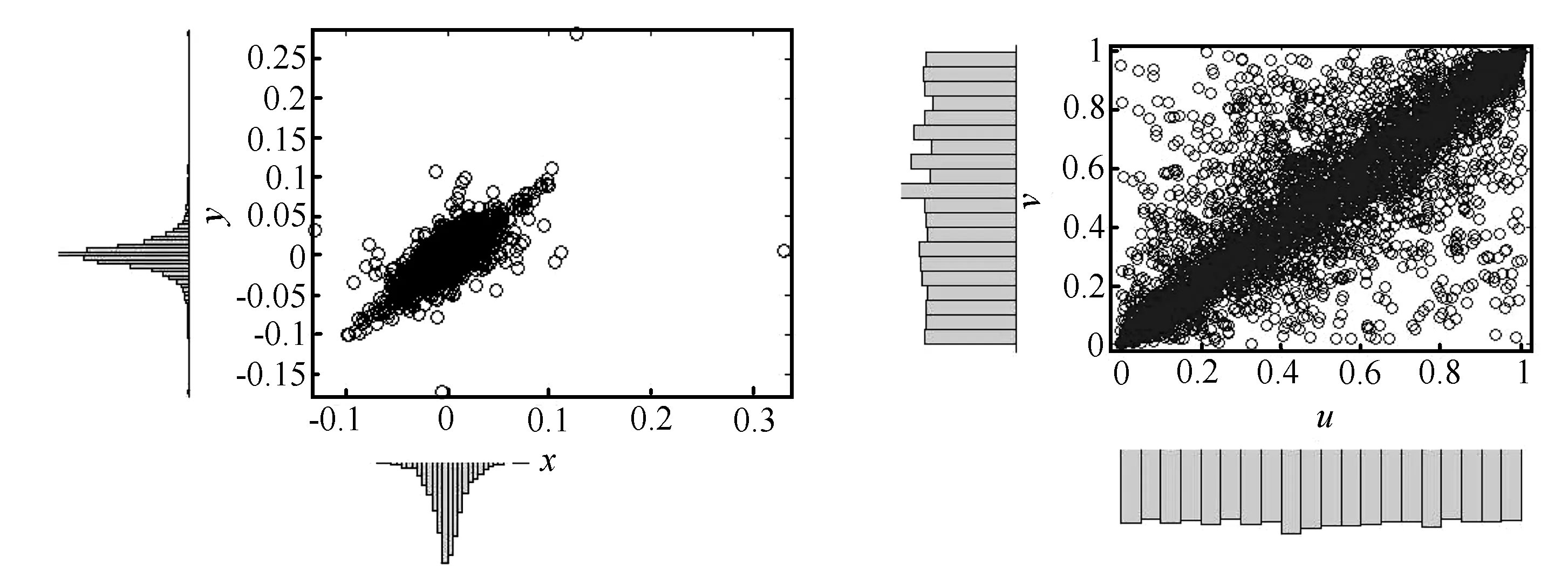
图2 联合分布散点图 图3 化为[0,1]区间上的联合分布散点图

利用Matlab的核密度估计工具箱做二维核密度估计。笔者选用二元Copula函数来作拟合，计算步骤如下：

步1 取上证综指的1990～2010年的日收益率样本为{Xi}，深证综指的1990～2010年的日收益率样本为{Yi},利用Matlab的scatterhist命令作出序列的散点图(见图2)。

步2 将步1得到的散点图进一步转化为[0，1]区间上的概率分布值(联合分布散点图见图3):

u = ksdensity(x,x,’function’,’cdf’);

v = ksdensity(y,y,’function’,’cdf’);

scatterhist(u,v)

xlabel(’u’)

ylabel(’v’)

步3 利用Matlab中copulafit和copulacdf命令分别得到将概率分布值用选定的Copula函数连接得到的Copula分布函数值和t-Copula函数的参数及Kendall秩相关系数τ值(0.8475)。程序代码片段如下：

[RHOHAT,nuhat,nuci] = copulafit(’t’,[u v])

R = copulastat(’t’,rho,NU)

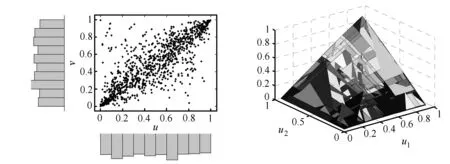
图4 t-Copula函数模拟得到的散点图 图5 t-Copula函数联接得到的分布函数图

步4 利用Matlab中copularnd命令得到联合分布的随机模拟数据(见图4)。程序代码片段如下：

t:r = copularnd(’t’,RHOHAT,nuhat,1000);

u1= r(:,1);

v1= r(:,2);

scatterhist(u1,v1)

xlabel(’u’)

ylabel(’v’)

x1=ksdensity(u,u1,’function’,’icdf’);

y1=ksdensity(v,v1,’function’,’icdf’);

scatterhist(x1,y1)

画出二元t-Copula函数连接得到的分布函数(见图5)。

4 结果与分析

由前面的计算结果可知，Kendall秩相关系数为0.8475.表明t-Copula拟合沪深两市的综合指数是合适的。

由二元t-Copula的Kendall秩相关系数公式和Spearman秩相关系数公式：

计算得出如下结果：Spearman秩相关系数ρ(0.8767)和Kendall秩相关系数τ(0.8475)的值均大于0.4，表明沪深综指之间存在很强的正向风险关联性，沪深收益率走势具有相同的方向[4]。ρ值显著大于0说明条件方差所表现出的风险立即在预期收益率中得到反映，表明了我国股市的风险传递机制在不断地发挥作用。同时，正的ρ值也意味着我国股市投资者的风险意识在不断增强，对风险的增加则要求有相应的风险补偿，股价波动不仅仅给投资者带来了风险，同时它所补偿的风险溢价是重要的收益来源。

[1]Hansen B E. Autoregressive conditional density estimation[J]. International Economic Review,1994,35(3):705-730.

[2]韦艳华，张世英，郭焱.金融市场相关程度与相关模式的研究[J].系统工程学报，2004，19(4):361-368.

[3] Nelsen R B.An Introduction to Copulas，Lectures Notes in Statistics[M].New York：Springer- Verlag Berlin Heidelberg，1998:49-158.

[4]Andersen T G, Bollerslev T, Francis X, et al. Modeling and forecasting realized volatility[J]. Econometrica,2003, 71(2):579-625.

2012-11-25

湖北省自然科学基金项目(2011CDB081)。

郑列(1963-)，男，硕士，教授，现主要从事应用数学方面的教学与研究工作。

O211.67

A

1673-1409(2013)04-0021-04

[编辑] 洪云飞