基于多岛遗传算法的深海复合材料悬链线立管优化设计

刘昊，杨和振

(1.上海交通大学船舶海洋与建筑工程学院海洋工程国家重点实验室，上海200240;2.上海打捞局，上海200090)

随着海洋油气开采走向深海，传统的钢立管难以满足设计要求.复合材料作为深海立管设计的替代材料具有很多优势，如:高比强度、高比刚度、腐蚀性能好，热导率低以及突出的阻尼特性和抗疲劳能力［1-2］.深海管线受到高温高压以及恶劣的海洋环境，复合材料的轻质量和良好的顺应能力可以减少顶部张力，确保安全性，满足设计需求，从而降低立管系统和平台建造的费用［3-4］.因此复合材料立管深水开发前景较好，但其在深海的应用面临众多的技术挑战.

悬链线立管顶端与触地区域均为设计中需要关注的重点区域［5］.随着设计水深增加，深海悬链线立管设计中需要关注的关键点是:1)连接平台的顶部应力接头是张力最大的区域［6］;2)触地区域与海床接触，曲率变化大，疲劳严重;3)立管安装时立管底部受到较高的静水外压，易发生屈曲破坏.

学者针对复合材料顶张力立管进行了研究，Meniconi等［7］考虑了百年环流环境载荷，强度校核表明复合材料接头可以满足设计要求，且重量不足钢制立管的一半;Wang等［8-9］对复合材料管进行了局部优化设计，前者使用的是三维实体单元有限元模型并对比了管体和内衬层使用不同材料的设计;后者使用的壳体单元建模，给出了不同设计变量时算法选择的建议.上述研究表明复合材料管的优化过程中，建模和算法选择没有统一标准，但设计中要考虑不同位置处的载荷，而关键截面载荷的提取往往需要依赖整体模型的分析，复合材料结构的优化往往遇到离散设计变量、目标函数多峰性等问题［10］，因此对于复合材料立管的优化设计，传统的单一局部优化模型对其不适用.本文提出一种将复合材料悬链线立管整体模型与局部模型结合分析的方法，并对壳体铺层进行优化设计.

1 复合材料力学及优化理论

1.1 复合材料层合壳面内工程弹性常数

刚性复合材料立管由一组铺层按一定厚度、铺角组合从而达到预期的刚度与强度，其假定各层之间完全粘结.在纤维增强复合材料中，每个片层的宏观力学表现可以视为均匀的各向异性材料.

复合材料层合结构广义应力应变关系表示为

式中:N、M为层合板横截面上的内力、内力矩，εm、k分别代表中面应变和面曲率，A、B、D分别为拉伸、拉弯耦合和弯曲刚度矩阵，式(1)中的系数通过计算得到:

等式两端同时除以壳体厚度h并作逆变换:

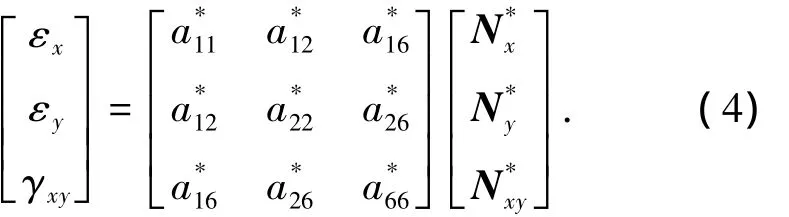
1.2 复合材料强度准则

对于各向同性材料仅需定义一个强度参数(屈服或断裂强度)，而对于正交各向异性材料，不同方向上具有不等的强度参数.层合板的失效有2种准则，即首层破坏失效(first ply failure，FPF)和极限失效(ultimate ply failure，ULF).FPF定义当任意一层单层板失效时为临界状态，而ULF是一种渐进失效分析，随着载荷增加失效的单层板的刚度会折减直至最后一层失效得到极限载荷.本文使用FPF作为定义失效的强度准则，失效准则使用了最大应力准则和Tsai-Wu准则.

1)最大应力准则(maximum stress theory，MST)

对于面内受力状态，通过坐标变换，求出材料主轴的应力 σ1、σ2、τ12.最大应力准则的判据为材料主轴方向的各应力分量必须小于各自的强度，即:

式中:上标T代表拉伸条件下的材料强度，C代表压缩时材料店强度，下标1、2分别代表材料1、2方向的主应力，S为剪切强度，该准则不考虑破坏模式之间的相互影响.

2)Tsai-Wu准则下材料满足强度条件的定义为

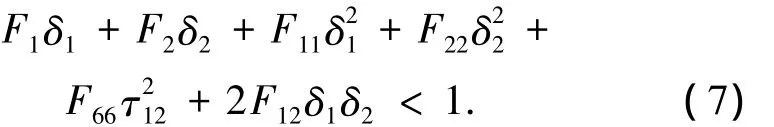
式中:

其中，Fi、Fij分别为2阶、4阶张量系数，安全因子是衡量应力分量与强度间的关系，对于最大应力准则的安全因子定义如下:

对于Tsai-Wu准则，安全因子的定义是用该值乘以应力分量恰好满足式(7)的等号条件.其数值等于一个二次方程的正根:

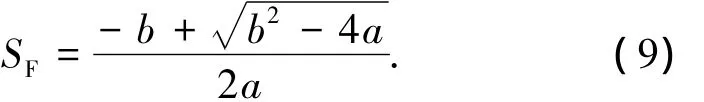
式中:

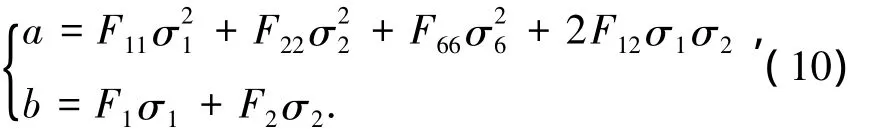
1.3 复合材料圆柱壳外压屈曲

圆柱壳体的屈曲载荷与管子的长度L，平均半径R，壁厚t，材料参数以及边界条件相关.Batdorf等［11-12］研究了各向同性圆柱壳稳定性，对几何参数与材料参数的影响做了深入分析.对于各向同性的圆柱长壳，弹性屈曲载荷可以表示为

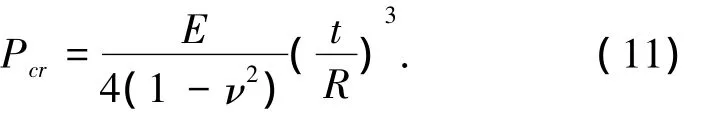
式中，ν为泊松比，对于短圆柱管由于端部约束的作用其临界压强会增加.由于几何缺陷的存在，会引起几何非线性并导致立管的承压能力下降.以设计角度来讲立管的坍塌压强由下式给出:

式中，kp代表几何缺陷的折减因子.Weingarten等［13］推荐短壳和长壳的 kp分别为 0.75 和 0.9.对于正交各向异性圆柱壳，Weingarten等［13］给出了如下的计算公式:

式中，A22、B22、D22是式(2)中的系数.

1.4 优化理论

深海复合材料立管优化设计问题包含复杂的约束条件，其目标函数具有多峰性、非线性、非连续、不可微;而设计变量也可能是包含连续、离散或分类值的混合变量，遗传算法可以有效解决上述问题.

多岛遗传算法(multi-island genetic algorithm，MIGA)［14］是建立在传统遗传算法上一种新型算法，继承了传统遗传算法中适应度、选择、交叉、变异等理念，又引入子种群(岛)的概念，如图1所示.MIGA将一个大的种群分成若干个子种群(岛)，在每个岛上运用传统的遗传算法进行子种群进化;MIGA算法每隔一定的代数，会按一定的比例选择各岛的个体，转移到其他岛上，完成种群间个体的交换，增加个体的多样性，这个操作称为迁移.各个岛屿的求解可能收敛于不同的局部最优解，结合迁移操作使得其保持了优化解的多样性，可以更好地在优化域中寻找全局最优解.

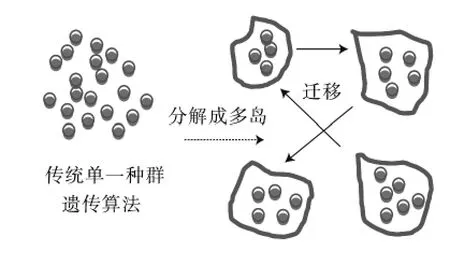
图1 多岛遗传算法中岛生成原理Fig.1 The principle of multi-island genetic algorithm

2 复合材料立管优化设计方法

传统的复合材料管设计中只是通过薄膜理论粗略估计轴向和环向需要的厚度.然后根据该模型参数校核其内压爆破压力下各层下的应力水平并计算其安全系数，最后调整厚度并重新分析直至满足安全要求并使总质量最优.

本文提出一种复合材料立管设计优化方法，将刚度等效、整体分析以及多载荷工况局部分析相结合进行立管整体的优化设计.如图2所示，在整体分析前，首先计算复合材料截面的等效刚度，然后用梁单元模型进行静力、动力分析.整体分析后，建立关键位置的细化局部三维模型，将整体分析中得到的截面内力作为边界条件加载到局部模型中并评估每层的应力或应变.该方法优点是可以将局部截面优化与整体分析结合起来，通过等效刚度计算和整体模型在极限载荷下的动力分析得到不同工况下的危险截面.而传统的设计方法整体分析与截面优化设计是孤立的.此外，通过这种方法可以直接找出哪些约束直接影响设计结果，使得优化的针对性更强，分析流程如图3所示.

图2 整体模型与局部模型分析关系Fig.2 The relationship between global and local analysis

图3复合材料悬链线立管优化设计流程Fig.3 The design flow of the composite catenary riser

3 复合材料悬链线立管优化算例

设计变量是每层的厚度和铺角，铺层的数量和材料定义为已知参数，目标是最小化立管的成本，即复合材料使用量.优化模型中强度和稳定性约束被包含在多个载荷工况下(如安装、工作).

算例中的数据如表1所示，复合材料立管内衬层使用钢，复合材料为碳纤维环氧基复合材料，材料参数如表2所示.

初始设计选用正交铺设方式，铺角关于中线面对 称，为 (90°/0°/90°/0°/90°)s，内 衬 层 厚 度为 mm，复合材料各层厚度均为2 mm.

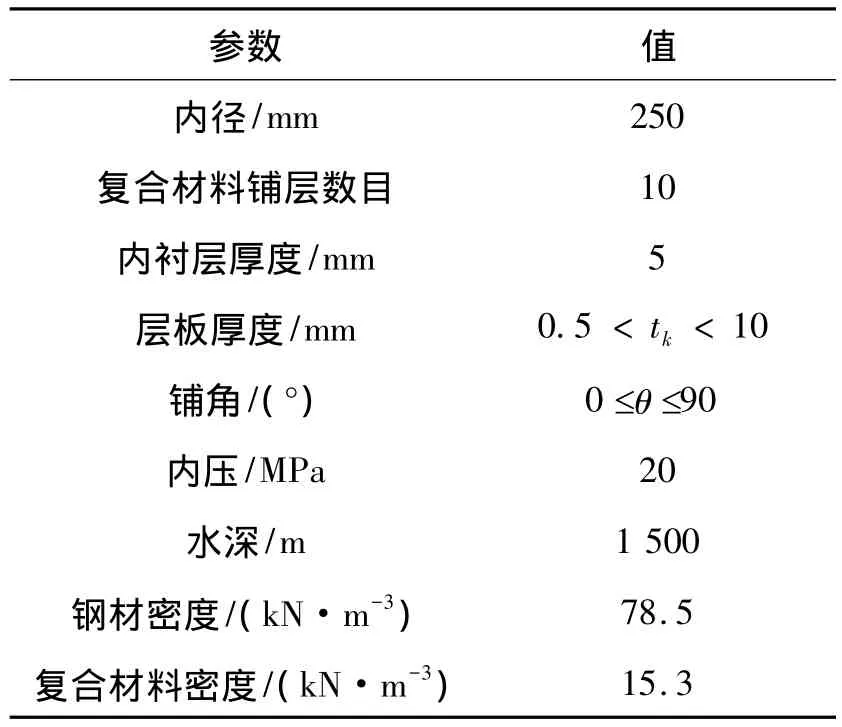
表1 复合材料立管设计参数Table 1 Parametric research for the example

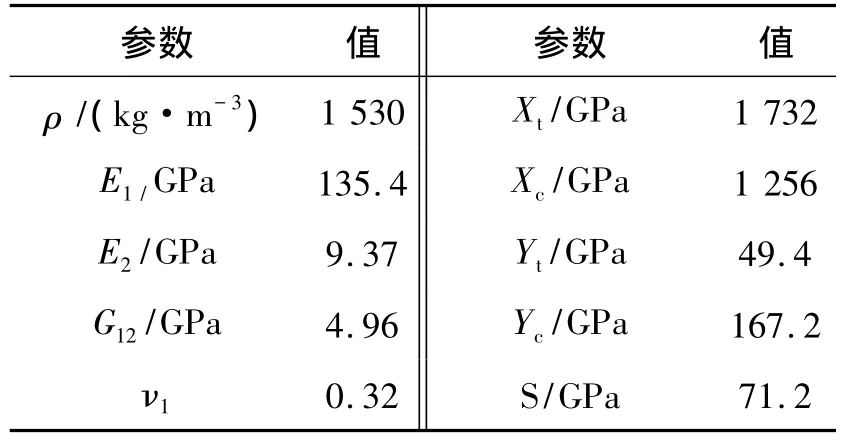
表2 AS4-Epoxy材料属性Table 2 The material property of AS4-Epoxy

3.1 极限载荷下复合材料立管整体分析

悬链线立管整体模型可以视为等截面形式的连接平台与井口的等效结构.计算复合材料梁的截面力学参数需要通过经典层合理论，根据初始设计参数可以得到其等效截面力学参数，复合材料李冠的轴向等效弹性模量75.3 GPa，环向等效弹性模量102 GPa，等 效 剪 切 模 量 5.76 GPa，等 效 泊 松比0.072.为了局部模型提供准确的设计载荷条件，需要将环境载荷(波浪、流)加载到整体模型中.其相关参数如表3、4.

表3 波浪参数Table 3 Wave parameters

表4 百年一遇流载荷Table 4 100-year loop current data

图4出了海洋环境下沿立管管长的轴向张力、弯矩的分布.图中可以看出立管顶部受重力引起的张力最大，弯矩在顶部和触地区域均较高，尤其是触地区域，这主要是由接触和几何非线性引起的，因此这2个区域是分析中的关键截面.从整体分析中可以看出顶部悬挂区承受较高的拉力，而触地点区域弯矩较大.因此出于安全因素的考虑，在立管的优化设计中，需要对这2个区域同时考虑.

图4 复合材料悬链线立管张力和弯矩Fig.4 Axial tension ＆ bending moment of the catenary composite riser

3.2 关键截面的局部分析

本文选择了关键截面的3种危险工况作为局部分析模型:1)百年环流海况下顶部悬挂区在立管内压时的情况(工况A);2)底部触地区域在内压及百年环流载荷作用下的情况(工况B);3)底部空管形态下(内压为0)外压屈曲稳定性的约束(工况C).工况A、B是强度分析，工况C属于稳定性分析，均可通过有限元进行建模分析.

将危险工况下整体分析中的关键截面响应提取并以边界条件和载荷的形式加载到局部模型中，就可以得到各层的应力分布，由于各层内应力分布并不连续，因此需要将各层的应力分别提取出来并带入合适的强度准则中进行校核.

局部模型长度取0.5 m，对于厚壳结构，使用三维实体单元得到的应力结果更加精确，沿壁厚划分3层单元，由内至外分别为内衬层、内部5层复合材料以及对称的外5层复合材料，有限元模型见图5.

图6为复合材料立管初始设计参数在工况A下各复合材料层的安全系数，内衬层的Von Mises应力为224 MPa.图中可以看出纤维沿轴向铺设(0°铺层)的安全系数较低，同时Tsai-Wu准则得到的安全系数较最大应力准则要高.

用有限元进行立管外压屈曲分析时，模型长度选择对得到的屈曲载荷影响很大.通过对长度进行参数分析，得到当立管模型长度超过某一值时，屈曲载荷将趋于某一固定值，本文得到该模型长度约为2.5 m，图7为复合材料立管一阶外压屈曲模式，初始设计得到的屈曲载荷为139.5 MPa.经过上述分析可以看出初始设计的安全裕度较大，在安全情况满足的情况下不经济，因此需要对其进行成本优化.

图5 三维有限元模型Fig.5 3D model of finite element analysis

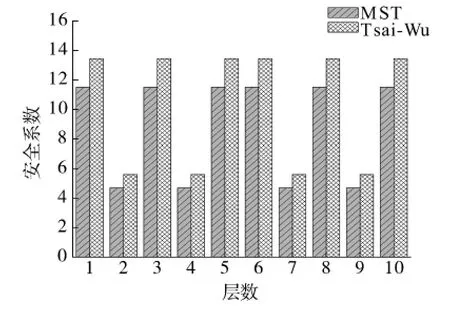
图6 顶部区域各层工况A安全系数Fig.6 The safety factor of each layer at the hang-off(case A)

图7 立管一阶外压屈曲模式Fig.7 The First buckling mode of riser

3.3 复合材料立管设计参数优化研究

从前面的分析可以得出初始设计是偏于保守的，由于复合材料的裁剪性能良好，因此可以结合优化算法设计出更加经济的方案，充分发挥材料性能.基于整体分析得到的关键截面载荷的提取，以局部强度分析和稳定性为约束条件，对复合材料悬链线立管进行减重优化.

问题给出的输入参数包括材料属性、立管内径Ri，内衬层厚度tliner，复合材料铺层数n，安全系数以实际设计规范为参考标准［13］.本文使用表1给出的设计参数:

设计变量:

1)复合材料铺层厚度 ti(i=1，2，3，4，5)，为离散型变量，取值为 0.5、1、1.5、2 mm

2)复合材料铺层纤维铺设方向 θi(i=1，2，3，4，5)，为离散型变量，取值为0°、±90°、±45°

约束条件为:

1)内衬层满足强度约束，使用屈服强度为710 MPa的钢材，应力安全系数大于1.5.

2)复合材料铺层满足强度约束，分别使用最大应力准则和Tsai-Wu准则，应力安全系数大于3.0.

3)立管底部满足外压屈曲稳定性条件，屈曲安全系数大于3.0(即1 500 m水深屈曲载荷 Pcr＞45.2 MPa).

目标函数:单位长度立管的质量最小，即 min W(R，tliner，ti).具体优化模型如下:

优化中使用近似模型技术以提高优化效率，其原理是将约束、目标函数与变量间的隐式关系用显式的函数逼近，优化算法使用适用于多峰探索的多岛遗传算法，算法参数设置岛数10，进化代数10，种群数 10，交叉概率 1，迁移率 0.5，变异率0.01.复合材料强度首先选择最大应力准则，优化中重量迭代如图8所示，优化后复合材料立管铺层厚度如表5所示，铺角为(90°/45°/0°/90°/－45°)s铺层厚度减少 45%，立管干重减轻21.6%，在满足安全系数的条件下经济成本大为降低，其中内衬层强度为临界约束.

图8 复合材料立管单位质量优化迭代图Fig.8 Iteration of the weight of composite catenary riser

表5 优化前后参数比较Table 5 Comparison between initial and optimized parameters

最后选择Tsai-Wu准则作为强度理论进行优化，优化厚的各层铺层厚度为 2、0.5、0.5、2、0.5 mm，铺角为(90°/45°/0°/90°/－45°)s.通过对比 2种强度准则下的优化结果，两者优化后的铺角与总厚度一致，各层厚度略有差异.

4 结束语

复合材料立管由于其质量轻，比强度、比刚度高等优势，在深海石油开采中的应用前景较好.然而其较钢制立管设计更为复杂.本文提出了一种深海复合材料悬链线立管铺层优化设计方法，运用了刚度等效－整体－局部联合分析方法.由于铺层设计中含有大量的参数，并且其对性能的影响也不是单调的，因此采用优化设计的方法对复合材料立管的铺层进行设计，优化算法使用多峰搜索能力较强的多岛遗传算法.通过算例分析验证了这种分析方法的有效性，并且基于规范设计对复合材料部分进行减重优化，在强度和稳定性满足要求的情况下质量减轻21.6%，说明本文提出的优化方法可以较好的改进复合材料立管的设计，对工程实际有一定的借鉴价值.

［1］PRICE JC.The"state of the art"in composite material development and applications for the oil and gas industry［C］//Proceedings of the Twelfth(2002)International Offshore and Polar Engineering Conference.Kitakyushu，Japan，2002:125-131.

［2］ODRU P，POIRETTE Y，STASSEN Y，et al.Composite riser and export line systems for deep offshore applications［C］//22nd International Conference on Offshore Mechanics and Arctic Engineering;Materials Technology Ocean Engineering Polar and Arctic Sciences and Technology Workshops.Cancun，Mexico，2003:147-156.

［3］OCHOA OO，SALAMA M M.Offshore composites:transition barriers to an enabling technology［J］.Composites Science and Technology，2005，65(15/16):2588-2596.

［4］BEYLE A，GUSTAFSON C，KULAKOV V，et al.Composite risers for deep-water offshore technology:problems and prospects.1.Metal-composite riser［J］.Mechanics of Composite Materials，1997，33(5):403-414.

［5］YANG H Z，LIH J.Sensitivity analysis of fatigue life prediction for deep water steel lazy wave catenary risers［J］.Science China Technological Sciences，2011，54(7):1881-1887.

［6］郑文青，杨和振.深海钢悬链立管应力接头的多轴疲劳分析［J］.哈尔滨工程大学学报，2011，32(11):1422-1427.ZHENG Wenqing，YANG Hezhen.Multiaxial fatigue analysis of the stress joint for a deepwater steel catenary riser［J］.Journal of Harbin Engineering University，2011，32(11):1422-1427.

［7］MENICONI L，REID S，SODEN P.Preliminary design of composite riser stress joints［J］.Composites Part A:Applied Science and Manufacturing，2001，32(5):597-605.

［8］WANG CG，SHANKAR K，MOROZOV E V.Tailoring of composite reinforcements for weight reduction of offshore production risers［J］.Applied Mechanics and Materials，2011，66(1):1416-1421.

［9］HARTE A M，MCNAMARA JF，RODDY I.Evaluation of optimisation techniques in the design of composite pipelines［J］.Journal of Materials Processing Technology，2001，118(1):478-484.

［10］王宏伟，任慧龙，戴仰山.基于遗传算法的油轮中剖面横构件优化设计［J］.哈尔滨工程大学学报，2003，24(1):14-16.WANG Hongwei，REN Huilong，DAIYangshan.Optimum design of midship sectional transverse members based on genetic algorithm［J］.Journal of Harbin Engineering University，2003，24(1):14-16.

［11］BATDORF SB.A simplified method of elastic-stability analysis for thin cylindrical shells.2-Modified equilibrium equation.NACA874［R］.Washington DC，1947.

［12］BRUSH D O，ALMROTH B O.Buckling of bars，plates，and shells［M］.New York:McGraw-Hill，1975:200-216.

［13］WEINGARTEN V，SEIDE P，PETERSON J.Buckling of thin-walled circular cylinders.NASA SP 8007［S］.Washington DC:Space Vehicle Design Criteria(Structures)，1968:152-167.

［14］TANESE R.Distributed genetic algorithms for function optimization［D］.Ann Arbor:University ofMichigan，1989:70-78.