隐含变向时域有限差分方法的MPI实现
李太全,陈 威 (长江大学物理科学与技术学院,湖北 荆州 434023)
隐含变向时域有限差分方法的MPI实现
李太全,陈 威 (长江大学物理科学与技术学院,湖北 荆州 434023)
在MPI环境中,研究了适合于隐含变向时域有限差分算法(ADI-FDTD)的虚拟拓扑和节点间的数据通信。将并行对角占优算法(PDD)应用于ADI-FDTD,极大地减少了并行节点间的数据通信。进一步分析数据通信的传输速率,提出了数据成批传送方案,实现了ADI-FDTD的高效率并行计算。
MPI;隐含变向时域有限差分算法;三对角方程组;并行对角占优算法
时域有限差分算法(FDTD)[1]在电磁场辐射和散射、微波电路以及电磁兼容等领域获得了非常成功的应用。然而,较长的计算时间和较大的存储空间是FDTD在PC系统上求解复杂电磁场问题的瓶颈。 解决这一问题的有效方法之一是采用并行FDTD方法[2-3]实现FDTD的分布运算。随着计算机网络的迅速发展,基于消息传递接口(MPI)[4]的编程环境被广泛采用,是目前最重要的并行编程工具,该系统具有移植性好、功能强大、效率高等诸多优点,已经成为国际上一种并行程序标准,被越来越多的硬件生产厂商和计算机用户所接受。
显式FDTD的时间步长受Courant条件限制,在精细结构的电磁分析中,由于空间步长远小于电磁波波长,其计算效率显著降低。隐含变向时域有限差分算法(ADI-FDTD)[5-6]的提出,打破Courant条件限制,计算效率得到了明显提高。然而,ADI-FDTD算法需要求解一组三对角方程,这组方程导致了并行ADI-FDTD方法复杂化。笔者将应用三对角矩阵并行算法,实现ADI-FDTD的并行计算。
1 子区域划分与虚拟拓扑
将整个FDTD 计算区域划分为若干个子区域,每个进程(或线程)计算其中的一个子区域,各个进程之间通过通信传递交界面上的电磁场量,以实现FDTD 中电磁场量的递推。子区域的分解方法应根据计算区域的尺度,在权衡运算开销和通信开销的前提下选择划分方案。一般采用图1所示的方法[2],将计算区域沿着3个方向分解为子区域。MPI提供了迪卡儿拓扑和图拓扑,根据上述的子区域划分,每个子区域对应一个进程,而每个进程对应拓扑中的一个节点,所以,应选择笛卡儿拓扑。
2 ADI-FDTD的三对角方程组与PDD算法
隐含变向时域有限差分算法将一个时间步的电磁场量递推分为2个亚时间步[4],在每个亚时间步的递推运算中,6个电磁场分量有3个需要求解三对角方程,如果在第一个亚时间步选定Ex、Ey、Ez应用方程组求解,则Hx、Hy、Hz可以直接计算。以Ex为例,对应的三对角方程可表示为:
(1)
式中,α、β、γ、p、q是与空间步长、时间步长和介质的电磁特性相关的系数。
第2个亚时间步计算式与式(1)类似。关于方程组(1)的求解,由于在z轴方向上Ex相互牵连,需要将图1中沿z轴位于同一直线的子区域合并考虑,如图2所示。

图1 子区域分解 图2 求解Ex相关联的子区域
求解方程(1)可采用并行对角占优算法(PDD)[7]。对确定的i、j,方程(1)可表示如下:
(2)

将矩阵A分解为:
V=[αmum,γm-1um-1,…,αm(Np-1)um(Np-1),γm(Np-1)um(Np-1)-1]
U=[um-1,um,…,um(Np-1)-1,um(Np-1)]
式中,A(p)为m×m阶三对角矩阵,对应图2中的一个子区域;(p)表示子区域编号;um为Nz个元素的列向量,且除第n元素为1外,其他元素均为0。
式(2)的解可以写成:
(3)
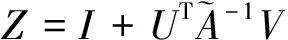
(4)
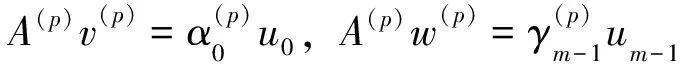
(5)
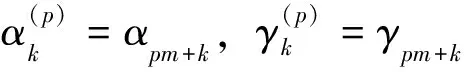
αk=-Δt/(μ(i+0.5,j,k-0.5)Δz2)
γk=-Δt(μ(i+0.5,j,k+0.5)Δz2)
(6)

1)确定当前节点p对应子区域中网格i、j对应的A(p)和d(p);
移动网络的网络节点是人,而不是网页,也就是说人人都是数据的产生着和携带者,无论是微信、照片、微博等任何网络相联系的,都已成为数据的产生者。所涉及到的资料总量是目前任何一个软件都不可能接受、管理、处理、总结的。有国外机构预测,全球的数据量将在2020年扩大到目前的五十倍,这样就意味着大数据时代的容量将会更多、更大、更难处理。
2)求解方程组:
(7)
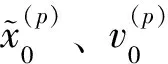
4)求解方程组:
(8)
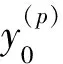
(9)

tC=2NxNytα+12NxNytβ
(10)
式中,tα为通信响应时间;tβ为一字节数据的传输时间(浮点数为4字节单精度实数)。对试验网络测试,tα=26.3μs,tβ=0.0875μs。由于tα≫tβ,将数据成批传送会大大提高通信效率。为此,采用如下步骤求解方程(1):
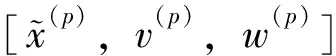
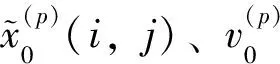
3)对i、j循环,求解方程(8),并存储y0,y1;
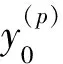
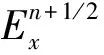
这样, 原来的2×Ny×Ny次数据通信减少为2次,此时通信时间开销为tC=2tα+12NxNytβ。
3 效率分析与数值试验
设子区域内FDTD网格数为Nx×Ny×Nz,在一次循环迭代中,运算开销约为6(te+th)NxNyNz,其中te、th分别为一个电场、磁场计算所需时间,通信开销约为18tα+28tβ(NxNy+NyNz+NzNy),算法的效率可以表示为:
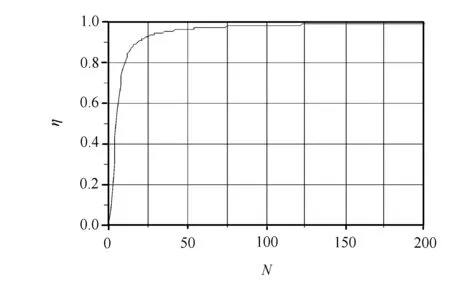
图3 在Nx=Ny=Nz=N时,效率与网格数N的关系
可见,当子区域的网格数Nx=Ny=Nz时,算法效率最高。
由个人计算机组成10个节点的集群系统,每个节点的CPU主频2GHz,内存1024MHz,100/1000M网卡,100M交换机。在该系统中测得,te=0.583μs,th=0.104μs,tα=26.3μs,tβ=0.0875μs。在该系统中,取Nx=Ny=Nz=N时,算法的效率如图3所示,在N>25时,算法已具有较高的效率。进一步检验算法的效率,笔者计算了如图4所示的环形天线。在相对介电常数为εr=4.5、边长为1000m、厚为h=50m的正方形基板上,有一个线宽b=12m、边长a=500m的正方形环带状线天线,激励点位于底边的中点E。激励源输出阻抗Z=100Ω,输出电压v(t)=exp(-4π(t-t0)2/τ2),其中τ=100ps。将整个空间划分为Nx×Ny×Nz=300×40×300网格,且Δx=Δy=4m,Δz=10m。取时间步长Δt=2×Δx/c,将空间在XY面等分为2、4、9个子区域。对该系统进行200时间步迭代,运算时间如表1所示。
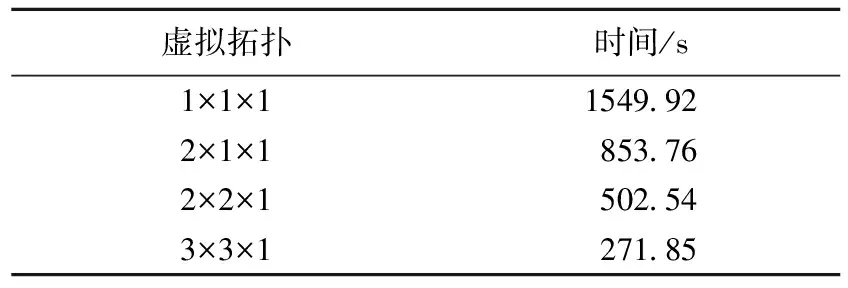
表1 不同区域划分的运算时间比较
图5是在上述4种情况下,分别得到天线输入口的S11,4种情况下的良好一致性说明了上述算法的正确性。
4 结 语
采用MPI编程环境,实现了ADI-FDTD的并行计算。将PDD算法应用于并行ADI-FDTD,极大地减少了节点间的数据传送量,减小了通信开销。并采用交换信息的成批传送,减少通信次数,虽然需要额外内存开销暂存临时数据,但可以显著提高了计算效率。
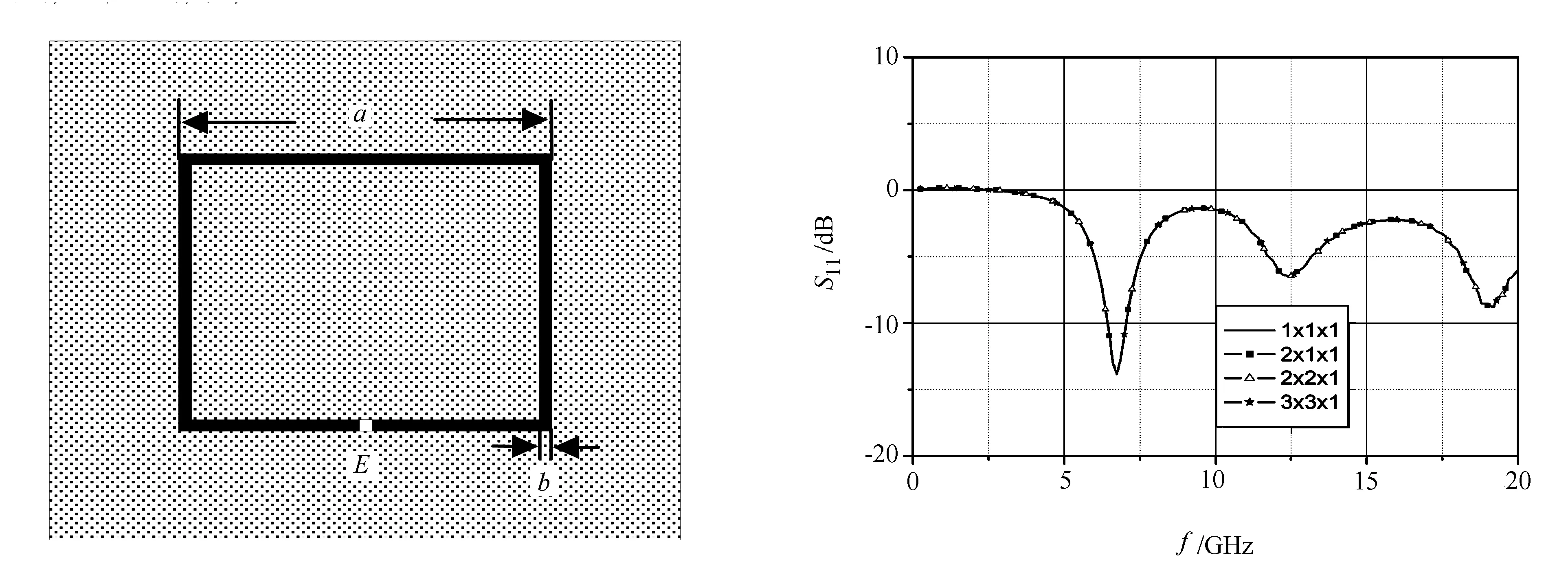
图4 环形天线结构 图5 4种情况下天线的S11
[1]葛德彪, 闫玉波.电磁波时域有限差分方法[M].西安:西安电子科技大学出版社, 2002.
[2] 张玉, 李斌, 梁昌洪. PC集群系统中MPI并行FDTD 性能研究[J].电子学报, 2005, 33(9):1694-1697.
[3] 杨利霞, 葛德彪, 郑奎松,等.电各向异性介质FDTD 并行算法的研究[J].电波科学学报, 2006, 21(1):43-48.
[4] 都志辉.高性能计算并行编程技术[M].北京:清华大学出版社, 2001.
[5] Namiki T.3-D ADI-FDTD Method Unconditionally Stable Time-Domain Algorithm for Solving Full Vector Maxwells Equations[J].IEEE Transactions on Microwave Theory and Techniques, 2000, 48(10): 1743-1747.
[6] Namiki T.A New FDTD Algorithm Based on Alternating-Direction Implicit Method[J].IEEE Trans- actions on Microwave Theory and Techniques, 1999, 47(10): 2003-2007.
[7] Sun X H, Zhang H, Ni L.Efficient Tri- diagonal Solvers on Multicomputers[J].IEEE Trans-actions on Computers, 1992, 41(3): 286-296.
2012-10-15
国家自然科学基金项目(41140034)。
李太全(1961-),男,博士,副教授,现主要从事电子技术方面的教学与研究工作。
TN911.2
A
1673-1409(2013)01-0006-04
[编辑] 洪云飞

