地震学百科知识(二)----震源物理(上)*

许忠淮 李世愚

(中国地震局地球物理研究所, 北京100081)

1 震源机制 (focal mechanism)

震源机制是指引起地震的震源处地球介质的运动或变形方式。 通常所说的震源机制是指天然构造地震发生的机制。

20世纪初叶， 人们根据地质和地形变的观测结果提出了构造地震的断层成因说。 至20世纪中叶， 对地震辐射的地震波的观测发现， 初始P波的初动方向、 振幅大小和初始S波的偏振方向和振幅大小等， 在震源周围均呈现出4象限分布的特征。 震源处分隔4象限的相互垂直的两个平面就是辐射P波振幅为零的节平面， 但P波节平面处恰是S波振幅大的方向。 接着， 又发现辐射面波的强度也存在4象限分布特征。

为解释这些观测结果， 有人用震源处突然释放了一个集中双力偶力系的震源模型， 称为双力偶点源模型(图1a)， 来解释地震波的辐射图像。 另外， 也有人用地震断层发生纯剪切错动的模型(图1b)来解释震源辐射地震波的特征， 震源处断层面延伸的平面就是辐射P波的一个节平面， 震源处另一个垂直于断层面的平面(称为辅助面)也是P波的节平面。 1958年加拿大Steketee[1]提出了震源的三维弹性位错理论， 由此理论证明，对于辐射的远场地震波来说， 小平面位错震源模型与双力偶点源模型是完全等价的。 于是， 震源的双力偶点源模型成了描述构造地震(特别是中小地震)震源机制的常用模型， 由地震波观测求出的该模型的参数解称为地震的震源机制解(focal mechanism solution)， 也有人称为地震的断层面解(fault plane solution)。

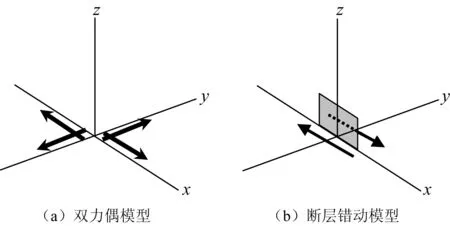
图1 地震的点源模型

根据弹性力学理论， 由双力偶震源模型计算出来的震源辐射的初始P波位移和初始S波位移矢量在震源球面上的分布表示于图2。 震源球面是个包住震源的假想球面， 该面上只出现由震源引起的连续弹性位移。 图2说明， 初始P波和初始S波位移都呈4象限分布， P波有两个位移为零的节平面， 二者相互正交， 其中的一个可能与断层面延伸方向一致。 在二节面的交线方向上， 震源既不辐射P波， 也不辐射S波。 震源辐射的S波位移方向都与震源球面相切， 球面上向着震源的P波位移最强点(P轴)正好是S波矢量在球面上发散的中心点(该点S波位移为零)， 而离开震源的P波位移最强点(T轴)则是会聚S波的零中心点。 震源的这些辐射特征已被大量的地震波观测所证实。

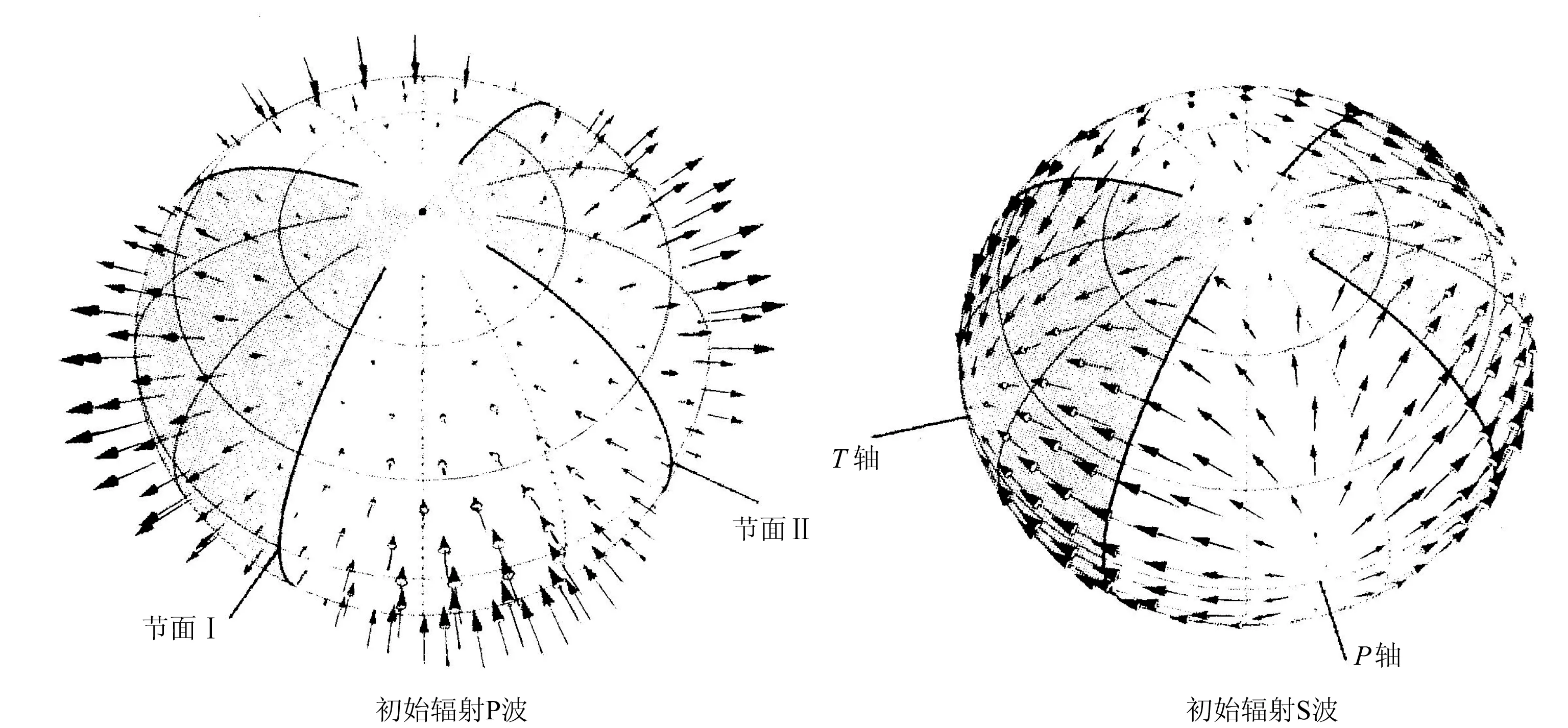
图2 双力偶点源发出的初始P波和初始S波位移矢量在震源球面上的分布[2]

上述双力偶模型或断层错动模型都是将震源看成是 “点源” 的模型。 在观测点与震源的距离(震源距)远大于震源本身的尺度、 且震源所辐射地震波的波长比震源距小得多的条件下， 可将震源近似看成是点源。 20世纪70年代前， 人们一般是按双力偶点源模型(或平面断层的纯剪切错动)来认识构造地震的震源机制的。 后来研究人员注意到， 实际地震的震源过程可能比平面断层的纯剪切错动更复杂， 于是进一步发展了描述震源机制的地震矩张量模型。

2 地震断层 (earthquake fault)

作为近似模型， 地震的发生常用平面断层突然发生的剪切错动来描述， 并称之为地震断层。 通常用断层的走向φS、 倾角δ和滑动角λ三个参数来描述地震断层(图3a)。 按目前国际上常用的描述方法， 这些参数的定义是：

走向φS： 断层面与水平面交线的方向； 但此交线有两个方向， 为唯一确定起见， 按以下原则确定其中之一为断层的走向： 人沿走向看去， 断层上盘在右。 走向用从正北顺时针量至走向方向的角度φS来表示， 0°≤φS< 360°。

倾角δ： 断层面与水平面的夹角； 0°<δ≤90°。

滑动角λ： 在断层面上量度， 从走向方向逆时针量至滑动方向的角度为正， 顺时针量至滑动方向的角度为负。 滑动方向指断层上盘相对于下盘的运动方向。 -180°<λ≤180°。

走向φS和倾角δ是断层的几何参数， 两者规定了断层的产状。 滑动角λ是断层的运动参数， 由这一参数的具体数值， 即可描述断层的各种运动类型(图3b)。 例如：λ≈0°表示左旋走滑断层(断层水平错动， 人在断层任一侧面对断层， 另一侧向左)；λ≈±180°表示右旋走滑断层(断层水平错动， 人在断层任一侧面对断层， 另一侧向右)；λ≈+90°表示逆断层， 上盘向上运动；λ≈-90°表示正断层， 上盘向下运动。

逆断层和正断层又统称倾滑断层， 因为断层两盘都是沿断层面的倾斜方向发生相对滑动的。 有人用断层的倾向代替走向， 倾向指下盘断层面向上的法线之水平投影的方向， 倾向恒等于走向加90°。 在地震震源研究中不常用倾向描述地震断层。

图3 描述平面地震断层的参数(a)及断层类型区分(b)

3 震源机制参数(focal mechanism parameters)

如果知道了地震是哪个断层的错动， 就可用断层的走向φS、 倾角δ和滑动角λ这3个参数来描述该地震的震源机制。 但是， 用地震波分析方法一般不能很快确定出发生地震的断层面， 对于中小地震， 更难以确定断层面； 因而地震的震源机制解通常给出的是震源处辐射P波的两个节平面， 分别称为节面Ⅰ和节面Ⅱ(图4a)， 其中之一可能是实际断层面。 震源机制解分别给出二节面在地平坐标(图3a， 图4b)下表示的走向、 倾角和滑动角(表1)。

两个相互垂直的节平面将震源区分为4象限， 地震断层错动特点决定了其中有两个顶对的象限初始是向外辐射挤压P波， 另两个象限是辐射拉伸P波(初始拉向震源， 图2)。 二节面交线方向称B轴(或N轴， 图4a)。 在辐射挤压波的二象限内， 在垂直于B轴的x-y平面内平分二节面夹角的方向是辐射挤压波最强的方向， 这两个方向称为震源机制解的T轴(图4a)； 而在辐射拉伸波的二象限内， 平分二节面夹角的方向称为P轴。P、T、B轴不是方向单一的矢量， 它们都可取两个互为相反的方向， 表达震源机制解参数时， 通常总是给出P、T、B轴的下倾方向的方位角和倾角(图4b， 表1)。

作为例子， 表1给出了一个地震的震源机制参数， 表旁绘出了该震源机制的下半震源球等面积投影图。 用双力偶震源模型描述震源时， 通常如表1所示可给出12个参数； 但独立参数只有3个， 根据这12个参数中的任意3个可计算出其余9个参数。 实用中有时使用节面Ⅰ或节面Ⅱ的3个参数作为独立参数。

表1 2008年5月12日汶川8.1级地震的震源机制参数(哈佛大学解)

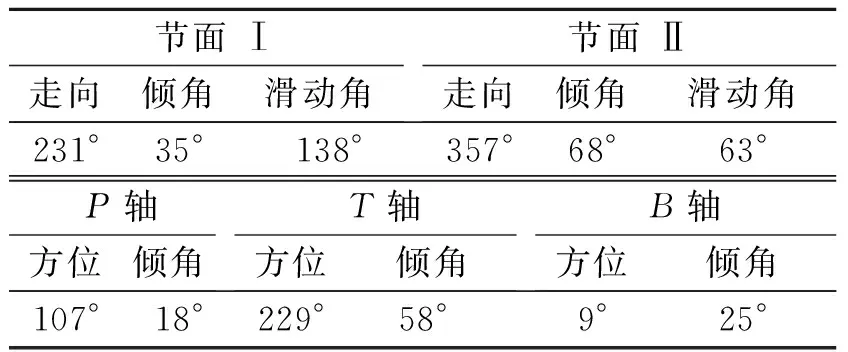
节面 Ⅰ走向 倾角 滑动角 节面 Ⅱ走向 倾角 滑动角 231° 35° 138° 357° 68° 63°P轴方位倾角T轴方位倾角B轴方位倾角 107° 18° 229° 58° 9° 25°

4 震源机制投影图 (focal mechanism projection)

地震的震源机制解常用平面的立体投影图来表示， 这需要借助于某种将球面上的点与平面上的点一一对应起来的投影法。 常用的有乌尔夫网和施密特网投影法。 二方法的投影平面通常取过震源球心的水平大圆面(图5a)(也可以取过球心的其他某个大圆面)， 投影点为与水平大圆面相对的极点。 震源机制解通常用下半震源球面的投影， 这时投影点为震源球面的上极点Z。

图5 乌尔夫网投影法的图示

要投影上半震源球面上的某点R(图5a)时， 可将半径OR向相反方向延伸至下半震源球面上R的对蹠点后， 再找对蹠点在投影网上的位置。

乌尔夫网投影是一种等角投影， 球面上曲线的交角投影到平面上后保持角度不变。 施密特网投影又称等面积投影， 球面上面积相等的区域投影到平面上后仍保持面积相等。

用逐点投影的方法， 可得到震源球面上任意曲线的投影。 现说明如何在投影网上表示震源机制解的节平面和力轴。 如图6a所示， 过震源球心的直立大圆面ABC在网上的投影是过网心的直线A′B′C′。 与大圆面ABC走向(φs)相同、 但倾斜的大圆面ADC在网上的投影是A′D′C′。 网上D′G线段的长短表示倾角δ的大小。 倾角愈大， 投影曲线愈接近网心； 倾角愈小， 曲线愈靠近网边。 图6b表示， 由任一力轴的方位角AZ和力轴的下倾角PL， 可得力轴在下半震源球面上的出头点Q在投影网上的投影点Q′。

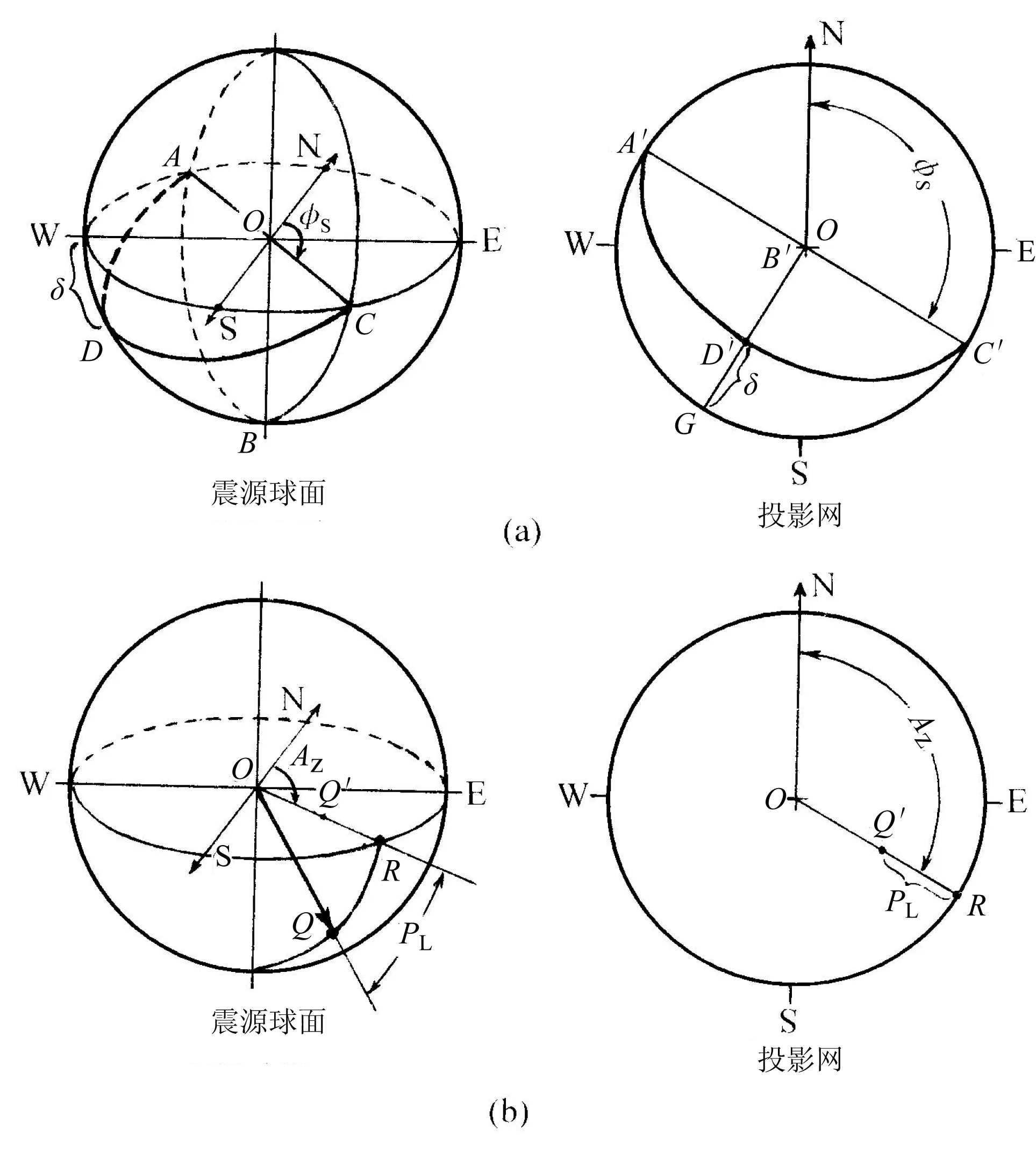
图6 (a) 节平面在投影网上的表示; (b) 力轴在投影网上的表示

图7给出几种典型震源机制投影图及其相应的可能断层产状和错动特征。

5 双力偶震源模型 (double couple source model)

描述平面断层纯剪切错动的震源可以用双力偶震源模型(图8a)， 弹性理论已证明， 在产生地震波或引起震源外围介质的形变方面， 双力偶力系与双偶极力系的作用(图8b)是等价的。 这两种力系都是合力与合力矩均为零的力系作用， 符合震源是弹性体中内力作用结果的实际情况； 但这种力系可使震源体发生变形， 如果震前有一个包住震源区的球形体， 震后则变为椭球体(图8c)， 震源向外扩张最强的方向正好是震源辐射初始P波最强的方向， 即震源机制解的T轴方向(图4a， 表1)， 向内收缩最强的方向正好是P轴方向。 注意， 对双力偶模型， 与力偶所躺平面(图8，x-y平面)垂直的z轴方向是没有力作用的， 震后椭球体的该轴方向不发生形变。

图7震源机制投影图及相应的断层错动类型。左图用了下半震源球等面积投影，黑区表示震源初始向外挤压的象限，白区表示震源初始向内收缩的象限。中图和右图的断层错动分别与震源机制的两个不同的节面相对应[2]

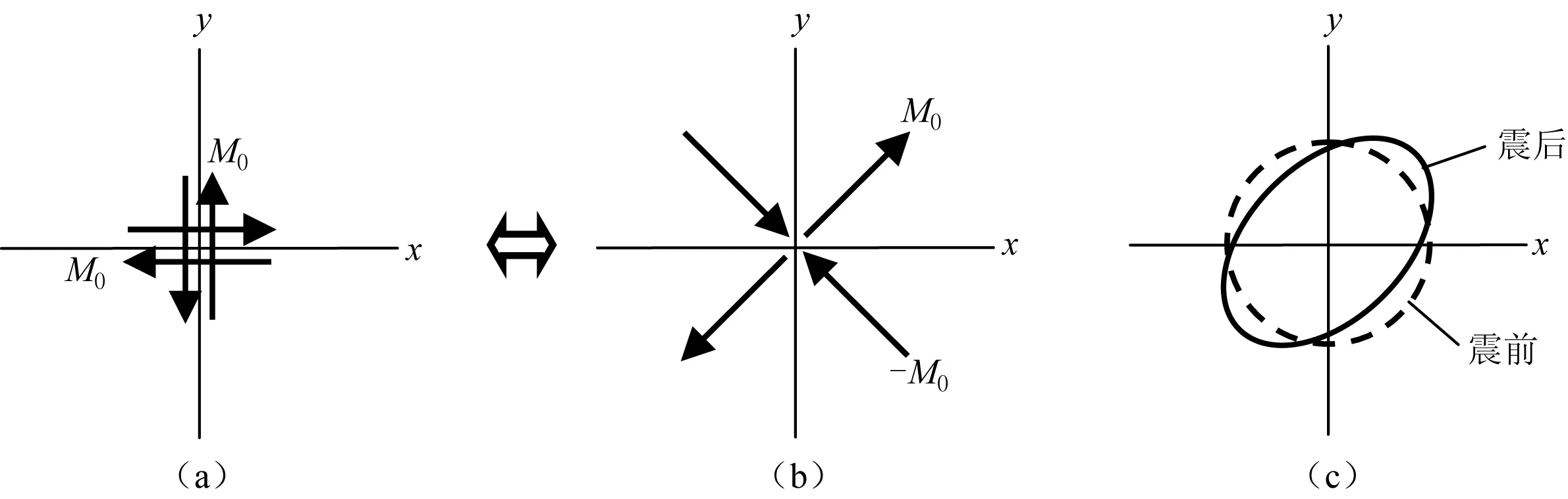
图8 作为震源模型的双力偶力系(a)与双偶极力系(b)的等价性和震源区的变形(c)

由于双力偶点源辐射地震波的总体强度是受一个力偶矩(或一个偶极矩)的大小控制的， 即若这个力偶矩值增大一倍， 向各个方向辐射的地震波的振幅都会增强一倍， 因而这个力偶矩(或偶极矩)大小M0(单位为N·m， 图8a和图8b)就成了震源强度的一个衡量标志， 并被称为地震的地震矩[3]。 对平面剪切错动震源， 力矩值M0的大小既与断层面积A有关， 也与断层平均错距D有关， 理论分析结果给出

M0=μAD

(1)

μ是震源区的剪切弹性模量， 或称剪切刚度。 如果由地震波观测得到了M0(例如， 由直达体波震源振幅谱的低频幅值可估算M0)， 再由余震空间分布估算出主震的断层面积A， 则由(1)式可推断震源断层的平均错距D。

地震距M0是个标量， 只是震源强度的一个量度。 震源的双力偶(或双偶极)力系还含有力的方向、 力臂的方向以及 “零轴” 方向等其他信息， 这种力偶系(含偶极力)既不是标量， 也不是矢量， 对它的完整描述需要用包含9个分量的二阶张量， 由于每个分量都表示特定力偶的力矩值， 因而该张量实际是产生地震的力矩张量， 通常就称为地震矩张量。 同一张量在不同坐标系中表达形式可能不一样。 例如， 在图8a所示的震源坐标系x-y-z中， 双力偶震源的地震矩张量M的表示式为：

(2)

而用图8b所示的等价偶极力系(也可看成是地震矩张量M的主轴坐标系， 或如图4a所示的T-B-P轴坐标系)的表示式则为：

(3)

这两个张量表达式的第2行第2列的元素总是为零， 这表示B轴(或z轴)方向无力的作用。 通常观测者看到的是在地平坐标下(如图4b， 震源位于坐标原点)表示的地震矩张量， 这时双力偶震源的地震矩张量也不会仅有两个非零元素了。

6 地震矩张量解 (moment tensor solution)

平面断层的纯剪切错动只是天然地震震源的近似表示。 实际的震源还常常含有其他变形成分， 如震源体积的整体膨胀或收缩、 某个方向的张裂或挤压变形等； 此外， 爆炸、 地层塌陷、 滑坡冲击等也可成为激发地震波的震源， 这类震源不宜用纯剪切错动模型来描述。 因而对多种震源的统一描述， 不是上述的震源机制解， 或双力偶点源模型的特定的地震矩张量解， 而是更普遍的地震矩张量解。 在一般坐标系x1-x2-x3下， 该张量含有9个分量[3]：

(4)

其中每个分量代表在选定的坐标系下表达的一个特定力偶(或力偶极)的力矩值(或偶极矩值)， 各分量具体含义表示在图9中。 由于震源是弹性体内部力系作用的结果， 角动量

图9 地震矩张量9个分量所表示的9种力偶[3]

守恒的条件要求(4)式表示的地震矩张量是对称张量， 即有M21=M12，M31=M13，M32=M23。

可以用多种方法将地震矩张量解分解为若干组成部分， 分解方法不是惟一的。 在地震矩张量M的主轴坐标系中(规定M1≥M2≥M3)， 一种常用分解法可表示为：

(5)

式中

(6)

这里MEXP是反映震源整体膨胀(负值表示收缩)强弱的偶极力的力矩值，MDC是双力偶成分的力矩值，MCLVD被专业人员称为补偿线性矢量偶极(compensated linear vector dipole, 简记为CLVD)， 它反映震源在主值M2方向发生张裂变形(负值表示挤压变形)、 而与M2垂直的各个方向发生相应收缩变形的强弱。

分析位于震源多个方位上的远近不同的台站观测到的地震体波或面波的波形记录， 可以推算出地震的地震矩张量解。 在用地震波形拟合方法测定天然地震的地震矩张量解时， 为容易得到稳定解答， 通常会利用M1

+M2+M3=0的约束条件， 这时的地震矩张量解只有5个独立分量， 没有震源整体的膨胀或收缩成分。 如果不加此约束条件， 地平坐标下的地震矩张量解将有6个独立分量值， 由它们可计算出地震矩张量的3个主值(张量的本征值)的大小和方向， 并进而分析出表示该震源的膨胀成分、 双力偶成分和补偿线性矢量偶极成分强弱的力矩值。 表2和图10给出了反演P波波形记录得到的地震矩张量解及其分解结果一例。 在求该地震矩张量解答时， 用了若干垂直向地震记录的P波初动方向作为约束条件。 由表2和图10可见， 该地震的震源有明显的体积收缩成分， 占了双力偶强度的25%， 在震源球投影图上表现为震源收缩区(P轴所在区)的范围比震源向外扩张区的范围大。

图10反演P波波形记录得到的1991年3月26日台湾东南近海6.5级地震的地震矩张量解。震源下半球等面积投影。圆点和圆圈表示波形反演中加的P波初动方向约束，粗实线表示实际P波节线在震源球上的位置，细实线表示矩张量解中分解出的双力偶成分的节线[4]

表2 1991年3月26日03:58:26.7台湾东南海域6.5级地震(深度15 km)的地震矩张量解

注：M1、M2和M3是地震矩张量解的3个主值；M0、MEXP和MCLVD分别是矩张量解的双力偶、 膨胀和补偿线性矢量偶极成分的力矩强度， 见(6)式，M0即MDC。

(作者电子信箱， 许忠淮： xuzh@cea-igp.ac.cn)

参考文献

[1] Steketee J A. Some geophysical applications of the elastically theory of dialocations. Canadian Journal of Physics, 1958， 36： 1168-1197

[2] Peter M Shearer. 地震学引论. 陈章立译. 北京： 地震出版社， 2007

[3] [美]安艺敬一， 理查兹 P G. 定量地震学， 理论和方法. 北京： 地震出版社， 1987

[4] 郑天愉， 姚振兴. 中国台湾以东地区地震矩张量研究及其构造意义. 地球物理学报， 1994， 37(4)： 478-486