探究一道波罗的海数学奥林匹克竞赛试题

●

(海南中学 海南海口 571158)

探究一道波罗的海数学奥林匹克竞赛试题

●李宁

(海南中学 海南海口 571158)

2011年波罗的海数学奥林匹克竞赛中有如下一道不等式试题：

题目设a,b,c,d是满足a+b+c+d=4的非负实数，证明不等式：

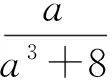
1 证法探究

这是一道常见类型的对称不等式题.由于已知条件是一次的，可以考虑“化曲为直”，用切线法证明.

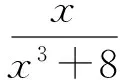
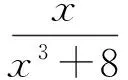
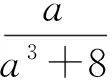
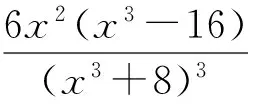
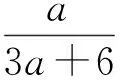
从而

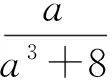
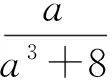
下面只需证明

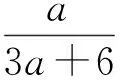
即

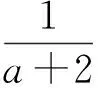
而由均值不等式

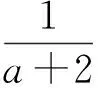
得

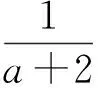
同理可得

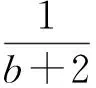
以上4个式子相加，得

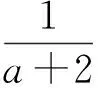
从而不等式得证.

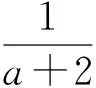
证法4当x≥0时，由九元均值不等式，得

于是

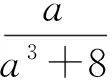
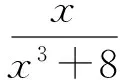
2 题目探究

上面探究了该试题的4种证明方法，同时对其题目本身也可作一番探究.

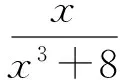
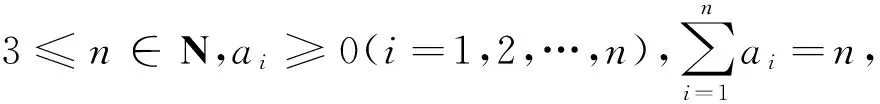
探究该试题的反向，得

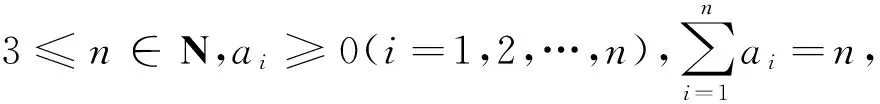
当ai中有一个为n其余全为0时,等号成立.

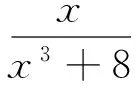
稍微改变该试题的条件，可得如下变式：

问题3设a,b,c,d是满足a2+b2+c2+d2=4的非负实数，则

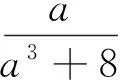
证明当x≥0时,

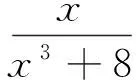
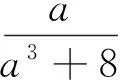
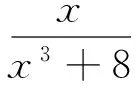
有兴趣的读者可以探究问题3的另证及推广.