对一道课本例题的深入挖掘

●

(金陵中学 江苏南京 210005)

对一道课本例题的深入挖掘

●严飞

(金陵中学 江苏南京 210005)

教材是学生获得系统知识的主要来源，它在教学中起着不可替代的作用.笔者认为在教学中指导学生对教材中的典型例题进行深入研究、引申推广，能起到事半功倍的效果：能充分调动学生的积极性与创造性，充分发挥学生的主体作用，引导学生进行探究性学习，并且有利于培养学生的灵活性与变通性，提高学生的思维品质，培养学生的创新意识与实践能力.

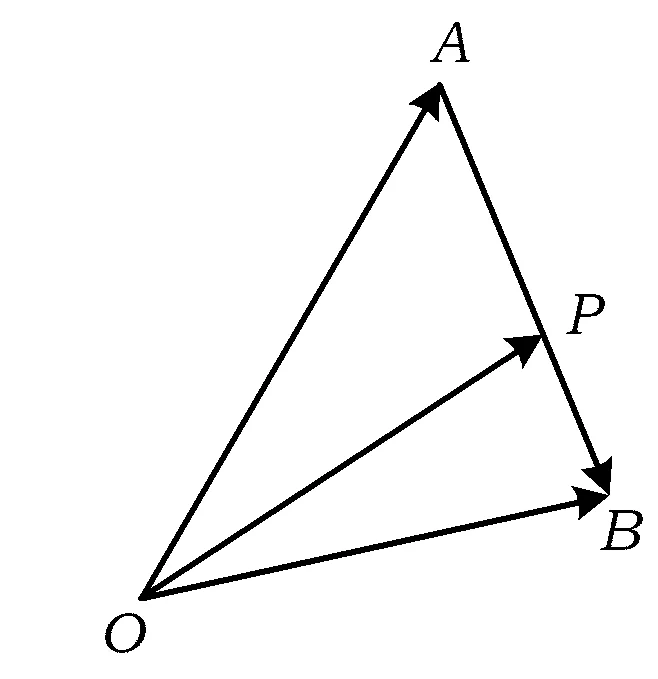
图1

在苏教版普通高中课程标准实验教科书《数学·必修4》“2.2.3向量的数乘”这一节中，课本定义了向量的数乘并给出了向量共线定理，此后安排了一个例题：

这道例题虽简单，内容却很丰富，学生也容易证明.但作为教师对这道题的认识不能仅仅停留在这个层面上，通过对这道例题的深入研究可以培养学生的发散思维能力，能让学生熟练掌握处理有关向量共线问题方法与技巧.

对本例有以下的思考：

还可以得到以下的推论：

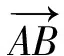
推论1和推论2揭示了平面上3个点共线的充要条件；推论3则沟通了向量共线定理与定比分点知识的联系.其中推论2还可以推广到空间：

推论4对空间任一点O和不共线的3个点A,B,C，点P与点A,B,C共面的充要条件是：存在实数x,y,满足

以上结论在解题中有着广泛的应用.

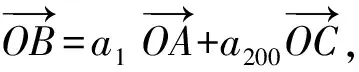
解法1由已知，得

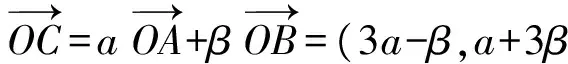
设C(x，y)，则

因为α+β=1，所以

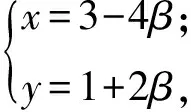
消去β，得点C的轨迹方程为

x+2y-5=0.

或由式(1)，得

代入α+β=1即得.

x+2y-5=0.

点评本题考查意图是解法2，但大多学生用的是解法1，这说明教材中传统的内容和方法在学生的头脑中还是根深蒂固的.教师不能仅习惯于用传统的思维方式去引导学生，这是问题的一个方面；另一方面，教师要对教材的例题进行更深入的钻研.

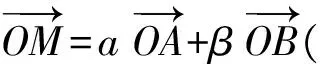
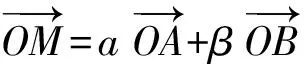
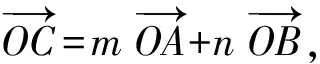
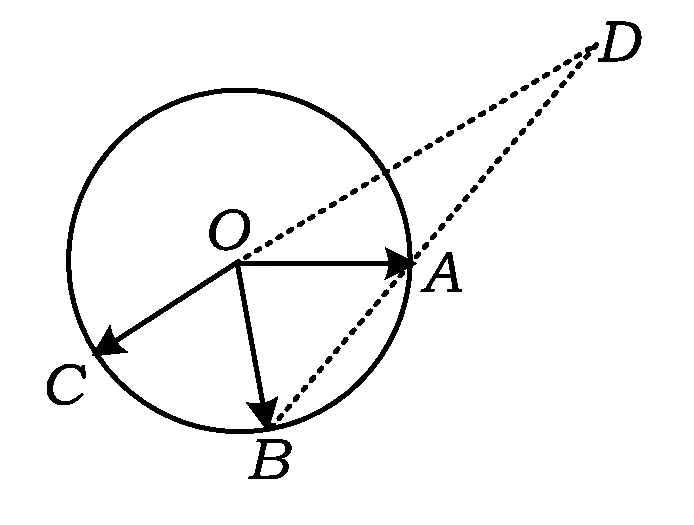
图2

解由点O，C，D共线，知

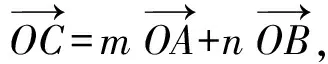
点评本题有一定的思考难度，充分利用题目中3个点共线的条件并结合推论2可以化难为易.

对教材的深入研究是增加内功的重要途径，题目千变万化，解题的过程就是知识组合的过程，但是很多题目都可以在教材中找到原型.只有深入地思考才能有所得，正是鉴于对教材的深入发掘，笔者得到了本文推出的一系列推论,也领悟到一个道理：不思则无，深思则远，远思则宽.学生的学习是如此，同样教师的教学也是如此.只有善于思考，我们的认识才能上升到理性的高度，才能触及事物的本质.

总之，认真钻研教材,真正用好课本中已经提供的素材，通过各种不同的处理方法,有的放矢地组织教学,将是一个值得关注和潜心研究的课题.

[1] 单墫．普通高中课程标准实验教科书(数学·必修4)[M]．江苏：江苏教育出版社，2012：68-71．

[2] 张定强，赵宏渊，杨红．高中生数学反思能力培养的基本模式与实践探索[J]．数学教育学报，2008，17⑴：38-42．