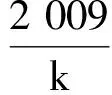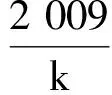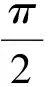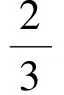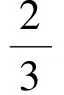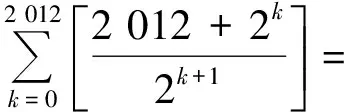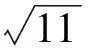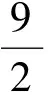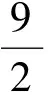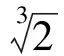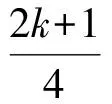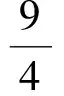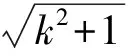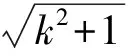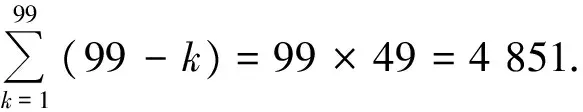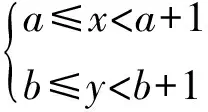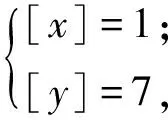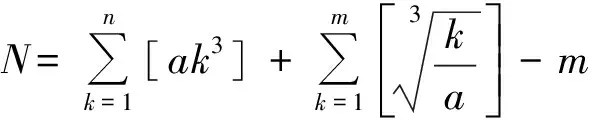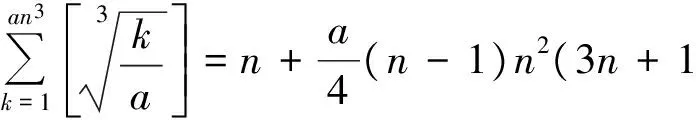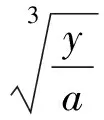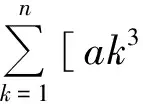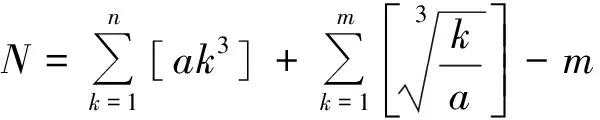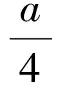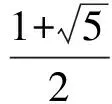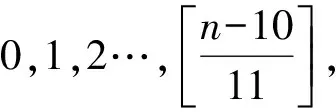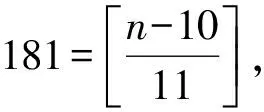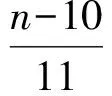高斯函数——朴素的外形、深邃的内涵

●

(柯桥中学 浙江绍兴 312030)

高斯函数
——朴素的外形、深邃的内涵

●章水云

(柯桥中学 浙江绍兴 312030)

高斯函数从形式上看，简洁美观；从函数角度看，包含着连续和离散2个方面，因此高斯函数有其独特的魅力.与高斯函数有关的数学问题，历来被各级竞赛命题者青睐，是各级竞赛的热点问题且常考常新.本文试图对高斯函数的性质及应用作一个比较全面的概括，现分述如下：

1 高斯函数y=[x]的定义和性质

1.1 定义

设x∈R，用[x]表示不超过x的最大整数，则称y=[x]为高斯函数，也叫取整函数.记{x}=x-[x]为x的小数部分.高斯函数从形式上看，简洁美观，易为学生理解，而从函数角度看，其定义域为R，值域是Z，因高斯函数的定义域是连续的，值域却是离散的，它关联着连续和离散2个方面，故有其独特的性质和广泛的应用.

1.2 性质

(1)当x1≤x2时，[x1]≤[x2].

(2)[n+x]=n+[x]，{n+x}={x}，其中n∈Z.

(3)x-1<[x]≤x<[x]+1.

(4)若[x]=[y]=n，则x=n+a,y=n+b,其中0≤a<1，0≤b<1.

(5)对于一切实数x,y，有

[x]+[y]≤[x+y]≤[x]+[y]+1.

(6)若x≥0,y≥0，则[xy]≥[x][y],特别地，[nx]≥n[x]，其中n∈Z.

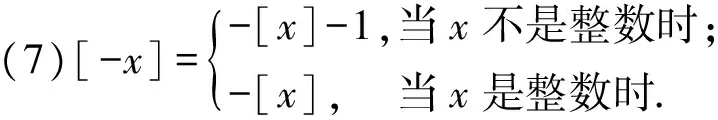
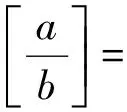
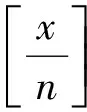
(11)设p为任一素数，在n!中含p的最高乘方次数记为p(n!)，则

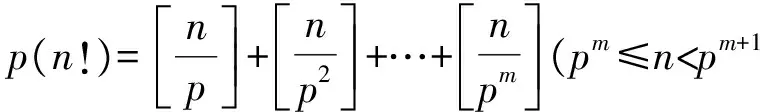
(12)函数y=[x]的图像如图1所示，设f(x)={x}，则f(x)是周期为1的函数，图像如图2所示.

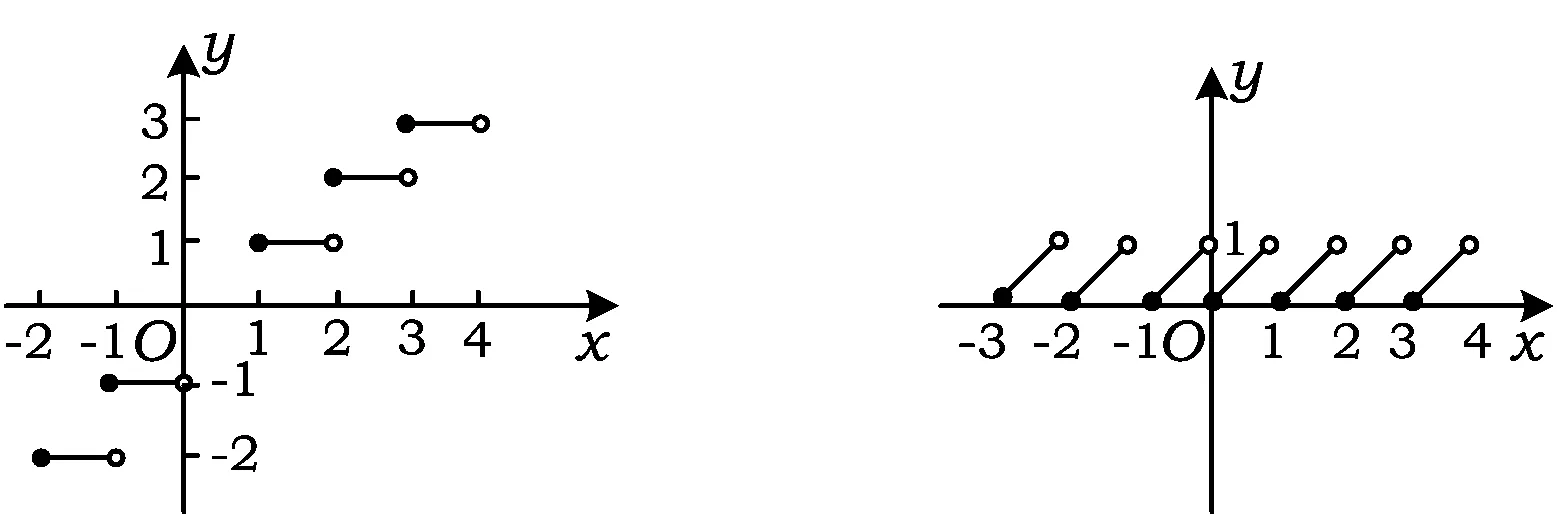
图1 图2

2.高斯函数的应用

2.1 利用高斯函数解决整数问题

(2009年全国高中数学联赛河北省预赛试题)

分析当0

[x+y]=[x]或[x+y]=[x]+1；

当y≥1时，

[x+y]>[x].

又因为

即

(1993年全国高中数学联赛试题)

分析令x=1031，则

2.2 利用高斯函数解决求值问题

例3设[x]表示不超过x的最大整数，则[sin1]+[cos2]+[tan3]+[sin4]+[cos5]+[tan6]=______.

(2011年全国高中数学联赛贵州省预赛试题)

[sin1]+[cos2]+[tan3]+[sin4]+[cos5]+[tan6]=

0+(-1)+(-1)+(-1)+0+(-1)=-4.

例4符号[x]表示不超过x的最大整数，符号{x}表示x的小数部分，即{x}=x-[x].若实数x满足[2x]+[4x]+[6x]+[8x]=2 012，则{x}的最小值为______.

(2012年福建省高一数学竞赛试题)

分析由题意x=[x]+{x}，记{x}=t，0≤t<1,则

[2x]+ [4x]+[6x]+[8x] =

20[x]+[2t]+[4t]+[6t]+[8t]=2 012.

由0≤t<1,得

[2t]+[4t]+[6t]+[8t]=12，

[2t]+[4t]+[6t]+[8t]<1+2+4+5=12，

例5[x]表示不超过实数x的最大整数，则[log21]+[log22]+[log23]+…+[log22 012]=______.

(2012年全国高中数学联赛河南省预赛试题)

分析根据题目特征，联想到当2k≤x<2k+1时，[log2x]=k,从而

[log21 024]= [log21 025]+…+[log22 012]=

10(2 012-1 023)=9 890.

又[log21]+[log22]+…+[log21 023]=

1·(22-21)+2·(23-22)+…+9·(210-29)=

1·2+2·22+…+9·29=8 194,

因此

[log21]+ [log22]+…+[log22 012]=

8 194+9 890=18 084.

(2012年全国高中数学联赛湖北省预赛试题)

分析注意到2 012=211-25-22,因此

(210-24-2)+(29-23-1)+(28-22)+

(27-2)+(26-1)+(25-1)+24+23+

22+2+1=2 012.

2.3 利用高斯函数解决方程问题

例7对任意的x∈R，[x]表示不大于x的最大整数，则满足[|x2-1|]=10的x的集合是

( )

(2009年全国高中数学联赛山东省预赛试题)

分析因为[x]≤x<[x]+1，所以

10≤|x2-1|<11.

当x2≤1时，10≤x2-1<11无解.

当x2>1时，10≤x2-1<11，解得

故选C.

(2009年全国高中数学联赛福建省预赛试题)

分析显然x>0.若x≥3，则[x]≥3，从而

不符合要求；若0

不符合要求.

(2010年全国高中数学联赛福建省预赛试题)

分析根据高斯函数性质(3)，当x≥3时，

x3-3[x]≥x3-3x=x(x2-3)≥3·6=18，

不符合要求；

当x≤-3时，

x3-3[x]

-3·6+3=-15，

不符合要求.

(2011年全国高中数学联赛四川省预赛试题)

分析题目中定义「x⎤和高斯函数是姊妹定义，或者说灵感来源于高斯函数，故本题的解题思路可作相同的类比、迁移.

于是原方程等价于

即

得

2.4 利用高斯函数解决格点问题

格点，又称整点，就是平面直角坐标系中横坐标和纵坐标都为整数的点.格点问题是一类有趣的数学问题，往往与[x]有关.

例11双曲线x2-y2=1的右半支与直线x=100围成的区域内部(不含边界)整点(纵、横坐标均为整数的点)的个数是______.

(2010年全国高中数学联赛试题)

分析由对称性，知只需考虑x轴上方的情况.设y=k(k=1,2,…,99)与双曲线右半支交于Ak,交直线x=100于Bk，因此

则线段AkBk内部整点的个数为

从而在x轴上方区域内部整点的个数为

又因为在x轴上有98个整点，所以整点的个数为

2×4 851+98=9 800.

例12[x]表示不超过实数x的最大整数值，则在平面直角坐标系xOy中，满足[x]·[y]=2 013的所有点(x,y)组成的图形面积为______.

(2012年全国高中数学联赛新疆维吾尔自治区预赛试题)

2 013=1·2 013=3·671=11·183=33·61，

所以满足[x]·[y]=2 013的所有点(x,y)组成的图形是16个面积为1的区域，其面积为16.

例13设[x]表示不超过实数x的最大整数，则在平面上，由满足[x]2+[y]2=50的点所形成的图形的面积是______．

(2011年全国高中数学联赛甘肃省预赛试题)

分析同上例，设[x]=a,[y]=b.在平面上，由满足[x]2+[y]2=50的点所形成的图形关于x轴、y轴对称，因此只需考虑第一象限的情况.因为

50=1+49=25+25=49+1，

所以

在第一象限所形成的图形面积为3.因此在平面上，由满足[x]2+[y]2=50的点所形成的图形的面积是12.

例14(1)设a>0，平面上的点如果其坐标都是整数，则称之为格点.今有曲线y=ax3过格点(n，m)，记1≤x≤n对应的曲线段上的格点数为N.证明：

(2)进而设a是一个正整数，证明：

(注：[x]表示不超过x的最大整数.)

(2010年全国高中数学联赛浙江省预赛试题)

(2)当a是一个正整数时，曲线y=ax3上的点(k,ak3)(k∈N+,1≤k≤n)都是格点，因此第(1)小题中的N=n.同时，m=an3.将以上数据代入第(1)小题的结论，得

2.5 构造高斯函数解决问题

在求解一些问题时，若能根据题目特征、解题过程积极联想，合理地构造、利用高斯函数及其性质，往往能使问题更轻松地解决.

例15一个正数，若其小数部分、整数部分和其自身成等比数列，则该数为______．

(1989年全国高中数学联赛试题)

分析记这个数为x(x>0)，则其整数部分为[x]，小数部分为{x}=x-[x].由题意得

[x]2=(x-[x])·x，

从而

[x]2

得

[x]2-[x]-1<0，

解得

由x>0知[x]=1,从而

1=(x-1)·x，

即

x2-x-1=0,

故

例16设n≥11是一个正整数，由不大于n的连续10个正整数的和组成集合A，由不大于n的连续11个正整数的和组成集合B.若A∩B的元素个数是181，求n的最大值和最小值.

(2011年全国高中数学联赛甘肃省预赛试题)

分析显然，

A={55+10k|0≤k≤n-10,k∈Z},

B={66+11l|0≤l≤n-11,l∈Z},

为求A∩B的元素个数，令55+10k=66+11l，则

10k=(l+1)·11.

即

2 001≤n<2 012，

于是n的最大值和最小值分别为2 011和2 001．

通过本文可以看到高斯函数是各类竞赛的“常客”.高斯函数的外表朴素，定义简单，性质也不多，但正因为如此，在解题时常无规律可循，需要我们结合分类讨论、数形结合、转化、化归等思想和方法.