一道希望杯培训题的探究

●

(锦屏中学 浙江奉化 315500)

一道希望杯培训题的探究

●傅前达

(锦屏中学 浙江奉化 315500)

第23届希望杯全国数学邀请赛培训题初一年级第69题：

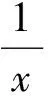
从学生的练习解答情况看，大多数填“1”．课堂上分析此题时，请学生介绍了各自的思路、解法，很受启发．

学生1：用特殊值法，令x=y=z=w=1，使连等式成立，因此w2x2y2z2=1．

有学生质疑：此解法不符合条件(要求w,x,y,z互不相等)，且选取不同的特殊值，结果可能不同．答案正确纯属巧合．

学生2：这是一个不定方程组，有无数组解，可以用某个未知数的代数式表示其他未知数，再代入求解．对于客观题，我尝试用赋值法，减少运算量．

令x=1，则

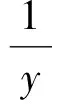
解得

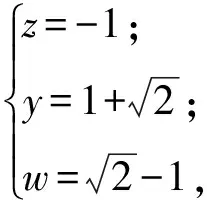
从而

wxyz=-1,

即

w2x2y2z2=1．

(该生有非常扎实的代数基础知识和基本技能.)

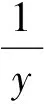
学生3：根据经验，轮换式通常整体考虑，采取全加、全乘的策略，我尝试后，没有成功．联想起一道轮换式竞赛题，是用轮减法解决的，模仿后居然有了惊喜．

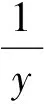
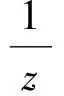
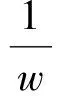
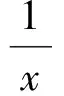
全乘得

(w-x)(x-y)(y-z)(z-w)=

因为(w-x)(x-y)(y-z)(z-w)≠0，所以

w2x2y2z2=1．

(此法与组委会提供的参考解法一致，此学生的数学素养可见一斑.)

学生4：顺着前一种解题的思路，我进行了简化操作．

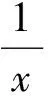
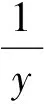
式(1)，式(2)相乘,得

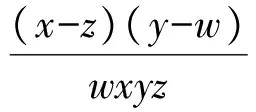
因为(w-y)(x-z)≠0，所以

wxyz=-1，

从而

w2x2y2z2=1．

(教室里先是鸦雀无声，很快响起了热烈的掌声，学生们由衷钦佩的目光聚焦在这位学生的身上.)

在课后的反思中，笔者联想起了2003年全国初中数学联赛的最后一题：

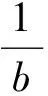
该题在起初求解时遇到了极大的困难，通过辗转代换消元，历经复杂的运算、因式分解、分类讨论解答．如果采用学生4的结论，结合学生3的经验，可以这样解答：

解全乘得

轮乘后再全加,得

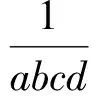
又因为abcd=-1，所以

x4-4x2+4=0，

解得

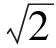
回顾本题的解决过程，学生始终处于舞台的中央，真正成为学习的主人.学生热情高涨，积极参与到数学活动中去，独立思考、自主探索、合作交流、共同发展，体验到了数学的魅力、思维的乐趣，增强了自信心．教师成为了组织者、合作者、学习者，同样收获颇丰：在数学资优生培养中，要相信学生，放手让学生自主学习，大胆尝试先学后教，即先布置学习任务独立探索，再在课堂上让学生畅所欲言，教师认真听，积极捕捉学生的闪光点，放大并完善它，若能有画龙点睛之举则更妙．