基于虚拟参考迭代整定方法的永磁同步电机优化重复控制

聂成翔， 陈志盛

(长沙理工大学可再生能源电力技术湖南省重点实验室，湖南长沙410076)

永磁同步电机运行原理与普通电激磁同步电机相同，但它以永磁体代替了激磁绕组，提升了电机运行的可靠性［1-2］。20世纪60年代以后，永磁同步电机开始应用于交流变频调速系统，到20世纪80年代后，由于新型电力电子器件的不断涌现，极大地促进了永磁同步电机调速系统的发展。

FRIT即虚拟参考迭代整定［3］，它是一种专门用来设计未知模型反馈控制器的，它能优化其性能指标，包括虚拟参考的一次性实验输出计算，使其系统性能得到相对稳定等。对于对象模型未知的系统，以及周期信号在测量不到的情况下，FRIT具有很大的运用空间。

重复控制是一种以内模原理为基础的控制策略［4］。内模原理就是如果想让控制系统对某一参考指令实现无静差跟踪，那么该参考指令的模型必须包含在稳定的闭环控制系统内部。如果伺服系统［5］要满足对稳定性和动态性能的鲁棒性，即当系统参数发生变化时仍能保持稳定性、稳态偏差为零和过渡响应不受参数变化的影响，那么设计的重复控制器就可以解决问题。

1 永磁同步电机调速系统数学模型

如图1所示，基于矢量控制的永磁同步电机调速系统主要由电流检测、转速和位置检测、坐标变换、空间矢量脉宽调制(SVPWM)、电流调节器、转速调节器等环节组成［6］。系统中的电流环和转速环通常采用PID型算法控制。

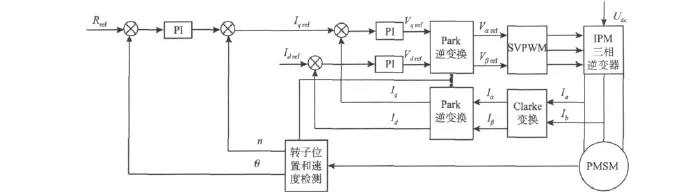
图1 永磁同步电机矢量控制原理Fig.1 PMSM vector control principle diagram

当永磁同步电动机结合矢量控制法作为被控对象时，常用其d-q轴下的数学模型进行分析，其定子磁链方程为

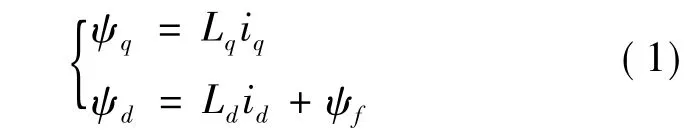
定子电压方程为

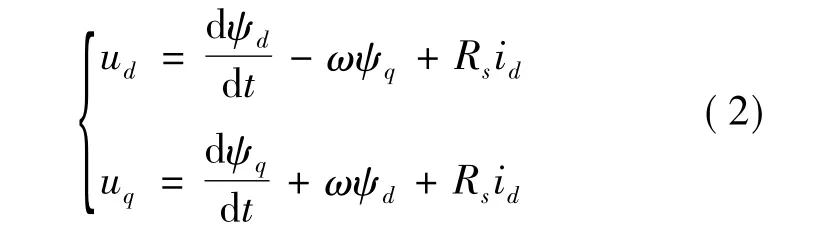
其中:Rs为电枢绕组电阻;Lq，Ld分别为d，q线圈的等效绕组电感;ψf为永磁体产生的等效磁链，其值为常数;id，iq为定子电流合成矢量在d，q轴上的分量;ω为转子电角速度。

永磁同步电机的运动方程为

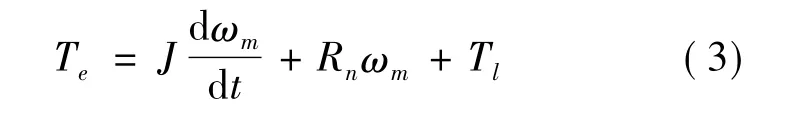
其中:Tl为负载转矩，正方向与Te相反;Rn为运动阻尼系数;J为电机与负载转动惯量之和;ωm为转子机械角速度，其中机械角速度与电角速度的关系为ω =npωm;Te与ωm的正方向相同。

2 基于FRIT的重复控制器设计

2.1 重复控制器设计原理

重复控制是基于内模原理的一种控制方法。Francis和Wonham［7］提出的内模原理，在伺服系统控制中起着相当重要的作用。内模原理是指如果在一个稳定的闭环系统内设置一个可以产生与参考输入信号相同的信号发生器，则系统输出可以无稳态误差的跟踪输入指令。Inoue［8］等人基于上述思想提出了重复补偿控制理论［9-10］，利用内模原理，在稳定闭环系统内设置一个可以产生与参考输入同周期的内部模型，从而使系统实现对外部周期参考信号的渐近跟踪。

图2为简单的单输入、单输出闭环系统。

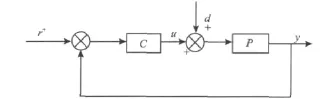
图2 基本闭环系统Fig.2 Basic closed loop system

由图2不难看出，这是一个单输入、单输出、连续时间且时间不变的闭环系统。注意到C(ρ)为PID控制器中的反馈控制器，其表达式:

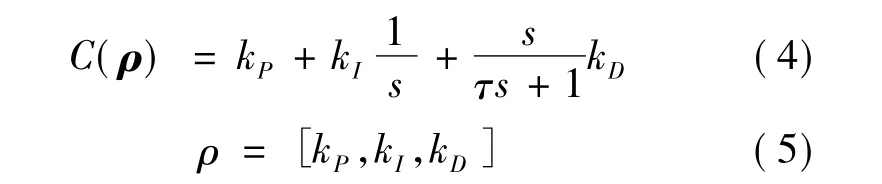
其中，kP，kI，kD分别为比例、积分、微分增益项，τ 是个很小的正实数，令u0，y0是此系统的输入输出，当参考信号τ应用于闭环系统时，C(ρ0)成立，其中ρ0是一个控制器的初始参数向量，假定控制器C(ρ0)闭环稳定，且ρ0保持不变。

为减小跟踪误差，有效地增大运行带宽，提出改进型重复控制器，P为控制对象，C为PID控制器，r为输入，y为输出，d为外部扰动。此外，参考模型的扰动响应Pdr和参考模型的输出扰动d中有关系式ydr=Pdrd。那么在模型不确定时系统的初始输入输出数据u0，y0由虚拟信号的输入得到。但是此系统的跟踪性仍然不很精确，加之存在外部输入扰动信号时，系统不能得到很好的抑制。为了使此系统减小不确定干扰而造成的输出畸变，使得稳态下输出能很好地跟踪参考信号，设计了一个插入式的重复补偿控制器如图3所示。

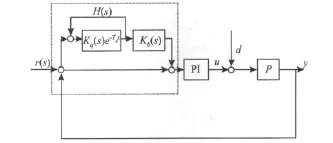
图3 改进型重复控制系统Fig.3 Improved repeat control system

图3中虚线部分的传递函数为

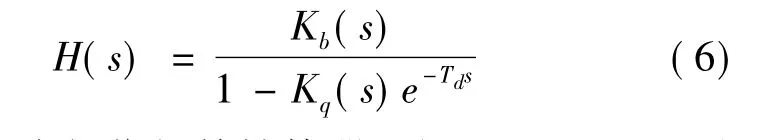
其中，Kb(s)为相位超前补偿器。设 Kb(s)=eτbs，这里τb是非负常数。Kq(s)为一个低通滤波器，Td为滞后时间，其取值与期望输入信号的周期相同。低通滤波器Kq(s)仅允许输入信号特定的谐频通过，受低通滤波器带宽ωq的限制，重复控制系统的跟踪误差在稳态时不可能为零。

改进后的重复控制系统，由于插入了一个重复补偿控制器，使得稳态输出下能快速精确地跟踪参考信号，系统的精确性和快速性得到了很大地提升。

2.2 FRIT整定PID扰动衰减

FRIT中引入了虚拟参考信号，从图3中可得到

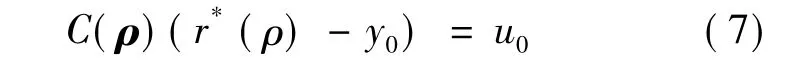
虚拟参考信号r*(ρ)转化得到

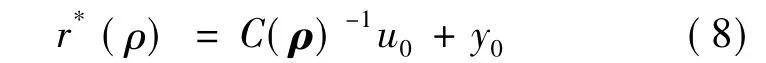
式中，y0设定为闭环系统的输出，C(ρ0)在理想的扰动响应下且虚拟信号r*(ρ)是增强的，因此，由公式(8)得到

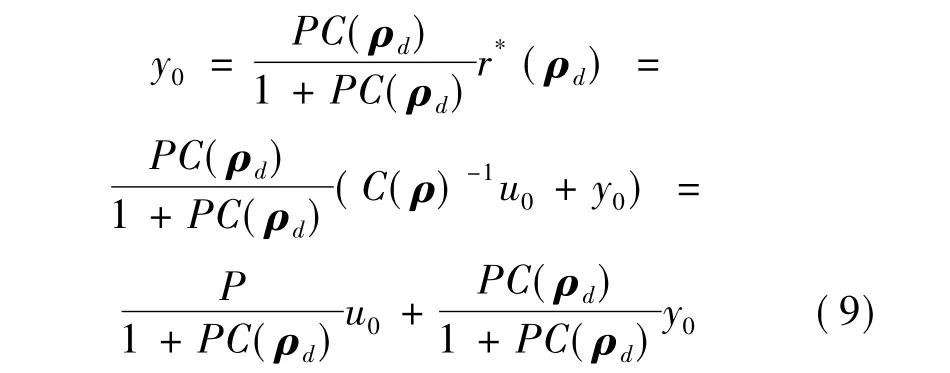
假设存在参数向量ρd做为理想控制参数向量，那么闭环传递函数中从扰动d到输出y符合参考扰动响应模型，即等式假设成立。令Pr是参考模型的理想参考信号响应，ρd是存在Pr的闭环系统中理想控制器的参数向量，Pr即满足

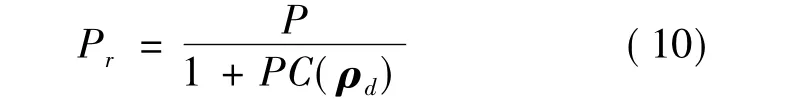
因此式(9)可以转化为

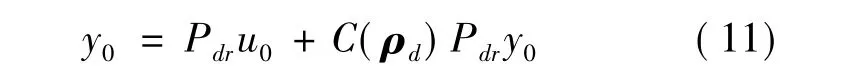
FRIT验证理想控制器参数向量ρd是根据公式(11)与模型中的一次实验输入输出数据u0，y0得到的。令

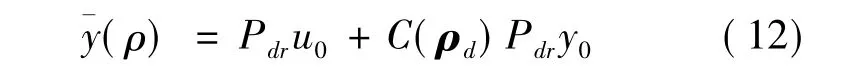
为了获得最小的优化控制器参数向量，对¯y(ρ)和y0采用积分平方误差的方法求得

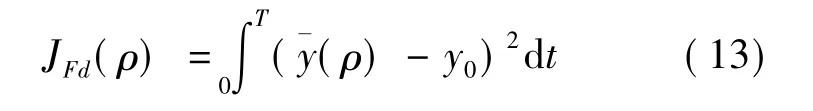
其中优化参数向量为

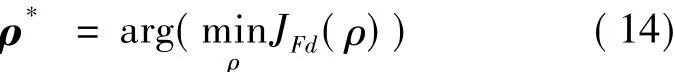
3 数值仿真与分析

通过以上对FRIT算法的推导，由公式(4)，(12)可以得到FRIT优化算法的整体模型如图4所示。

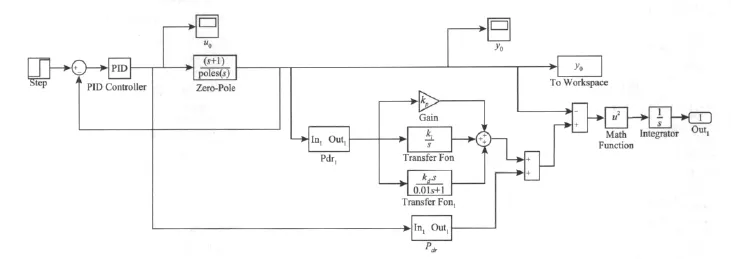
图4 FRIT算法模型Fig.4 FRIT algorithm model

对于PID控制的FRIT优化参考模型，假定不确定对象模型P(s)可以表示为

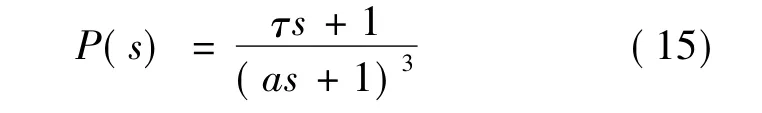
其中a=1，为一个很小的常数;y0和u0假定为在存在扰动信号r下闭环系统的初始输出输入数据，且初始PID参数定义为kP=0.5，kI=0.5，kD=0.2，初始PID增益的输入输出数据如图5所示。

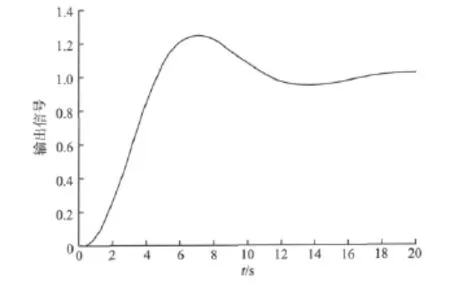
图5 初始PID参数扰动响应Fig.5 Initial PID parameters disturbance response curve

假定参考模型Pdr(s)定义为

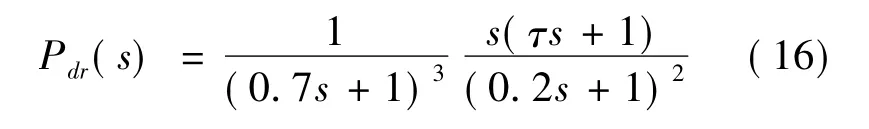
且PID控制器的参数设定为kP=2.427 1，kI=0.999 9，kD=1.507 1。图6为PID参数调整后的扰动响应曲线图。

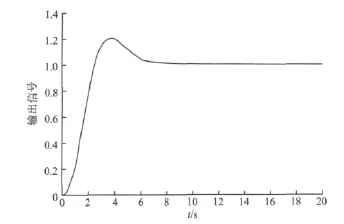
图6 PID参数调整后扰动响应Fig.6 Initial PID parameters disturbance response curve

对于永磁同步电机模块电机参数设置为:额定转速ne=1 000 r/min，额定转矩Te=2 N·m，额定功率Pe=8 000 W，额定电压Ue=380 V，同步电感Ld=8.5×10-3H，定子相绕组电阻R=5.57 Ω，转动惯量J=0.8×10-3kg·m2，转子磁通ψf=0.243 Wb。

通过永磁同步电机的仿真模型能得到转速、转矩和相电流的相应曲线如图7～9。

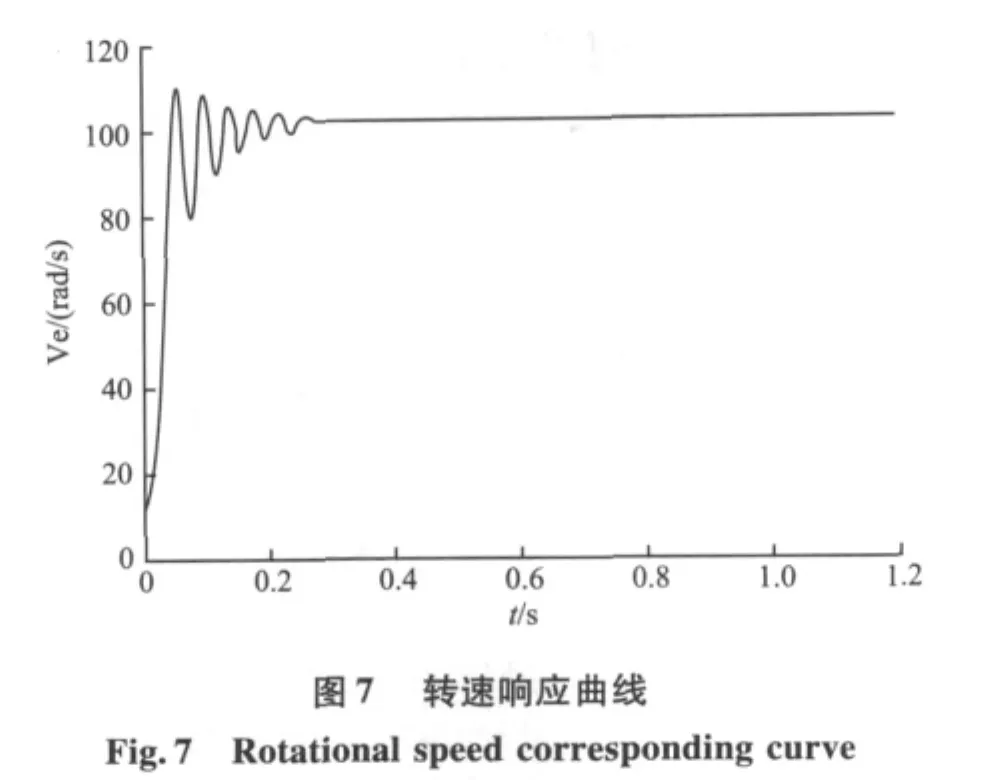
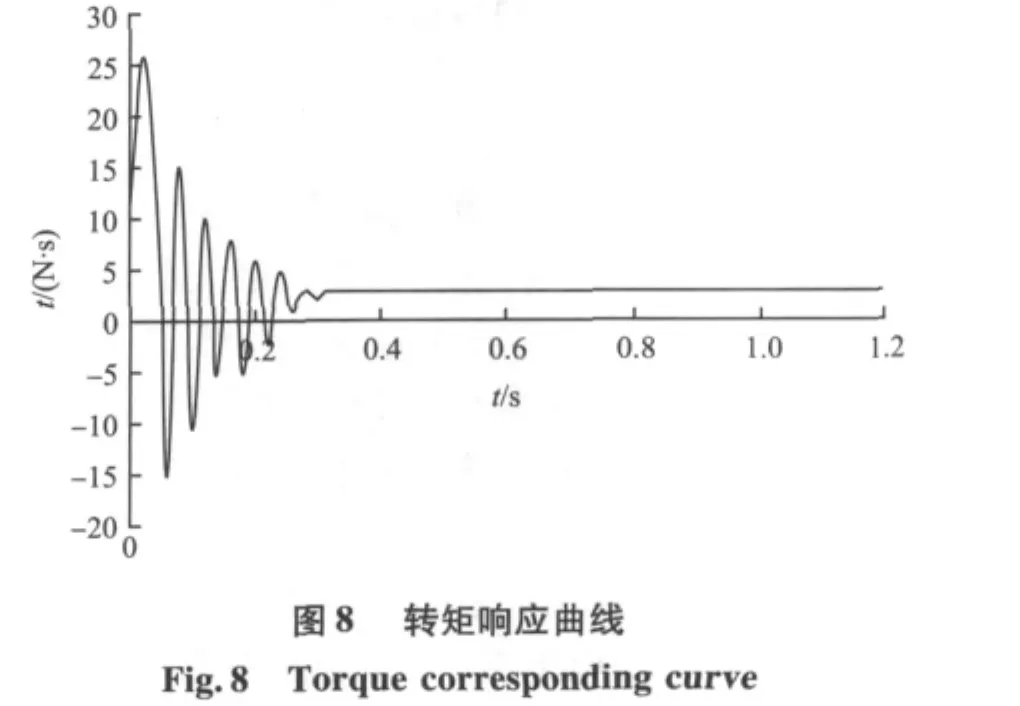
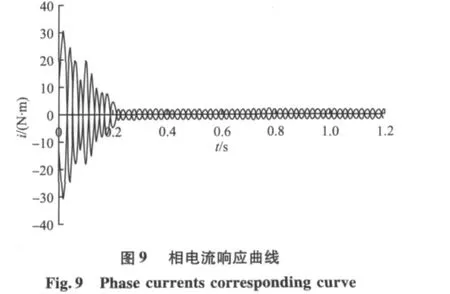
从转速和转矩响应曲线可以看出，转速和转矩在很短的时间内就达到了稳定值，虽然有轻微波动，但不影响整个系统。相电流曲线开始时电流值比较大，但很快达到设定值。通过仿真结果可以看出，系统能平稳运行，具有较好的静、动态特性。

4 结语

针对永磁同步电机系统进行研究，运用虚拟参考迭代整定方法(FRIT)整定PID控制器参数，最后在Matlab/Simulink仿真下证明系统的扰动性能得到了很大的改善，并且由PMSM的转速、转矩、相电流等的仿真曲线图看出系统能快速稳定，具有较好的静、动态特性。通过仿真可知，当对象模型或者周期信号未知的情况下，正确运用FRIT方法能使问题得到很好的解决。

［1］Hjalmarsson H，Gevers S M.Gunnarsson，Lequin O.Iteretive feedback tuning:theory and applications［J］.IEEE Control Systems Magazine，1998，18:26-41.

［2］Ogawa M，Kano M.Practice and challenges in chemical process control applications in Japan［C］//IFAC World Congress.Seoul，Korea:［s.n.］，2008:10608-10613.

［3］Kaneko O，Yoshida K，Matsumoto K，et al.A new parameter tuning for controllers based on least-squares method by using one-shot closed loop experimental data an extension of fictitious reference iterative tuning［J］.Trans of Institute of Systems，Control，and Information Engineering，2005，18(11):400-409.

［4］Campi M C，Savaresi S M.Direct nonlinear control design:the virtual reference feedback tuning(VRFT)approach［J］.IEEE Trans On Auto matic Control，2006，51(1):14-27.

［5］陈宗云.基于DSP的永磁同步电机伺服系统的研究［D］.杭州:浙江工业大学，2006.

［6］缪天舒，王隆太，许晓峰.基于重复控制的数控系统伺服调节技术的研究［J］.机械科学与技术，2008，6(27):838-840.

MIAO Tian-shu，WANG Long-tai，XU Xiao-feng.Repeat the numerical control system based on control servo regulation technology［J］.Mechanical Science and Technology，2008，6(27):838-840.(in Chinese)

［7］马训鸣，林晓焕.模型参考和重复控制在电液伺服同步加载系统中的应用研究［J］.机床与液压，2009，10(37):178-180.MA Xun-ming，LIN Xiao-huan.Model reference and repeat electro-hydraulic servo control in the application of synchronous loading system［J］.Machine Tool and Hydraulic Pressure，2009，10(37):178-180.(in Chinese)

［8］白华煜，刘军，楚小刚.基于模糊控制永磁同步电机直接转矩控制研究［J］.电气传动，2005，35(5):6-9.

BAI Hua-yu，LIU Jun，CHU Xiao-gang.Based on the fuzzy control permanent magnet synchronous motor direct torque control study［J］.Electric Transmission，2005，35(5):6-9.(in Chinese)

［9］张立强.基于自适应模糊PID的径向柱塞变量泵电液伺服控制［D］.兰州:兰州理工大学，2003.

［10］王春行.液压伺服控制系统(第2版)［M］.北京:机械工业出版社，1993.