新型线性函数光子晶体的光子二极管

张斯淇，吴向尧，刘晓静，巴 诺，王 婧，李 宏，马 季，董 赫，陈万金，尹新国，郭义庆

(1.吉林师范大学物理学院，吉林四平136000;2.淮北师范大学物理学院，安徽淮北235000;3.中国科学院高能物理研究所，北京100049)

自Yablonovitch［1］和John［2］提出光子晶体概念以来，光子晶体的光学传输特性研究已引起人们广泛关注［3-10］.一维光子晶体结构简单，易于制备，并具有全方向的三维能隙结构［11］，因此用一维光子晶体材料可制备出二、三维光子晶体材料制作的器件.

文献［12］首次提出了函数光子晶体的概念，即介质折射率是空间位置的函数，但要求折射率在两端点处相等，因此是一种特殊函数光子晶体.本文在此基础上，提出一般函数光子晶体，即折射率是空间位置的任意函数.在线性折射率函数的一维函数光子晶体中，研究其透射率和不同周期数及光学厚度对电场强度的影响.

1 光在一般函数光子晶体中的运动方程

一般函数光子晶体介质层的折射率是一个随空间位置变化的周期函数，设 n(z)，n(x，z)，n(x，y，z)分别表示一维、二维和三维函数光子晶体的折射率.

光在一维函数型介质中的传播路径如图1所示.由图1可见，其运动轨迹在xz平面上为曲线.当入射光入射至介质分界面A点时，曲线AB和BC分别表示光在介质中的入射路径和反射路径.

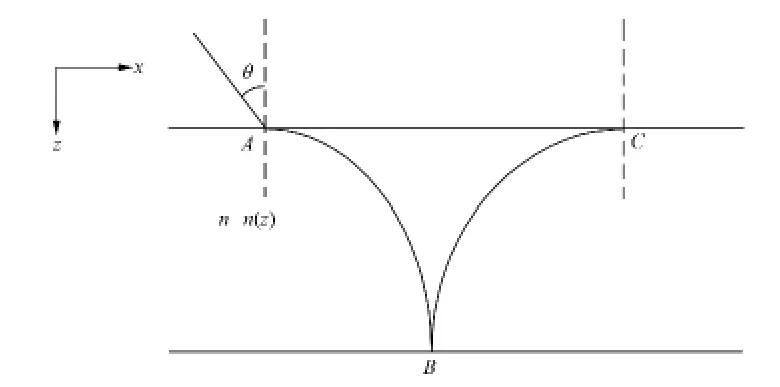
图1 光在一维函数型介质中的传播路径Fig.1 Motion path of light in the medium of one-dimensional function

光的运动方程可由费马原理求得

在二维传播空间中，线元ds为

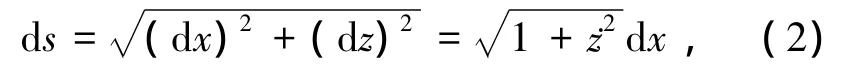
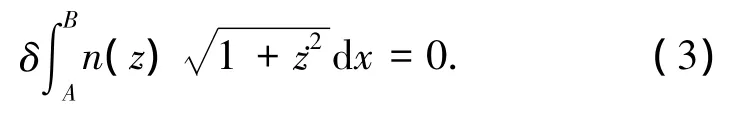
将方程(3)转换为

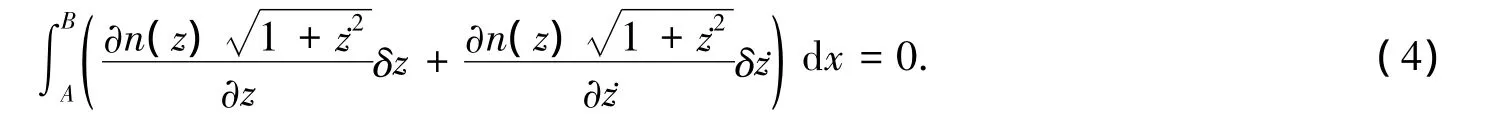
由于A，B两个端点的变化为零，即δz(A)=δz(B)=0，因此对于任意变量dz，方程(4)可转换为

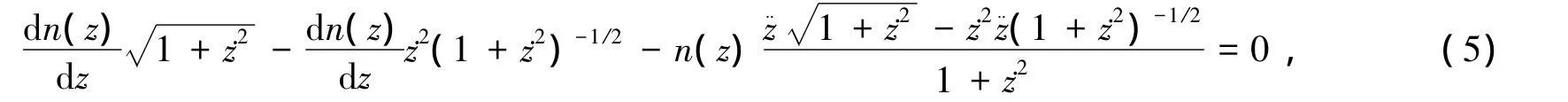
简化方程(5)可得

方程(6)即为光在一维函数型介质中的运动方程.

2 光在一维一般函数光子晶体中的传输矩阵

设空间有一介质层B，其折射率分布函数为n(z)，厚度为b.若电场E的偏振与入射面垂直(TE波)，则由电场和磁场的边值关系可知，介质交界面切向方向上的电场强度和磁场强度连续，如图2所示，其中E0和H0为在界面Ⅰ上侧的场矢量，EⅠ和HⅠ为在分界面Ⅰ下侧的场矢量，EⅡ和HⅡ为在界面Ⅱ下侧的场矢量.在界面Ⅰ附近电场分量包括入射光波Ei1、透射光波Et1、反射光波Er1和从界面Ⅱ反射到界面Ⅰ的光波

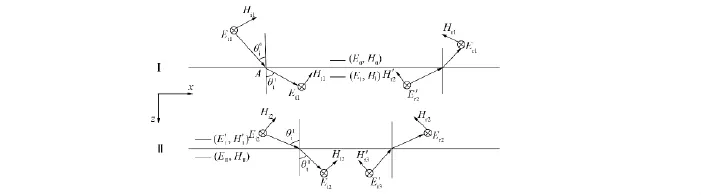
图2 光在任意介质层中的传播Fig.2 Light transmission in an arbitrary middle medium

由电场和磁场的边值关系可知，对于界面Ⅰ两侧的电场强度和磁场强度在切向方向上的分量是连续的，即

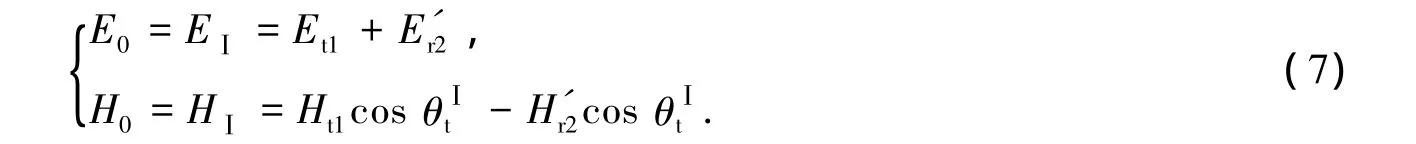
界面Ⅱ两侧的电场强度和磁场强度在切向方向上的分量可表示为

其中电场强度Et1和Ei2分别为

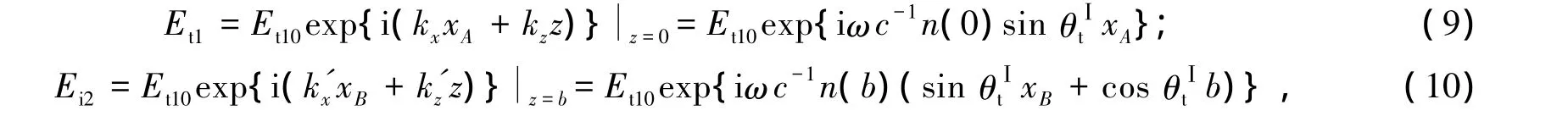
其中:xA和xB分别为x在A，B两点的坐标分量;b为介质厚度.

将方程(6)两边积分

可得

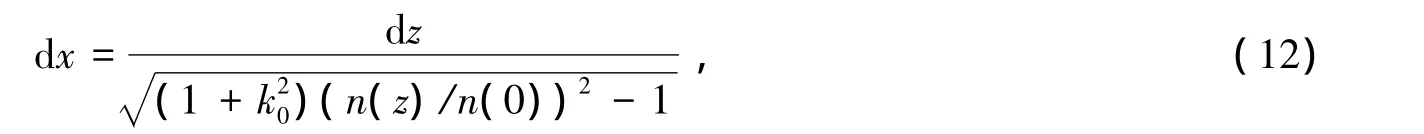
其中 k0=cot.

将方程(12)两边积分可得坐标分量xB为

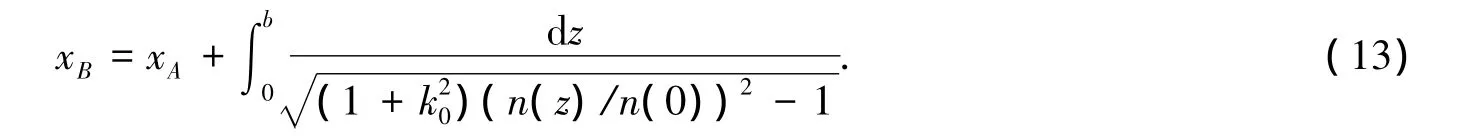
将方程(9)，(13)代入方程(10)中，并利用折射定律

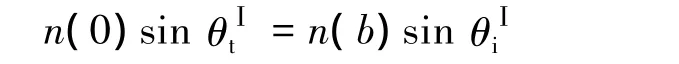
可得

其中

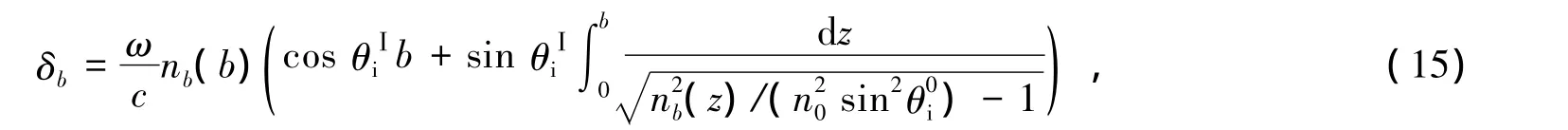
n0为空气折射率，和分别为界面Ⅰ和Ⅱ的入射角.同理可得

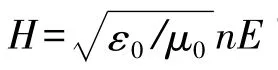
其中:

3 一维一般函数光子晶体的结构及其电场分布

由于光子晶体包含2种不同折射率介质，因此其折射率在2个介质的分界面处不连续.本文设计一维一般函数光子晶体结构如图3所示.在第一个半周期介质B中，其折射率分布函数为nb(z)，在第二个半周期介质A中，其折射率分布函数为na(z)，介质厚度分别为b和a.方程(18)为半个周期介质B的传输矩阵，则另半个周期介质层A的传输矩阵为

其中:

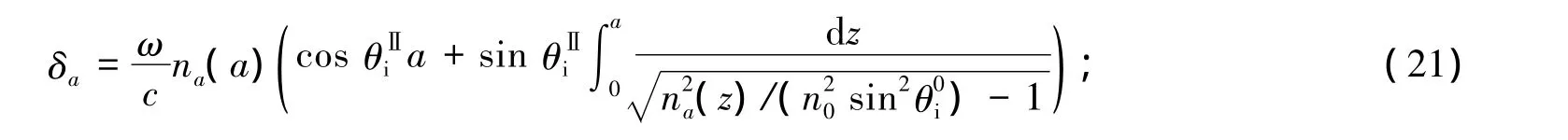
因此一个周期的传输矩阵为

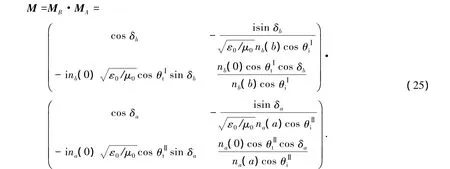
当nb(z)或na(z)为常数时，矩阵(25)即与常规光子晶体M矩阵相同，即常规光子晶体是一般函数光子晶体的特例.从而一般函数型光子晶体的特征方程为

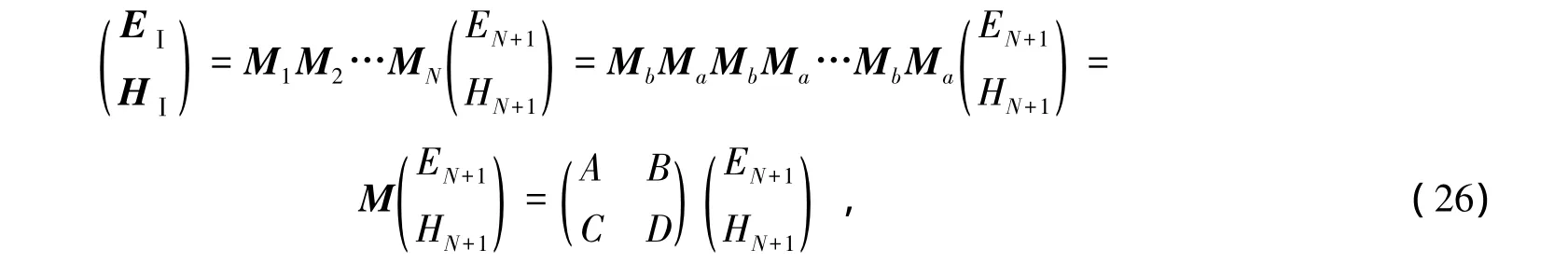
其中N为周期数.

由方程(26)可得透射系数t为

透射率为

光在一般函数光子晶体中的场强分布如图4所示.由一维函数光子晶体的传输矩阵可得光在光子晶体中的电场分布为

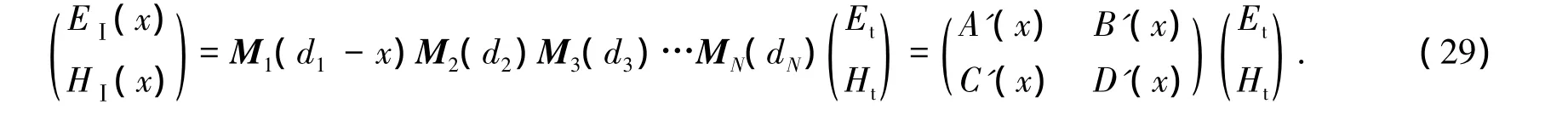
由方程(29)可得

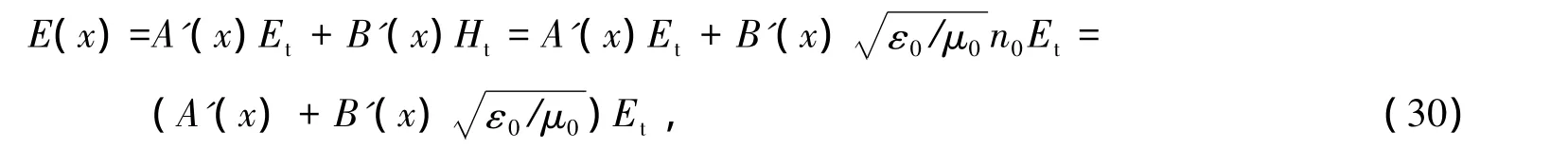
其中n0=1.由Et=E0i·t可得

比值为

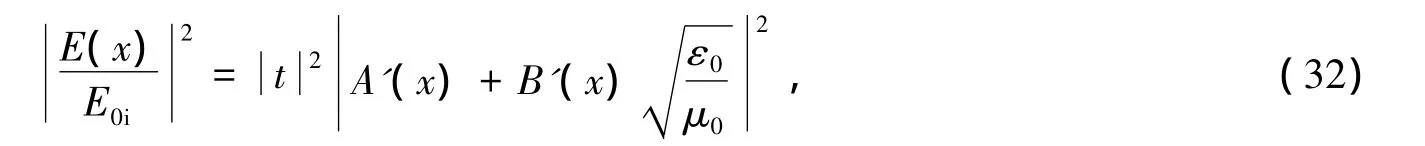
方程(32)即为一维函数光子晶体的电场分布公式.

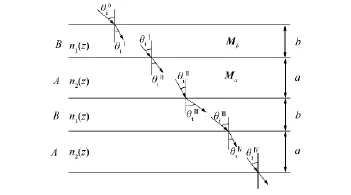
图3 光在一般函数光子晶体中2个周期内的传播路径Fig.3 Two-period transmission of light in the general function PCs

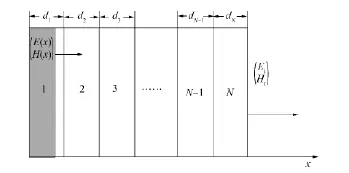
图4 光在一般函数光子晶体中的场强分布Fig.4 Light positive incident to the general function PCs

4 数值分析

折射率为空间坐标线性函数光子晶体的折射率分布函数为:

其折射率随位置的分布曲线如图5所示.给出端点值nb(0)，nb(b)，na(0)和na(a)即可确定线性函数折射率nb(z)和na(z).

采用图5所示的折射率线性分布函数:

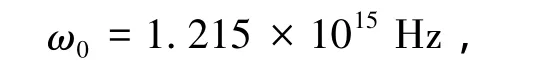
图5 一般函数光子晶体折射率随位置的分布曲线Fig.5 Enhanced line refractive indexes of function PCs in a period

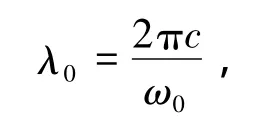
介质层B和A的厚度分别为

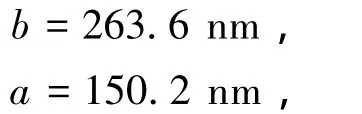
周期数N=16.通过计算可得一般函数光子晶体的透射率曲线如图6所示.由图6可见，一般函数光子晶体远大于常规光子晶体的透射率.

取

由方程(25)和(27)计算得到透射率曲线如图7所示.由图7可见，与常规光子晶体透射率相同.即常规光子晶体是函数光子晶体的特例.

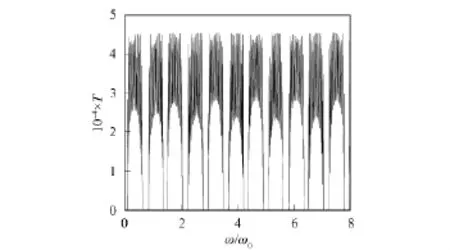
图6 一般函数光子晶体的透射曲线Fig.6 Transmissivity of function PCs

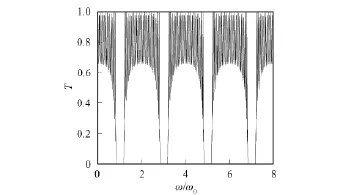
图7 常规光子晶体的透射率曲线Fig.7 Transmissivity of conventional PCs

光正入射和反入射进入函数光子晶体的电场分布曲线分别如图8和图9所示.由图8可见，当光正入射时，电场强度增强，实现了光放大.由图9可见，当光反入射时，电场强度减弱，实现了光衰减.因此该函数光子晶体可作为光子二极管.

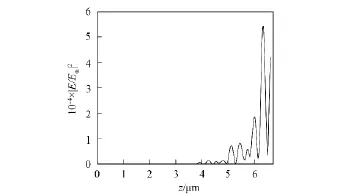
图8 光正入射进入一般函数光子晶体的电场分布曲线Fig.8 Light positive incident to the general function PCs

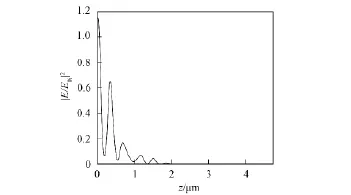
图9 光反入射进入函数光子晶体的电场分布曲线Fig.9 Light negative incident to the general function PCs

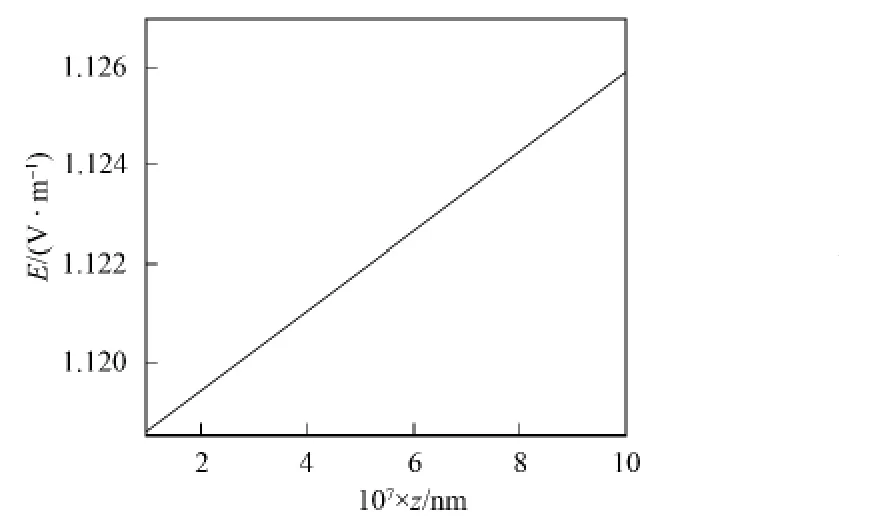
图10 电场在非均匀介质中的分布曲线Fig.10 Distribution of electric field in an inhomogeneous medium

5 电磁波在非均匀介质中的传播

由于非均匀介质的介电常数是随空间位置变化

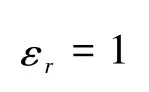
即该介质的折射率随空间距离增大而增大.根据电磁理论式［13］为

通过模拟计算得电场在非均匀介质中的分布曲线，如图10所示.由图10可见，电磁波在该非均匀介质中电场强度增加，这是因为电磁波在该非均匀介质的传播过程中吸收了能量，从而使电场强度增加.因此由该非均匀介质构成光子晶体时，其电场强度在每个周期都会增加.与函数光子晶体所得结果相符.

综上，本文设计了一种新型的线性函数光子晶体，其折射率为空间位置函数.通过计算得到如下结论:

1)当介质层B和A的折射率分布函数为线性增加时，一般函数光子晶体的透射率远大于1;

2)当光正入射时，电场强度增强，实现了光放大;当光反入射时，电场强度减弱，实现了光衰减.因此该函数光子晶体可作为光子二极管.

［1］Yablonovitch E.Inhibited Spontaneous Emission in Solid-State Physics and Electronics［J］.Phys Rev Lett，1987，58(20):2059-2062.

［2］John S.Strong Localization Photons in Certain Disordered Dielectric Super Lattices［J］.Phys Rev Lett，1987，58(23):2486-2489.

［3］WANG Hui，LI Yong-ping.An Eigen Matrix Method for Obtaining the Band Structure of Photonic Crystals［J］.Acta Physica Sinica，2001，50(11):2172-2178.(王辉，李永平.用特征矩阵法计算光子晶体的带隙结构［J］.物理学报，2001，50(11):2172-2178.)

［4］NI Pei-gen.Progress in the Fabrication and Application of Photonic Crystals［J］.Acta Physica Sinica，2010，59(1):340-350.(倪培根.光子晶体制备技术和应用研究进展［J］.物理学报，2010，59(1):340-350.)

［5］WANG Xu-dong，YAN Ke-zhu，LIU Fang.Study of Relations between Band Gap of Photonic Crystals and the Ratio of Dielectric Index［J］.Journal of Optoelectronics·Laser，2003，14(10):1063-1065.(王旭东，闫珂柱，刘芳.光子晶体带隙随介质折射率变化规律的研究［J］.光电子·激光，2003，14(10):1063-1065.)

［6］CHEN Wei-zong，SHEN Ying，HU Man-li，et al.Structure of Basic Period of One-Dimensional Photonic Crystal and the Characters of Forbidden Bands［J］.Acta Photonica Sinica，2001，30(12):1453-1456.(陈慰宗，申影，忽满利，等.一维光子晶体的基本周期结构及其禁带特征［J］.光子学报，2001，30(12):1453-1456.)

［7］Scalora M，Dowling J P，Bowden C M，et al.The Photonic Band Edge Optical Diode［J］.J Appl Phys，1994，76(4):2023-2026.

［8］John S，WANG Jian.Quantum Electrodynamics near a Photonic Band Gap:Photon Bound States and Dressed Atoms［J］.Phys Rev Lett，1990，64(20):2418-2421.

［9］John S，WANG Jian.Quantum Optics of Localized Light in a Photonic Band Gap［J］.Phys Rev B，1991，43(16):12772-12789.

［10］FANG Shu-fen，LI Ji-si，SU Shi，et al.Band Gap Properties of 1-D Photonic Crystal［J］.Journal of Jilin University:Science Edition，2009，47(1):98-101.(房淑芬，李集思，苏适，等.一维光子晶体的禁带特性［J］.吉林大学学报:理学版，2009，47(1):98-101.)

［11］Fink Y，Winn J N，Fan S，et al.A Dielectric Omnidirectional Reflector［J］.Science，1998，282:1679-1682.

［12］WANG Guang-huai，WANG Qing-cai，WU Xiang-yao，et al.Research on One-Dimensional Function Photonic Crystals［J］.Acta Physica Sinica，2012，61(13):134208.(王光怀，王清才，吴向尧，等.一维函数光子晶体的研究［J］.物理学报，2012，61(13):134208.)

［13］蔡圣善，朱耘，徐建军.电动力学［M］.2版.北京:高等教育出版社，2004:194-197.