一种基于改进Snake模型的边界检测方法

燕 杨，李岩波，王云吉，黄文博

(1.长春师范大学计算机科学与技术学院，长春130032;2.吉林大学通信工程学院，长春130012;3.吉林大学数学学院，长春130012)

图像分割是计算机视觉处理中的重要环节，每种图像分割模型都有其自身的特点和应用范围，在分割模型的选择上要根据所要分割目标图像的特点而确定，能够有效承载上层知识并融合底层特征的模型最具实用性和可行性［1］.在图像分割模型中，Kass等［2］提出的Snake模型是比较经典的模型，可以准确有效地将上层知识和底层特征相结合，即将图像数据所构成的外能和曲线梯度及曲率所决定的内能相融合分割图像.

目前，Snake模型的衍生模型较多，其中应用较广泛的是气球Snake模型和梯度向量流(GVF)Snake模型.如文献［3］在原始Snake模型中添加了一个气球力使得Snake演化曲线膨胀或收缩，扩大了曲线捕捉范围，克服了原始Snake模型对初始曲线位置的敏感问题，较准确地检测到了医学图像中的心室边界;文献［4-6］在梯度向量场(GVF)的基础上添加了一个新的主动轮廓外力，解决了原始Snake模型无法获取深凹边界及边界衔接不畅的问题.

本文针对原始Snake模型难以捕获深度凹陷边界的问题，提出一种新方法，即在原始外力基础上引入权值ω，使其与图像梯度大小成正比，从而自动调整外力大小，使演化曲线在加权外力的作用下能够进入到目标深度凹陷的区域.

1 原始Snake模型原理

原始Snake模型的基本思想是通过能量最小化，将一条初始曲线向待检测的目标轮廓方向逐步变形与运动，将一条带有能量函数的参数化曲线初始化在待分割目标周围，模拟物理上的力学原理，在内力(控制曲线的弯曲和拉伸)和外力(主要为图像力)作用下，利用能量最小化作为框架，不断地演化变形，最终收敛到目标边界，得到一个光滑且连续的轮廓［7-8］.构造Snake模型的能量函数定义为

其中:V(s)表示待分割目标的外轮廓;s∈［0，1］为归一化的弧长参数;Eint表示轮廓的内部能量，即模拟物理学上的内力，用于度量轮廓的光滑性和弹性.

内能Eint是由Snake模型演化曲线形状的基本属性决定的，表示为

其中Vs表示曲线对参数s的一阶微分，是弹性能量项，表示曲线的长度变化率，控制演化曲线的收缩程度;Vss表示曲线对参数s的二阶微分，是刚性能量项，表示曲率向量，控制曲线沿法线方向朝目标演化的速度;α表示弹力系数，控制曲线收缩速度的快慢;β表示强度系数，控制曲线的弯曲程度，取值越大，表示轮廓曲线越僵硬，不容易弯曲，越小则反之.

外能Eext表示为

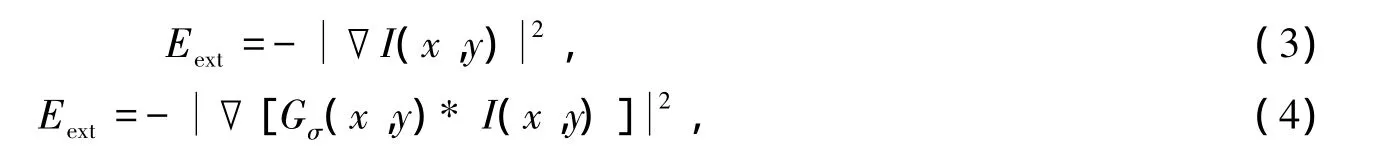
其中:Eext表示外部能量，即外力，代表图像的信息在轮廓曲线演化的过程中偏向图像梯度值较大的位置;▽表示梯度算子;*表示卷积;I(x，y)表示图像的灰度值;Gσ(x，y)表示方差为σ的高斯滤波器.式(3)直接对图像求取梯度，式(4)先用二维高斯滤波器对图像进行滤波，滤掉高频噪声的干扰，然后再求梯度.两种方法相比较，将式(4)作为外力时分割效果更好.因此，由式(1)，(2)，(4)可得

采用有限差分法求能量最小化，即最小化式(5)，其过程如下:式(5)满足Euler-Lagrange方程

即

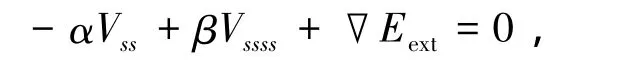
可视为一个力平衡方程式:

所以求解方程即能量最小化可视为Snake模型的演化曲线在内外两力的共同作用下，达到平衡状态，此时的能量值最小.

演化曲线随时间不断变化，引入t作为时间变量，此时演化曲线是动态函数E(s，t)，则求演化曲线的偏微分方程转化为

将式(8)离散化得

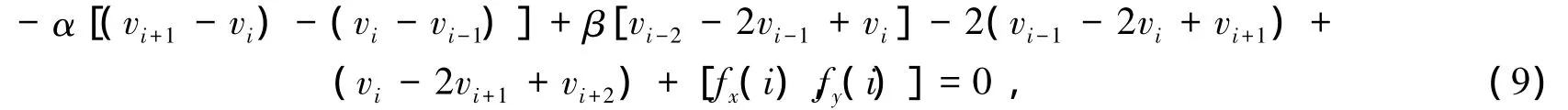
通过为式(9)赋一个初始值以得到初始轮廓，然后不断迭代，直到收敛.曲线越趋于边缘，曲线的演化程度越不明显，梯度越大，曲线长度的变化率越小，能量也越小，当能量达到极小值时，即内外力平衡时，此时曲线即为轮廓.在相同的迭代步数下，α越大，曲线的收缩速度越快，每步演化的收缩幅度也越大.由于原始Snake模型使用图像灰度梯度作为外力的限制，所以无论迭代多少次，演化曲线始终难以捕获目标深度凹陷的边界.

2 改进的Snake模型

为解决原始Snake模型在深度凹陷边界检测中存在的问题，本文在Snake模型原始外力的基础上引入一个自动控制外力大小的权值ω，则外力Fext由下式给出:

其中

式(10)中，ω为控制图像外力大小的权值，与图像梯度成正比，其值的选取自动进行，无需人工干预.式(11)中，m为实数且m＞0，▽2f为Laplace算子，在像素变化缓慢的区域，ω=0，即像素点f(x，y)的梯度为0.在ω值较大的位置，曲线收缩或膨胀的程度也大，增加了能量场的作用范围，使演化曲线在加权外力作用下能进入到目标深度凹陷的区域，从而更容易捕获到目标深度凹陷的边界，其求解过程与原始Snake模型相同.

在OpenCV中，实现这种加权Snake模型，本文给出两组实验结果.

图1为人工合成图像的边界检测结果，参数分别为:α=0.45，β=0.005，σ=0.2，权值ω=1.0，其中图1(A)是初始轮廓，图1(B)是原始Snake模型对人工合成图像边界检测的结果.由图1(B)可见，演化曲线最终停留在深度凹陷区域的入口无法进入.图1(C)是本文改进Snake模型的边界检测结果.由图1(C)可见，在加权外力的作用下，演化曲线进入了目标凹陷区域，很好地捕获到了目标深度凹陷的边界.

图1 改进Snake模型对人工合成图像进行边界检测的结果Fig.1 Boundary detection result of the synthetic image

图2为对脑转移瘤核磁共振图像进行分割的结果.由于不规则形状的阴影部分存在狭窄的凹陷区域，原始Snake模型很难进入，而在改进的Snake模型加权外力作用下，演化曲线较好地捕获了凹陷区域的边界，得到了较理想的实验结果.因此，加权Snake模型改善了原始Snake模型无法捕获凹陷边界的缺陷，能较好地收敛到目标深度凹陷的边界，同时收敛速度也较原始Snake模型有所提高.

综上，本文在对原始Snake模型进行深入分析和实验的基础上，针对其不足提出了一种改进的算法:在原始Snake模型外力的基础上引入一个自动控制外力大小的权值，令其与图像梯度大小成正比，使曲线可继续向内收缩或向外膨胀，演化到能量场的有效作用范围内，最终收敛到目标轮廓;利用Laplace扩散方程处理Snake模型的图像力，将梯度信息扩展到更远的均匀区域，扩大了Snake演化曲线的搜索范围，从而实现演化曲线收敛到目标深度凹陷边界的效果.

图2 改进Snake模型对脑部MR图像边界检测的结果Fig.2 Boundary detection result of the brain MR image

［1］LI Qing，YANG Jun-feng，JIANG Han-hong，et al.A Segmentation Method Based on Snake Model［J］.Journal of Wuhan University of Technology:Information＆Management Engineering，2006，28(11):168-171.(李庆，杨俊峰，江汉红，等.基于Snake模型的图像分割技术［J］.武汉理工大学学报:信息与管理工程版，2006，28(11):168-171.)

［2］Kass M，Witkin A，Terzopoilos D.Snakes:Active Contour Models［J］.Int J Comput Vis，1987，1(4):321-331.

［3］Cohen L D.On Active Contour Models and Balloons［J］.CVGIP:Image Understanding，1991，53(2):211-218.

［4］XU Chen-yang，Prince J L.Snakes，Shapes，and Gradient Vector Flow［J］.IEEE Transactions on Image Processing，1998，7(3):359-369.

［5］XU Chen-yang，Prince J L.Gradient Vector Flow:A New External Force for Snakes［C］//Proceedings of the 1997 Conference on Computer Vision and Pattern Recognition.Washington:IEEE Computer Society，1997:66-71.

［6］Prince J L，XU Chen-yang.A New External Force Model for Snakes［C］//Proceedings of the Image and Multidimensional Signal Processing Workshop.London:［s.n.］，1996:30-31.

［7］WANG Pei.Research on Technique of Medical Image Segmentation Based on Active Contours Model［D］.Harbin:Harbin Institute of Technology，2010.(王佩.基于活动轮廓模型的医学图像分割技术研究［D］.哈尔滨:哈尔滨工业大学，2010.)

［8］JIAN Jiang-tao.Deformation Model Technology and Its Application in Medical Image Segmentation［D］.Hefei:University of Science and Technology of China，2007.(简江涛.形变模型技术研究及其在医学图像分割中的应用［D］.合肥:中国科学技术大学，2007.)