一类带单洞区域与两个简单区域间拓扑关系的表示

李 健，廖梦兰，温长吉

(吉林农业大学信息技术学院，长春130118)

空间推理［1-2］在地理信息系统(GIS)［3］、图像数据库、模式识别、机器人导航、高级视觉、自然语言理解、工程设计、物理位置的常识推理、空间数据库［4］等方面应用广泛.目前，人们已提出了一些基本模型，如9-交模型［5］、D9-交集模型［6］、区域连接演算［7］和区域间拓扑关系的层次表达法［8］等，这些模型主要用于描述两个区域间的拓扑关系，即仅包含简单区域或仅包含非简单区域，而对于多个区域间(即同时包含简单区域与非简单区域)拓扑关系的研究较少，但实际应用中很多时候需要同时考虑多个区域间的相互关系，因而建立适用于多个区域间拓扑关系的模型十分必要.

本文建立了带单洞区域与两个简单区域间拓扑关系的表示模型，基于RCC5定义了扩展4-交矩阵，进而给出12-交集模型，并给出了带单洞区域与两个简单区域间的161种拓扑关系图和概念邻域图.

1 扩展4-交集矩阵、12-交集模型及带单洞区域与两个简单区域间的约束条件

1.1 扩展4-交集矩阵

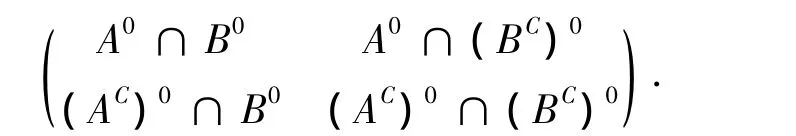
通过考察扩展4-交集矩阵中每个位置集合的空与非空描述RCC5关系，RCC5关系集的矩阵表示列于表1.

表1 RCC5关系集的矩阵表示Table 1 Matrix representation of RCC5 relations

1.2 12-交集模型

扩展4-交集矩阵只能表示两个区域间的拓扑关系，对两个以上区域间的拓扑关系无法表示.为此，基于扩展4-交集模型，本文给出了可以对带单洞区域与两个简单区域间拓扑关系进行表示的12-交集模型.

定义1 取圆A内部一个圆B，将圆B称为圆A的洞，如图1所示.

定义2 若有区域A包含简单区域B，即满足RCC5关系集中的PPI(A，B)，同时简单区域C与简单区域D相离，即满足RCC5关系集中的DR(C，D)，则称区域A，B，C，D共同构成一类带单洞区域与两简单区域，如图2所示.

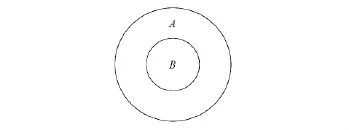
图1 一个简单的带洞区域Fig.1 A simple region with a hole

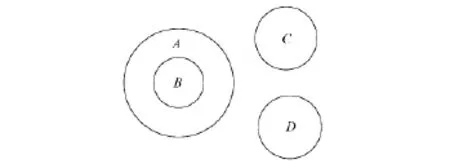
图2 带单洞区域与两简单区域Fig.2 A simple region with a hole and two simple regions

对扩展4-交集矩阵进行进一步扩展，可得到16-交集模型［9］.对16-交集模型进行研究表明，在16-交集矩阵中有些位置的元素是确定的.对于本文的带单洞区域与两简单区域，区域A与区域B的拓扑关系为PPI(A，B)，即如下等式成立:

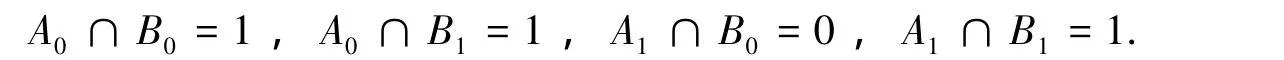
由于A1∩B0=0，所以其再与其他的任一部分取交集，其结果也必然为0，因此在16-交集矩阵中如下等式确定:

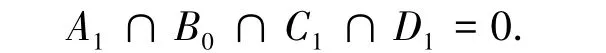
因此，无论简单区域C和简单区域D的位置如何变动，区域A和区域B间的拓扑关系不影响区分模型表示.

根据上述分析，可将16-交集模型进行改进，进而得到如下12-交集矩阵:

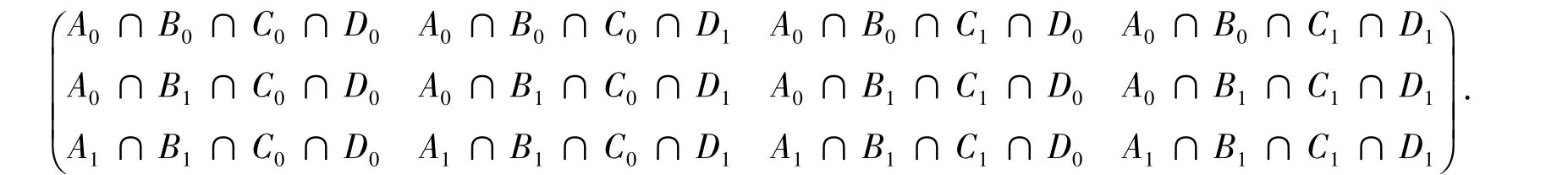
对于任意的带单洞区域与两个简单区域，本文可用上述12-交集矩阵表示它们之间的拓扑关系，即每个12-交集矩阵都对应一个A，B，C，D之间的拓扑关系，如图3所示.

1.3 带单洞区域与两个简单区域间的约束条件

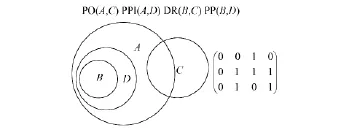
图3 对应实例Fig.3 Corresponding example

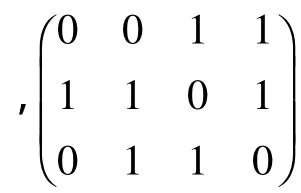
为了得到所有可实现的12-交集矩阵，本文对带单洞区域与两个简单区域进行进一步研究，给出如下3个约束条件.

约束条件1 一个12-交集矩阵能对应一个可实现的6组拓扑关系，必须满足所有的两两关系属于RCC5关系集.

约束条件2 对于简单区域有界区域，必须满足A1∩B1∩C1∩D1非空，即M1111=1.

约束条件3 由于带单洞区域与两个简单区域间的4个部分A，B，C，D，有简单区域C与简单区域D相离，所以可得如下表达式:

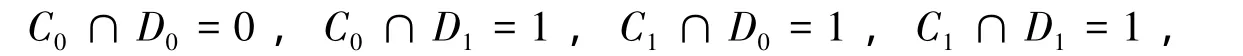
即0-1矩阵应满足:

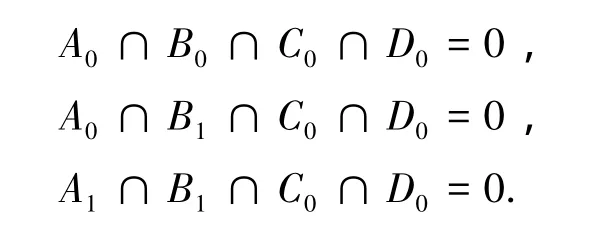
2 带单洞区域与两个简单区域间拓扑关系的算法及表示

算法的基本思想如下:

1)每个12-交集矩阵以(a1，a2，…，a12)的行向量形式给出，先生成理论上的212种12-交集矩阵，即生成一个由212个行向量构成的矩阵A;

2)依次扫描A的每行，标记矩阵A中所有满足约束条件的行向量;

3)将矩阵A中所有满足条件的行向量保存到矩阵B中，并输出，其结果即为所求.

根据该算法，可得到161种12-交集矩阵，经验证这161个12-交集矩阵都能唯一对应一个可实现的带单洞区域与两个简单区域间的拓扑关系，这161种拓扑关系如图4所示.

定理1 所有由12-交集模型给出的带单洞区域与两个简单区域间可实现的161种拓扑关系是两两互斥且完备的.

证明:因为由12-交集模型给出的带单洞区域与两个简单区域间的212种拓扑关系(包括可实现的和不可实现的)是两两互斥且完备的，所以只需说明其中可实现的拓扑关系有且仅有161种.约束条件1和约束条件2是拓扑关系可实现的必要条件，通过这两个约束可得到161种可能实现的拓扑关系，而图4表明可以对这161种拓扑关系找到相应的具体情形实现，因此单洞区域与两个简单区域间可实现的拓扑关系有161种，而且是两两互斥且完备的.

图4 161种可实现的拓扑关系Fig.4 161 topological relations and their schematics

综上所述，本文基于RCC5，定义了扩展4-交集矩阵，进而给出12-交集模型，对带单洞区域与两个简单区域间的拓扑关系进行了表示，并给出了带单洞区域与两个简单区域间161种拓扑关系的示意图.

［1］WANG Sheng-sheng，LIU Da-you.Knowledge Representation and Reasoning for Qualitative Spatial Change［J］.Knowledge-Based Systems，2012，30:161-171.

［2］WANG Sheng-sheng，LIU Da-you.An Efficient Method for Calculating Qualitative Spatial Relations［J］.Chinese Journal of Electronics，2009，18(1):42-46.

［3］Scott J，Lee L H，Arends J，et al.Designing the Low-Power M*CORE Architecture［C］//IEEE Power Driven Microarchitecture Workshop.Haifa，Israel:IEEE Computer Society，1998:29-33.

［4］LI San-jiang，YING Ming-sheng.Region Connection Calculus:Its Models and Composition Table［J］.Artif Intell，2003，145(1/2):121-146.

［5］CHANG Ning-san，FU King-sun.Query by Pictorial Example［C］//IEEE Transactions on Software Engineering.Piscataway:IEEE Press，1980:519-524.

［6］OUYANG Ji-hong，HUO Lin-lin，LIU Da-you，et al.Extended 9-Intersection Model for Description of Topological Relations between Regions with Holes［J］.Journal of Jilin University:Engineering and Technology Edition，2009，39(6):1595-1600.(欧阳继红，霍琳琳，刘大有，等.能表达带洞区域拓扑关系的扩展9-交集模型［J］.吉林大学学报:工学版，2009，39(6):1595-1600.)

［7］GUO Luo，DU Shi-hong，WANG Qiao.Deriving Topological Relations between Uncertain Regions from Direction Relations［J］.Acta Scientiarum Naturalium Universitatis Pekinensis，2009，45(2):339-349.(郭泺，杜世宏，王桥.基于方向关系的不确定区域拓扑关系推理［J］.北京大学学报:自然科学版，2009，45(2):339-349.)

［8］Clarke B L.A Calculus of Individuals Based on“Connection”［J］.Notre Dame Journal of Formal Logic，1981，22(3):204-218.

［9］LI Jian，OUYANG Ji-hong，WANG Zhen-xin.Representation for Topological Relations of Four Simple Regions［C］//The 2012 9th International Conference on Fuzzy Systems and Knowledge Discovery(FSKD’12).Piscataway:IEEE Press，2012:2961-2965.