第二类Siegel域到超球上一个双全纯双射变换

朱小林，贺君燕

(1．上海海事大学 文理学院，上海201306;2．上海电力学院 数理系，200090)

1 问题提出

当 n≥2 时，文［1］［2］给出了一个 Dn={(w，u1，…，un－1)∈Cn|2Im w － u u—T＞0}到超球 Bn={z=(z1，…，zn)∈Cn|1－z z—T=1－|z1|2－…－|zn|2＞0}的一个双全纯双射变换T:

令t为T:Dn→Bn的变换矩阵，由(1)得，从而 Aut(Dn)=t－1Aut(Bn)t．自同构群的算术子群在数论中是有意义的，如:现代数论的中心领域之一的自守形式就是定义在算术子群上的．复矩阵t给出了自同构群的关系，然而相对应的算术子群的关系其数论性质就变复杂了，原因就在于矩阵t中出现了无理数，本文作者将研究能不能找到一个合适的双全纯双射变换A，使相对应的算术子群能保持良好的算术性质．

令:In，1=，其中In表n阶单位矩阵．则由［3］:

进而有:

当n=1时，式(2)、(3)分别为复单位圆盘和复上半平面自同构群，此时

由以上关系，关键寻找变换矩阵An+1，满足Aut(Dn)=A－1n+1SU(n，1)An+1，An+1具有良好的算术性质．作者将寻找由高斯整数构成的模矩阵An+1(以下简称模矩阵:即逆矩阵仍为高斯整数构成，也即为行列式的模为1的矩阵)．对应的双全纯双射变换Α:Dn→Bn，称为模变换．

2 模矩阵的条件

引理1 当n≥1时，若存在An+1满足

证明 ∀s∈SU(n，1)，则令:g=A－1n+1sAn+1，有:

证毕．

命题1 不存在模变换将单位开圆盘映射成复上半平面．

由以上命题，以下n≥2．

再令:Γn+1=Aut(Dn)∩SL(n+1，Z［i］)，则有:

定理1 Mn+1=An+1Γn+1，其中 An+1∈Μn+1．

证明 ∀Υ∈Γn+1，令A=An+1Υ，有:

所以有:An+1Γn+1⊆Mn+1．

反过来:A，B∈Mn+1，易得 BA－1∈Γn+1;即:Mn+1⊆An+1Γn+1．证毕．

由上定理1可知关键是找出一个模矩阵An+1，因为所有满足条件的模矩阵相差Γn+1中的一个元素．

3 模矩阵计算

引理 2 存在模矩阵 A3，满足 A—T3I2，1A3= － H1，1．

证明 令:A3=SL(3，Z［i］)，由:A—T3H1，2A3= － I2，1，得:

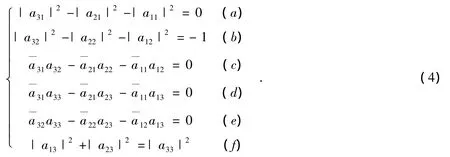
由 aij为高斯整数，由式(4)中(a)和(f)得:|a31|≠0，|a33|≠0，取|a31|=|a33|=1(模最小)，即:a31=in，a33=im(n，m∈Ζ)．由式(a)和(f)继续令:a21=a13=0，a11=ip，a23=iq得:

条件方程组(4)化为:

由以上方程组令:m=q=p=s=4得:

满足引理要求．证毕．

引理3 n≥2时，存在模矩阵 An+1，满足

证明 n=2，即引理2，下证:n＞2引理成立．令:

则直接计算得:

证毕．

4 问题的解答及应用

进一步得:

即Α0是Dn到Bn一个双全纯双射的变换矩阵．

定理2 当n≥2时，若An+1∈SL(n+1，Z［i］)且为Dn→Bn一个双全纯双射的一个变换矩阵，则:

证明 由引理1得证必要性．下证充分性:

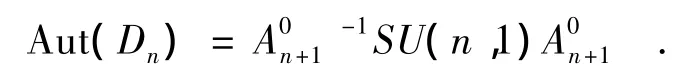
证毕．

［1］朱小林，陆洪文．椭圆元在维数公式中的贡献［J］．数学年刊(A辑)，2007，28(2):281．

［2］朱小林，陆洪文．第二类Siegel域上自同构群Iwasawa分解的Haar测度显式［J］．同济大学学报:自然科学版，2007，35(7):980．

［3］华罗庚．多复变数函数论中的典型域的调和分析［M］．2版．北京:科学出版社，1965．

［4］GOMELIN T W．Complex Analysis［M］．北京:世界图书出版公司北京公司，2008．