一种修正的DY共轭梯度法的全局收敛性

敖 卫 斌

(重庆师范大学 数学学院，重庆 401331)

一种修正的DY共轭梯度法的全局收敛性

敖 卫 斌

(重庆师范大学 数学学院，重庆 401331)

提出了一种新的非线性修正的DY共轭梯度算法(MDYCG),该算法得到的搜索方向为下降方向，它既不受线搜索规则的影响；也不受目标函数的凸性影响；在精确线搜索下，MDYCG算法化归为标准的DY共轭梯度算法；证明了该方法在Armijo型线搜索下的全局收敛性，给出了初步的数值结果。

无约束优化；共轭梯度法；Armijo型线搜索；全局收敛性

0 引 言

考虑无约束优化问题：

minf(x),x∈Rn

(1)

其中f：Rn→R为连续可微函数，其梯度向量记为g(x)，简记为g。

共轭梯度法是求解大规模无约束优化问题的有效算法之一，它像最速下降法一样在每步迭代中不需要存储和计算矩阵，其迭代格式：

xk+1=xk+αkdk

(2)

(3)

其中，gk=f(xk)，dk为搜索方向，αk是通过一维线搜索获得的步长，βk为标量。不同的βk对应着不同的共轭梯度算法。1964年, Fletcher和Reeves首先提出非线性共轭梯度法参数βk，它定义为还有其他著名的βk，比如：

其中‖·‖为欧几里得范数,yk-1=gk-gk-1。FR方法、CD方法和DY方法具有较好的理论收敛性，然而PRP方法、HS方法和LS方法具有较好的数值计算结果。

在文献[9]的启发下，选取不同的βk，提出了一种修正的DY算法(MDYCG)并证明了该算法在Armijo型线搜索下的全局收敛性。所采用的Armijo型线搜索准则，取步αk：

αk=max{ρj,j=0,1,2,…}

(4)

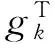
(5)

其中ρ∈(0,1),δ1∈(0,1),δ2>0。

2 修正的DY新算法

本文给出的新算法迭代式(2)和式(6)：

(6)

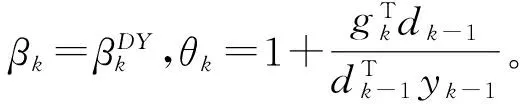
(7)

下面给出新的算法步骤：

(1) 给出x1∈Rn，ρ∈(0,1),δ1∈(0,1),δ2∈(0,1),ε≥0，令k：=1,d1=-g1，若‖g1‖≤ε，立即停止；

(2) 找到αk>0满足Armijo型线搜索规则；

(3) 令xk+1=xk+αkdk, 且gk+1=g(xk+1)，若‖gk‖≤ε，立即停止；

(5) 令k=k+1，返回(2)。

本文做如下假设：

(A)f(x)在水平集Ω={x∈Rn|f(x)≤f(x1)}有下界，其中x1为初始点;

(B)Ω的一个领域N内，f连续可微且其梯度向量满足Lipschitz条件，即存在常数L>0，使得:

‖g(x)-g(y)‖≤L‖x-y‖,∀x,y∈N

(8)

同时由上述的假设可以得到存在正常数β和γ满足：

‖x‖≤β, ‖g(x)‖≤γ,∀x∈Ω

(9)

3 算法的收敛性

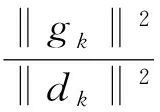
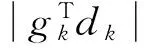
如果αk<1, 由Armijo型线搜索规则,ρ-1αk不满足式(5)。则有：

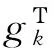
(10)

由中值定理和假设B，存在某一个tk∈(0,1)使得：

(11)

结合不等式(10)、式(11)和式(7)得：

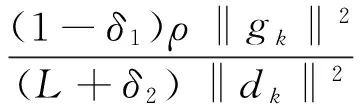
证毕。

引理2 假设(A)，(B)成立，MDYCG算法中αk满足Armijo型线搜索，则有Zoutendijk条件：

(12)

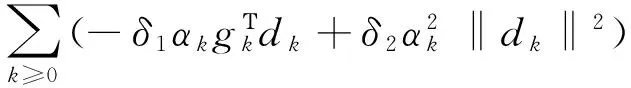
(13)

定理3 若假设(A)和(B)成立，MDYCG算法中αk满足Armijo型线搜索，或者对某个k成立，或者有：

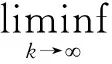
‖gk‖=0

证明反正法。假设结论不成立，则存在一个常数ε使得式(14)成立，式(14)如下：

‖gk‖≥ε，∀k≥0

(14)

4 数值试验

本节在标准Armijo型非精确线搜索准则下，利用MARTLAB 7.1， MDY方法对测试函数[10]进行试算。表格中Problem表示测试函数的名称,NI/NF/NG分别代表迭代次数、函数迭代次数、梯度迭代次数，Dim表示测试函数自变量的个数，“—”表示迭代失败。计算中参数σ=0.5，ρ=0.8，取ε=10-5，VP代表极值点，OV代表极值。终止条件为‖gk‖≤10-5。表1简单的数值试验表明了新方法的特点，该方法是有效的。

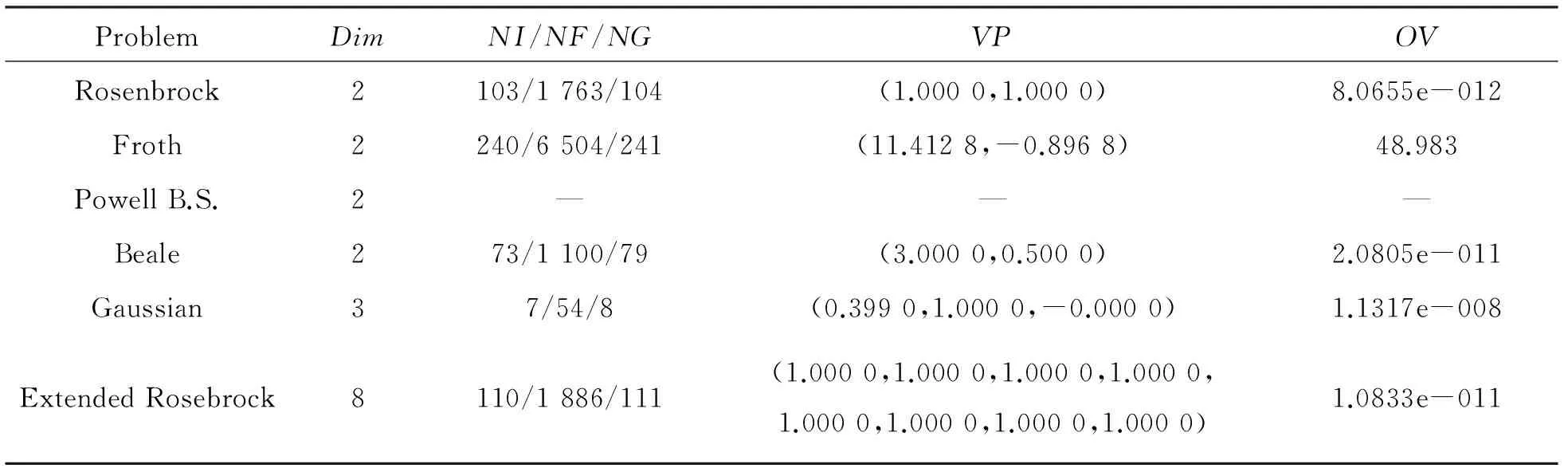
表1 MDY方法在Armijo型搜索下的数值结果

[1] SHI Z J. Convergence of line search methods for unconstrained optimization [J]. Applied Mathematics andComputation, 2004(157)：393-405

[2] FLETCHER R, REEVES C. Function minimization by conjugate gradients[J]. Computer Journal, 1964( 7)：149-154

[3] POLAK E ，RIBIERE G. Note sur la convergence de directions conjugees[J]. Rev Francaise InformatRecherche Operatinelle, 3e Annee, 1969(16)： 35-43

[4] POLAKB T. The conjugate gradient method in extremem problems[J]. USSR Comp Math and Math. Phys.1969(9)： 94-112

[5] HESTENES M R， STEIFEL E L. Methods of conjugate gradients for solving linear systems[J]. J Res Nat Bur Standards Sect. 1952, 5(49)： 409-436

[6] LIU Y， STIEFELC. Efficient generalized conjugate gradient algorithms[J].JOTA, 1991， 69(1)： 129-152

[7] DAI Y， YUAN Y. A nonlinear conjugate gradient with a strong global convergence property[J]. SIAM Journal on Optimization, 1999, 10(1)： 177-182

[8] FLETCHER R. Practical methods of optimization [M]. New York： Unconstrained Optimization,1987

[9] ZHANG L, ZHOU W.LI D. Global convergence of a modified Fletcher-Reeves conjugate gradientmethod method with Armijo-type line search[J]. Numerische Mathematik 2006,104(4)：561-572

[10] MORE J,GARBOW B,HILLSTROMK E. Testing unconstrained optimization software[J].ACM Trans,Math.Software,1981,7(1)：17-41

Global Convergence for a Modified DY Conjugate Gradient Algorithm

AOWei-bin

(School of Mathematics, Chongqing Normal University, Chongqing 401331, China)

This paper proposes a kind of new nonlinear modified DY conjugate gradient algorithm, whose search direction is descent direction and which is not affected by line search rule and is not affected by the convexity of objective function either.Under accurate line search, the modified DY conjugate gradient algorithm is turned to standard DY conjugate algorithm. This paper proves the global convergence of this algorithm under Armijo-type line search and gives initial numerical result.

unconstrained optimization；conjugate gradient algorithm；Armijo-type line search；global convergence

1672-058X(2013)10-0017-04

2013-04-07；

2013-05-07.

敖卫斌(1987-)，男，重庆九龙坡人，硕士研究生，从事最优化理论与研究.

O182.1

A

责任编辑：代小红