Rogowski线圈中积分环节的研究

朱 超 ，蒋 煜 ，梅 军 ，郑建勇

（1.东南大学 电气工程学院，江苏 南京 210096；2.苏州供电局，江苏 苏州 215000）

0 引言

随着电力工业的发展，电力传输系统容量不断增加，运行等级也越来越高，传统的电磁式互感器已难以满足需求。而以Rogowski线圈为传感头的电子式互感器，其测量线性度好，无饱和，测量频率范围宽，反应速度快，不存在磁饱和的问题，适用于测量变化速度快的大电流，可用于电力系统高压侧电流的检测、保护和控制，已成为电力系统的发展趋势［1-3］。

但由于Rogowski线圈的输出电压正比于被测电流对时间的微分，因此需要对输出电压进行积分，以还原出被测电流信号，所以积分环节对于电子式互感器是相当重要的。目前现场使用的多以惯性环节构成的模拟积分器为主。由于实际器件不是理想器件，运放的漂移、电容的泄漏与损耗等使得模拟积分器在长期运行时很可能出现随时间和外界环境温度进行的漂移现象。为了克服模拟积分器的缺陷，可以使用数字积分的方法［4-6］。数字积分器设计灵活，受环境干扰小，可靠性和可重复性高，避免了传统模拟积分器温漂、时漂的问题。

1 Rogowski线圈的传感原理

Rogowski线圈的等效电路图如图1所示，其中，R0为Rogowski线圈的内阻，L0为Rogowski线圈的自感系数，RL为负载电阻，C0为Rogowski线圈的匝间电容，e（t）为 Rogowski线圈的感应电势。

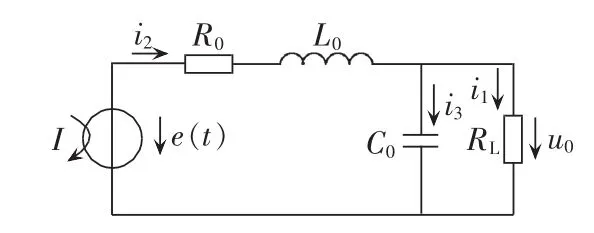
图1 Rogowski线圈等效电路图Fig.1 Equivalent circuit of Rogowski coil

进行基本电路分析，并作拉普拉斯变换可得：

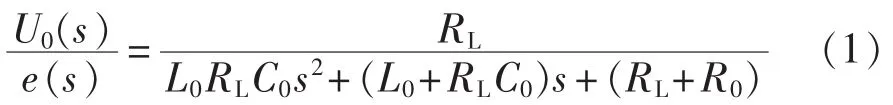
根据设计不同的参数，Rogowski线圈可分为内积分式和外积分式2种。当Lω≫RL+R0并且1/（Cω）≫RL时，负载电阻上的电压U0与被测电流的大小成正比关系，为内积分式空心线圈电流互感器；当 RL≫Lω+R0且 1/（Cω）≫R0+Lω 时，负载电阻上的电压U0与被测电流对时间的微分成正比关系，为外积分式空心线圈电流互感器，需要积分电路来还原被测电流。外积分式空心线圈电流互感器在电力系统中使用广泛，适用于中低频段。外积分电路分为有源型和无源型2种，应用较广的是信噪比较高、增益灵活可调的有源积分方式［7-8］。有源积分方式可用模拟积分和数字积分2种方式实现。

2 模拟积分器的原理

基于Rogowski线圈的电子式电流互感器，在传感环节，测得电压，根据电磁感应原理，测得电压相位理论上超前被测电流90°，在积分环节可以将相位还原，配合理想模拟积分器，则被测电流的相位不会产生畸变［9-10］。模拟积分器中使用的运算放大器只有在线性工作区内可以正常工作，存在饱和问题。为了抑制积分器的饱和，实际使用中在非理想积分器的积分电容C两端并联反馈电阻Rf，如图 2 所示。

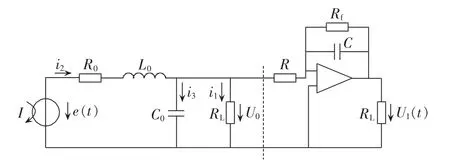
图2 电子式电流互感器等效电路与积分环节Fig.2 Equivalent circuit of electronic current transducer with integrator

这样由Rogowski线圈和带反馈通道的模拟积分器组成的系统联合系统传递函数为：

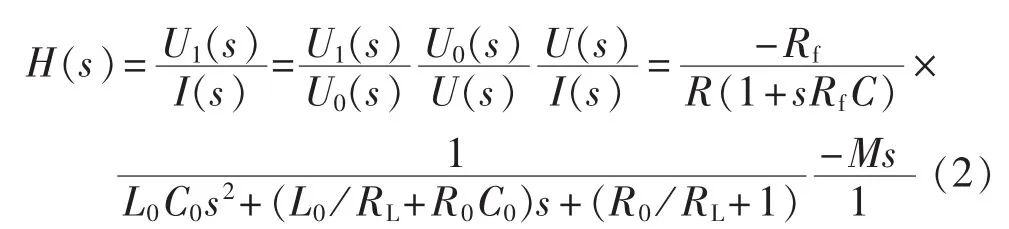
但是若积分器的反馈参数配置不当，其暂态输出波形将严重失真。适当地提高积分器的反馈电阻Rf值以及积分电容C可以改善其暂态传变特性。但在实际应用中，模拟积分器受到严重的稳定性困扰。实际物理器件存在失调电流、偏置电流和温度漂移等非理想因素的干扰，产生的直流量经过积分电容的累积，最终在输出端叠加在信号上输出。

完全理想的运算放大器在实际中是无法实现的，在实际中使用的运算放大器是指由IC构成的运算放大器，图3给出了其简化的等效电路。由图3可知，在考虑运算放大器的高频响应时，输入与输出波形的响应情况是不同的，对于阶跃响应，当输入振幅较小时，由于电容C和其他因素的影响会出现波浪形的滞后，输入振幅较大时，由于SR的影响会使输出产生直线状的滞后；对于正弦波的响应，在频率很高时，将会出现一定的相位滞后。

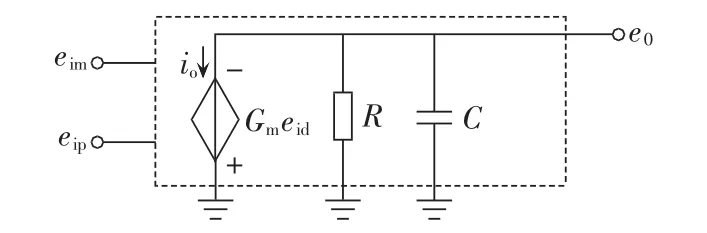
图3 IC运算放大器的等效电路Fig.3 Equivalent circuit of IC amplifier

此外，当有大振幅输入时，由于IC内部不会瞬间发生大电流，所以输出的变化需要时间，这种变化的快慢用转换速率来表征。转换速率指运算放大器的输出电压在单位时间内能够变化的电压量。由于转换速率的存在，运放的响应是有滞后的，这样高频的输入电压将与理论值不相等而产生误差。

采用IC运算放大器实现的模拟积分电路，在输入信号经过其中进行运算积分的过程中，由温度变化、电磁干扰等产生的电压漂移、器件本身产生的噪声等，都是无用信号，作为误差计入，但由于模拟积分电路的放大效应，微小误差经过负反馈加入输入端信号中多次循环放大，最终对测量结果造成极大的干扰，甚至会淹没有用信号，对后期测量和保护动作造成极大不利，这也是电子式电流互感器应用中需要解决的一大问题［11-12］。

3 数字积分器的原理

同模拟积分器相比，数字积分器具有较多优点，如结构简单，受温漂、时漂的影响较小，性能稳定，相位特性优良，结构灵活，调节方便等。利用软件和芯片编程即可简便地实现数字积分功能，便于调试和检测。

常见的数字积分算法主要有复化矩形算法、梯形算法、Simpson 算法等［13-14］。设 Ts为采样间隔，以上3种积分算法的z传递函数HR、HT和HS分别为：

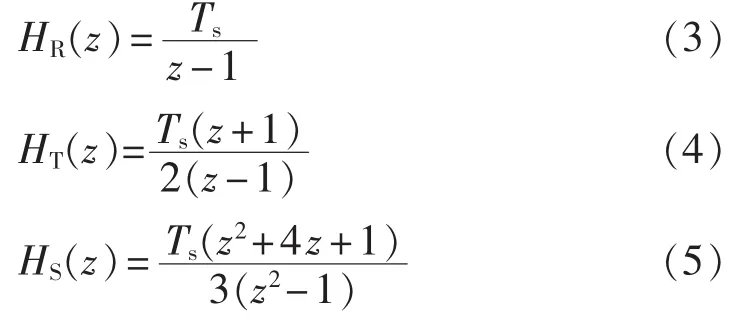
由z域传递函数可以看出存在极点z=1，由于z=ejω，即 ω=0 时，出现极值，若存在直流分量，积分值将会不稳定，直流分量将会被无限放大。

因此若采用简单的数字积分算法进行积分，由于数据字长有限为16位，经过几个周期之后就很快溢出了。因为AD的前端电路对信号进行抗混叠滤波等信号处理时，将不可避免地引入直流分量［15］。用传统的数字积分方法积分，积分值就会随着运行时间而不断偏移，最终超出寄存器所能表示的数值范围而溢出。

4 数字积分器的实现

4.1 数字积分器的设计

为了减小输入的低频分量带来的影响，可参考低频增益平坦模拟积分器进行数字积分器的设计，该积分器对于低频分量有很好的抑制作用，积分器的电路图如图 4 所示［16］。

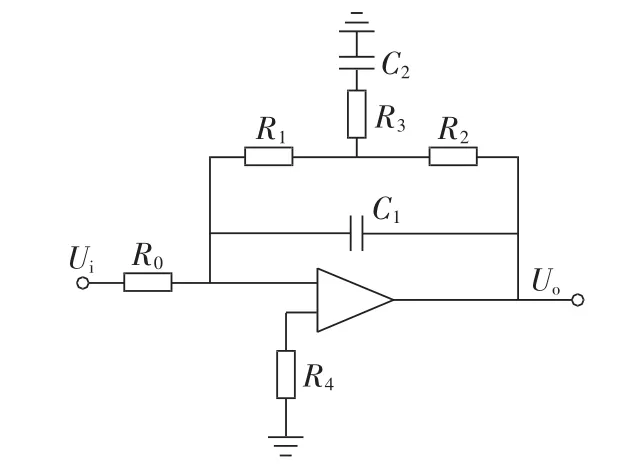
图4 低频增益平坦模拟积分器电路图Fig.4 Circuit of low-frequency gain-flattening analog integrator

该积分器的传递函数为：

其中，α1=（R1R2+R2R3+R3R1）C2；α2=R1C1+R2C1+R3C2；R=R1+R2。

通过已知的模拟滤波器设计数字滤波器，其实质就是从s平面到z平面的映射变换，通常有脉冲响应不变法和双线性不变法。但由于脉冲响应不变法本身具有频谱周期延拓的特性，会产生频谱混叠效应，所以失真较大，适用范围较小，而双线性变换法克服了这一缺陷。

双线性变换的映射关系使s平面的虚轴映射为z平面的单位圆，使模拟域-∞～∞的变化压缩为数字域频率-π～π的变化。可以令，代入式（6）中有：

由式（7）得到系统的幅频和相频特性曲线如图5所示。从幅频曲线图中可以看出，0 Hz时的幅频响应为-12 dB，即系统将直流分量衰减至原来的1/4，而将50 Hz的基波略微放大，可以有效降低直流误差的影响。但该积分器对低于20 Hz的低频干扰信号进行了幅值上的有效抑制，因此低频相移误差对测量结果影响很小，能满足电子式互感器0.2级精度的要求。

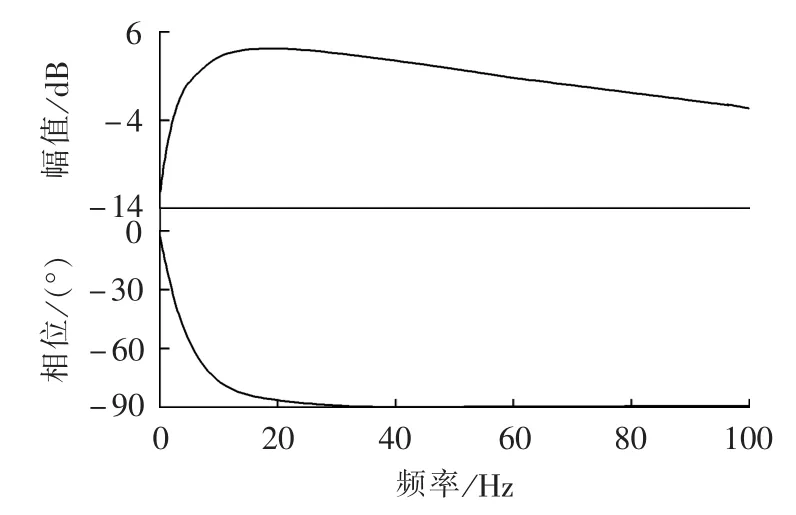
图5 低频增益平坦积分算法Bode图Fig.5 Bode diagram of low-frequency gain-flattening integrating algorithm

根据式（7）推得积分器的递推公式为：

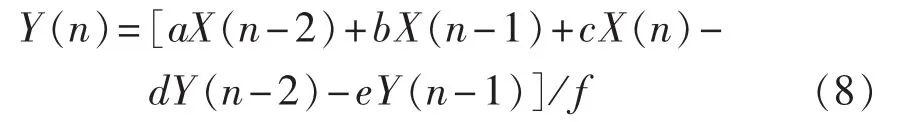
4.2 积分初值的整定

从递推公式可以看出，要通过递推求Y（n）的值，必须要获得开始递推的时刻Y（0）与Y（1）的值，而X（n）的值可以通过采集器采集获得。由于Y（n）是X（n）的积分值，因此可以根据X（n）在取极大值时Y（n）为0的特点，在 X（n）的极大值到来时进行积分。但由于X（n）在取极大值时变化较慢，因此该方法误差较大［8］。通常可以假定积分时 Y（0）与 Y（1）的初值为0，则积分后输出的Y（n）中就会叠加一个直流分量，对Y（n）进行一个周期即200点的积分得到′，取均值=′/200，再将输出的结果进行直流补偿即可。

5 电力系统暂态仿真研究

电力系统模型如图6所示，控制仿真变压器模型在0.1 s发生AB两相间50%短路故障，0.2 s消除故障，仿真总时长为0.3 s。

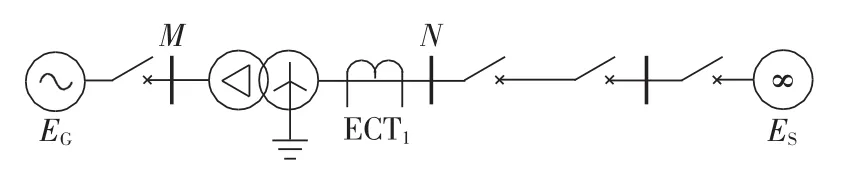
图6 电力系统仿真模型Fig.6 Simulation model of power system

互感器输出波形与原故障电流波形如图7所示。图中互感器与实际电流波形输出较吻合，正常运行情况下的误差较小；发生故障时，受故障暂态的影响，误差曲线保留了一定的暂态特性，如图8所示。

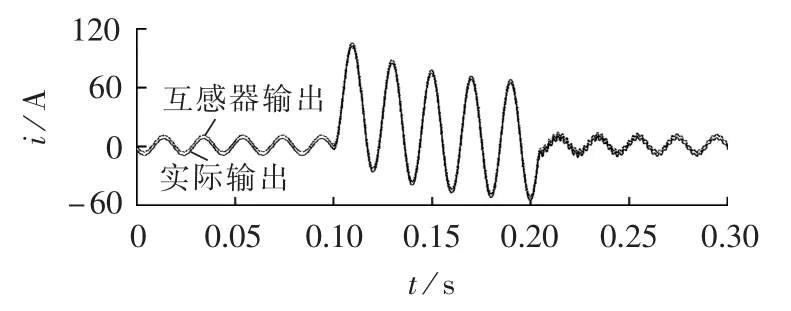
图7 互感器输出波形与原故障电流波形图Fig.7 Output current waveform of transducer and original fault current waveform

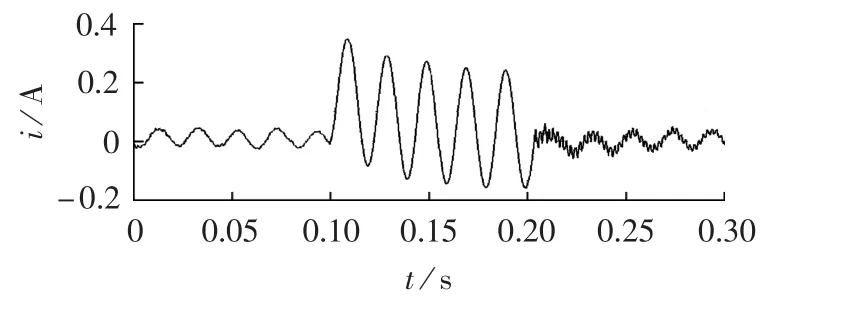
图8 误差曲线图Fig.8 Error curve

表1为数字积分的谐波相角误差与比值误差，可见采用双线性变换法得到的低频增益平坦积分算法的计算精度可以达到国家0.2级标准，额定电流下基波相角误差值小于10′，比值误差小于0.2%。

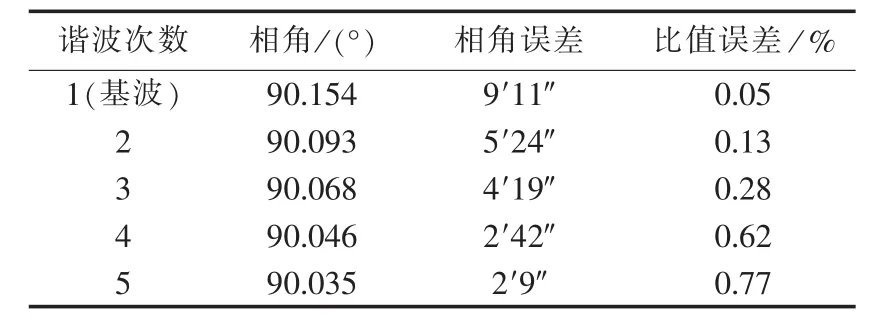
表1 数字积分的谐波相角误差与比值误差Tab.1 Phase angle error and ratio error of digital integrator for different harmonics

6 结论

本文主要研究分析了模拟积分与数字积分算法在Rogowski线圈的实际应用中的原理特性，并指出了不足之处。针对数字积分器在处理低频干扰上的不足，设计出了基于低频增益平坦模拟积分器的数字积分算法，大幅降低了低频噪声干扰，有效提高了测量精度。