一种求解最小负荷裕度的混合算法
张 峰 ,董晓明 ,梁 军 ,韩学山 ,孙 华 ,刘 宁
(1.山东大学 电气工程学院,山东 济南 250061;2.山东劳动职业技术学院 电气及自动化系,山东 济南 250022;3.山东德州供电公司,山东 德州 253008)
0 引言
连续潮流[1-14]CPF(Continuation Power Flow),从已知潮流断面出发,按照某一预先设定的模式增加发电与负荷,计算负荷所能达到的静态电压稳定极限功率(下文称为负荷裕度),能有效识别鞍节分岔点 SNB(Saddle Node Bifurcation)和极限诱导型分岔 LIB(Limit Induced Bifurcation),同时计及无功调节设备的动作,在静态电压稳定分析领域获得广泛的应用。
假设发电增长模式给定且不考虑有功限制,则负荷裕度仅与负荷增长模式有关。文献[15]则利用SNB处负荷裕度与负荷增长模式的灵敏度,修正CPF负荷增长方向,计算SNB边界的最小负荷裕度。上述方法仅针对SNB边界进行了分析,文献[16]在文献[17]的基础上进一步计及了LIB,综合计及SNB与LIB成为求取最小负荷裕度的算法要求。文献[18]从一个小节点算例中得到SNB边界非凸的结论,针对非凸问题的全局寻优能力成为评价算法优劣的另一重要因素。
考虑到CPF算法在类型的识别与计及无功设备投切等方面的优势,以及模拟退火粒子群优化[19]SAPSO(Simulated Annealing Particle Swarm Optimization)算法良好的全局寻优能力,本文在分别对CPF以及SAPSO算法进行改进的基础上,提出了一种混合算法。在CPF模型中,增加负荷增量功率因数作为负荷增长方向的约束条件;计及无功补偿设备的投切;提出一种LIB的识别算法;改进步长控制策略。在SAPSO算法中,采用变权重系数[19]与变学习因子[19]策略;提出基于功率增长方向夹角的早熟判据以及一种随机变异算法。在程序实现方面,采用多线程并行技术,充分利用计算资源提高计算速度。算例分析表明了本文研究的有效性。
1 CPF扩展潮流模型
CPF扩展潮流方程如式(1)所示:
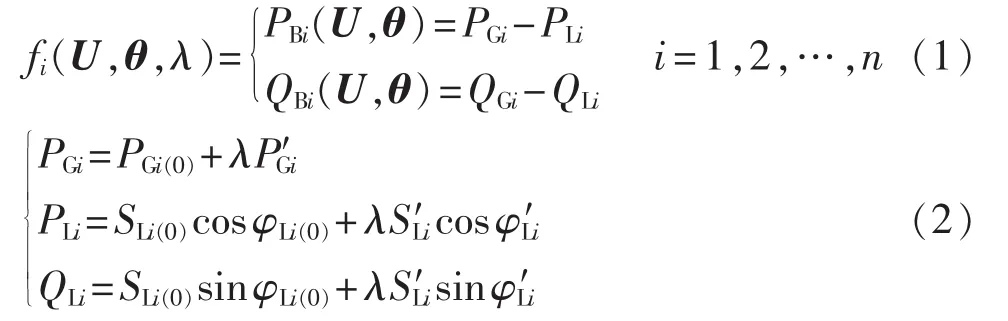
其中,λ反映功率增长水平;n为除平衡节点外的节点总数;PBi、QBi为注入节点i的有功与无功功率;PGi、QGi为注入节点i的发电机有功以及无功功率;PLi、QLi为注入节点i的负荷有功以及无功功率;U和θ分别为各节点电压幅值和相角组成的向量;P′Gi为节点 i发电机有功增长比例;S′Li与 φ′Li分别为节点 i负荷视在功率增长比例及负荷增量的功率因数角。
2 最小负荷增长模式
假设发电增长比例给定,功率增长模式仅由负荷增长比例确定,以负荷裕度最小为目标的优化模型如下所示:
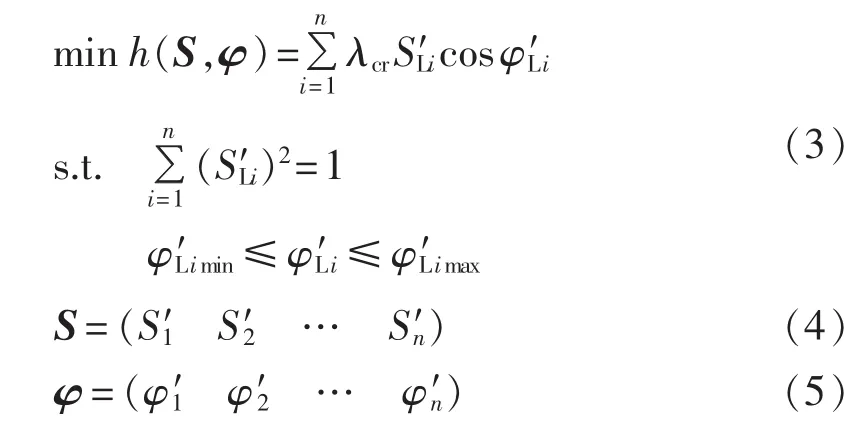
其中,λcr为分岔点对应的λ值;目标函数h(·)表示负荷裕度;φ′Limax与 φ′Limin为负荷增量的功率因数角上、下限值。
为消除等式约束,对优化模型作如下转化:
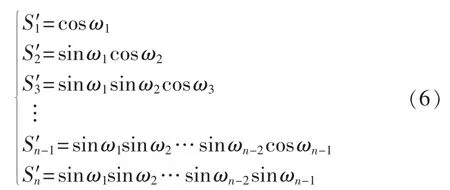
式(4)被式(7)所示决策量替代。
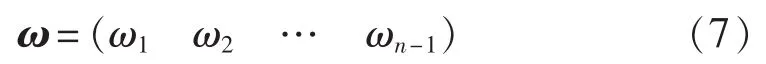
目标函数转换为:
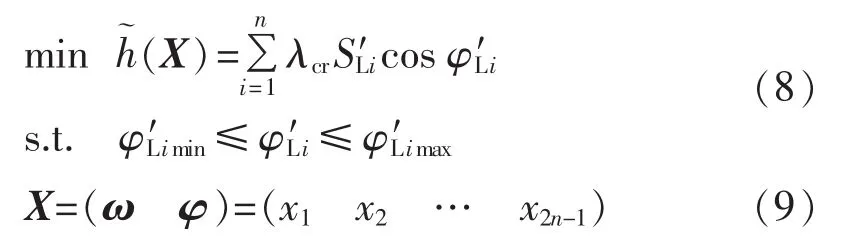
3 CPF计算过程
CPF扩展潮流方程式(1),可简写为如下形式:

3.1 步长控制策略
采用切线预测方法计算预测点:
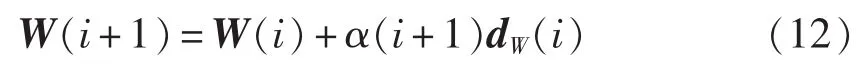
其中,W(i)为前一次校正过程收敛的潮流解;dW(i)为切线预测向量;α为步长控制因子。
本文在文献[11]的基础上,提出如下步长控制策略:
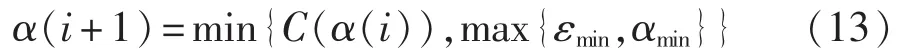
其中,C(·)表示文献[11]中的算法,αmin为 α 下限值。参数ε如式(14)所示。
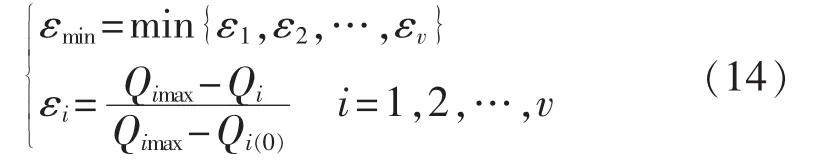
其中,v 为 PV 节点个数,Qimax、Qi、Qi(0)分别为 PV 节点i无功的上限值、当前值、初始值。
3.2 LIB的识别
式(12)中切向量的计算需要求解如下方程:
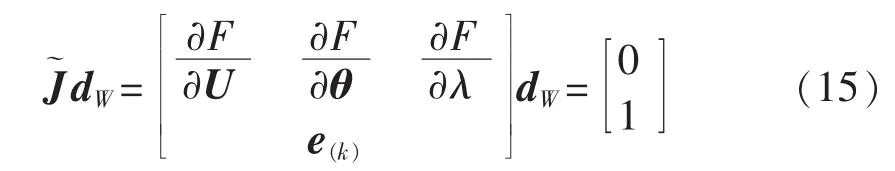
其中,e(k)是第k个分量为1、其余分量为零的向量,可根据文献[11]中的方法计算k值。常规潮流方程雅可比矩阵J为的子阵,如式(16)所示。

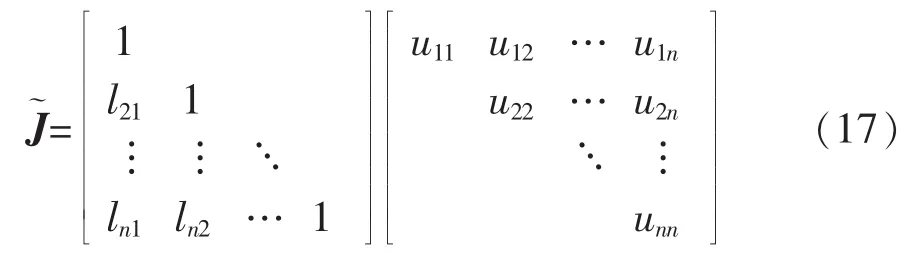
其中,lij为下三角矩阵中元素,uij为上三角矩阵中元素。
J的行列式可由下式得到:

当PV节点因无功限制转换为PQ节点后,J的维数增加,特征值数量增加。若出现正特征值,则转换前后J的行列式如式(19)所示,出现LIB。

其中,J(i-1)、J(i)分别为 PV 节点转换为 PQ 节点前、后潮流方程的雅可比矩阵。
3.3 无功补偿设备的投切
系统运行时,一般根据母线电压及功率因数是否越限调节无功补偿装置。可按如图1所示流程修正节点导纳矩阵。
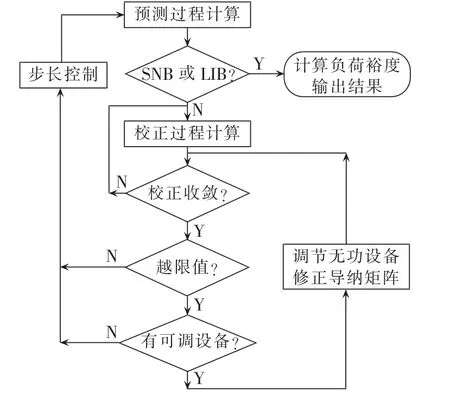
图1 CPF流程图Fig.1 Flowchart of CPF
4 SAPSO算法
对于PSO的每个粒子,被优化函数式(8)所决定的最小负荷裕度被称为粒子的适应值,如式(20)所示。
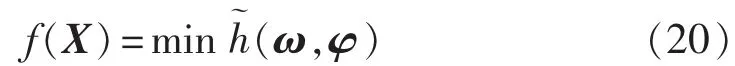
粒子l在m维空间的位置及其飞行速度可表示为式(21)与式(22)。
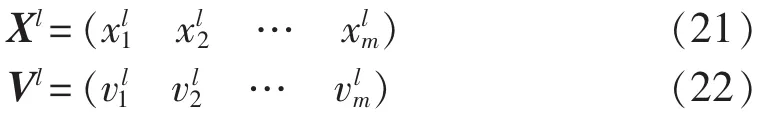
搜索过程中,粒子l所经历的最好的位置用式(23)表示。在总数为q的群体到目前为止发现的全局最优位置,用式(24)表示。

PSO算法按式(25)生成粒子d+1次迭代过程的新位置和速度。
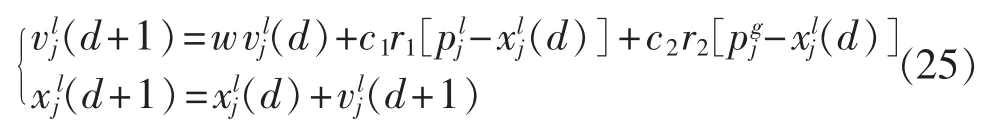

其中,w为权重系数,c1和c2为学习因子,r1和r2为服从[0,1]上均匀分布的随机数。
4.1 模拟退火操作
按式(26)定义适配值向量。
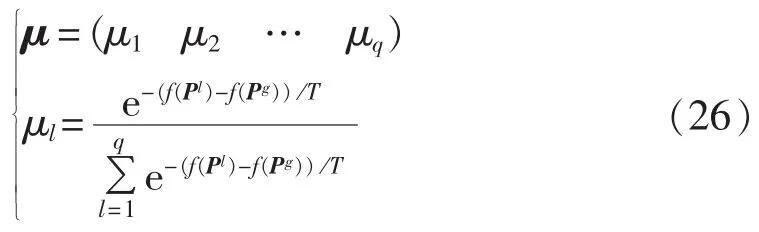
其中,T为按式(27)计算的温度系数。
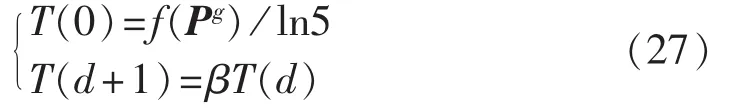
其中,β为退火常数。
根据式(28),选择粒子l的当前位置Xl替换式(25)中的Pg,计算粒子新的位置和速度,其中r是服从[0,1]上均匀分布的随机数。

在计算初始阶段,模拟退火具有概率突跳的能力,有效避免陷入局部最优;在计算后期随着温度的下降,主要围绕在全局最优粒子附近进行计算。
4.2 变权重系数与变学习因子
为提高算法的全局寻优能力,本文采用了式(29)所示的线性递减权重方法以及式(30)所示的变学习因子算法。

其中,wmax和wmin分别为权重系数的上、下限值,cmax和cmin分别为学习因子的上、下限值,dmax为粒子群最大迭代次数。
4.3 约束条件的处理
如果粒子l位置超越限值,则保留Pl,按照式(31)所示,将越限分量设为上限(或下限)值,同时将对应的粒子飞行速度分量设定为0。
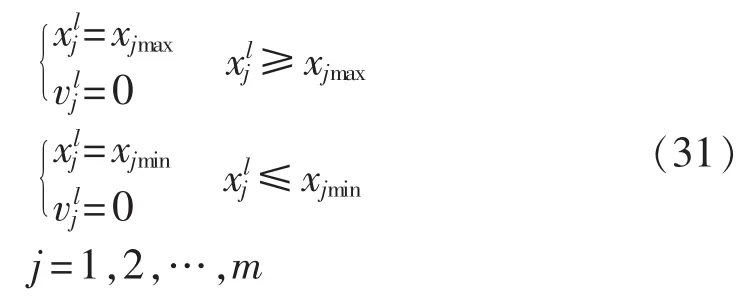
其中,xjmax和 xjmin对应式(3)中的 φ′Limax与 φ′Limin。
4.4 对于早熟的处理

通过式(32),可以计算出与向量X相对应的向量 Y,如式(33)所示:

当式(34)所示指标ρ大于限值ρmax时,则认为出现早熟。式(34)中,Yl和 Yg分别对应 Xl和 Pg。
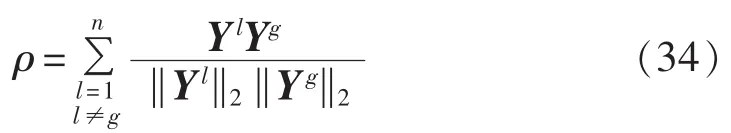
若出现早熟,则对各个粒子生成服从[0,1]均匀分布的随机数rl,若rl满足式(35)则保留该粒子的个体最优解,重新随机生成粒子l的位置和速度。

4.5 并行计算的处理
在PSO算法每次迭代过程中,都需要对各粒子进行适应值计算,如图2计算流程所示。常规方法是顺序循环执行粒子的计算任务,而本文在程序设计时利用了各粒子的计算任务相对独立的特点,为各粒子的计算分别建立线程,由操作系统选择空闲CPU并发线程计算,各线程以共享内存的形式分享粒子的个体经验和群体经验,可以有效提高计算资源的占用,节省计算时间。
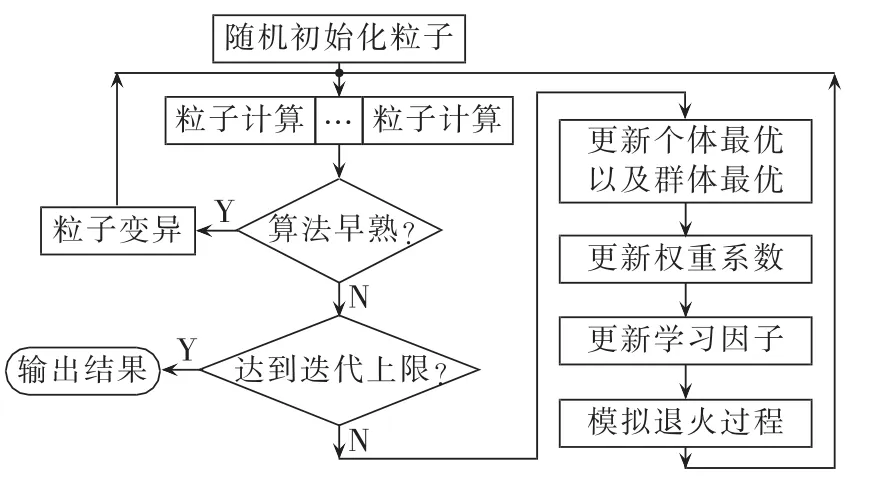
图2 SAPSO流程图Fig.2 Flowchart of SAPSO
5 算例分析
5.1 环境参数
程序的编写、调试与运行的软、硬件环境如表1所示。
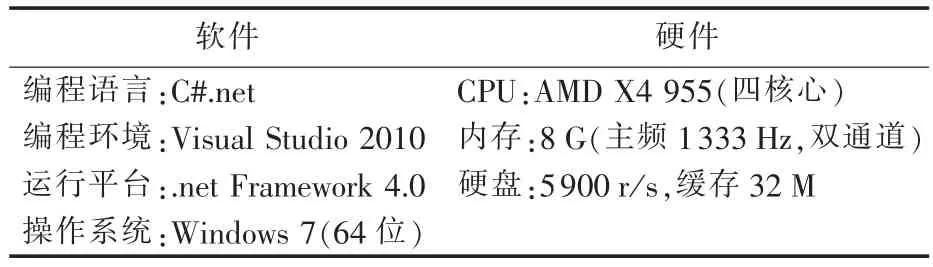
表1 算例的软、硬件环境Tab.1 Software and hardware environment of case study
5.2 算例1
图3为IEEE5节点测试系统,图中所有数据均为标幺值(系统基准功率100 MW)。
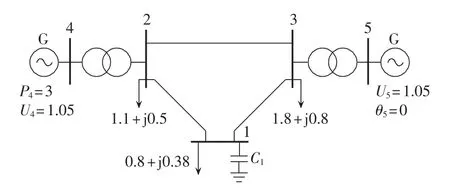
图3 IEEE 5节点测试系统接线图Fig.3 Connection diagram of IEEE 5-bus test system
节点 5是平衡节点;PV节点4的有功功率保持恒定,无功功率上限1.8 p.u.;并联电容器 C1,容抗绝对值0.018p.u.,初始状态为切除。功率因数角约束如式(36)所示,其余计算参数如表2所示。
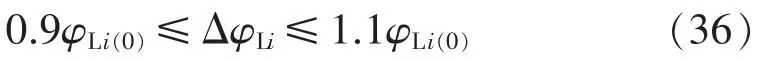

表2 计算参数Tab.2 Calculation parameters
应用本文混合算法,反复计算5次的平均耗时为4.6 s,算例表现出较好的收敛性,目标值随迭代次数的增加不断逼近最优值,如图4所示,图中最小负荷裕度为标幺值。
最小负荷裕度及其对应的负荷节点功率增量如表3所示,表中数据均为标幺值。

表3 负荷节点有功和无功增量Tab.3 Active and reactive power increments of load buses
比较并行计算方法和常规计算方法的运算速度及其对多核CPU的平均占用率,如图5所示。
由于采用并行策略,充分利用冗余的计算资源,运算速度获得了明显的提升。
5.3 算例2
图6所示系统,PV节点有功都恒等于初始值,负荷有功增量仅由平衡节点承担,利用本文方法进行最小负荷裕度分析。
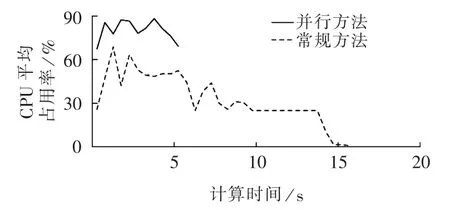
图5 CPU平均占用率Fig.5 Average rate of CPU occupancy

图6 IEEE 30节点测试系统接线图Fig.6 Connection diagram of IEEE 30-bus test system
计算时间 8分 17秒,PV 节点 2、5、8、11和 13由PV节点转换为PQ节点,采用本文方法对其进行识别,均未见LIB。最终计算得到最小负荷裕度为0.5932 p.u.(临界点类型为 SNB)。
由于篇幅限制,表4中仅列出负荷变化较多的部分节点的计算结果,表中数据均为标幺值。可见,以节点29与节点30为首的负荷增长模式,是计及静态电压稳定的最“危险”增长模式。
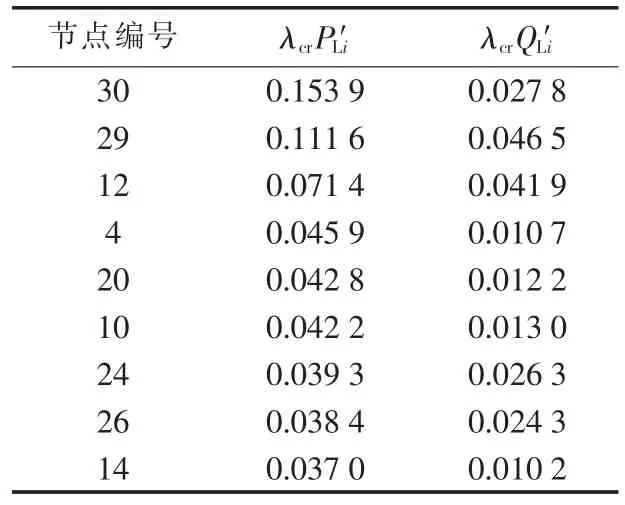
表4 最小负荷裕度对应的负荷变化Tab.4 Load variation along with minimum load margin
6 结论
SAPSO算法是一种实用性较强的随机搜索进化算法,能有效地避免搜索过程陷入局部极值,具有较好的全局寻优能力;CPF算法模拟电力系统负荷增长的过程,可以有效识别各种分岔类型以及计及无功设备的动作。本文有机结合2种算法的优势,混合算法表现出良好的收敛性,并行计算充分利用计算资源,最大限度提升算法的应用性能,算例验证了本文算法的有效性。

