基于量子免疫克隆算法的多目标无功优化

罗 毅，多靖赟

（华北电力大学 控制与计算机工程学院，北京 102206）

0 引言

电力系统无功优化是指从优化运行的角度调整系统中各种无功控制设备的参数，在满足节点正常功率平衡及各种安全指标的约束下，实现目标函数最小化的过程［1］。它既是保证电力系统安全、经济运行的有效手段之一，又是降低网络损耗、提高电压质量的重要措施［2］。

无功优化是一个多目标、多约束、变量类型混合的非线性规划问题。关于无功优化的求解方法可分为传统数学算法和现代启发式算法。传统数学方法有非线性规划法［3］、简化梯度法［4］、内点法［5］等，这类方法有一定的优越性，但计算较为复杂，易陷入局部最优解，且不便于处理离散变量。随着人工智能的发展和计算机运行速度的提高，越来越多的现代启发式算法应用于无功优化中，如遗传算法［6］、蚁群算法［7］、免疫算法［8］、粒子群算法［9-10］、搜索禁忌算法［11］、模拟退火算法［12］等，且都取得了一定的研究成果。量子计算因其强大的运算能力，已经成为世界各国紧密跟踪的前沿研究领域之一。借鉴生物免疫系统原理而发展起来的免疫算法也已成为现代启发式算法的一个研究热点。结合量子计算机理和免疫克隆算子，本文提出了一种解决多目标无功优化问题的量子免疫克隆算法 QICA（Quantum Immune Colonial Algorithm）。该算法具有良好的并行性，搜索速度快，寻优能力强，将全局搜索和局部寻优有机结合，确保所得解集快速有效地从不可行域边缘和可行域内部向最优Pareto前端逼近，而且可以有效防止退化现象的产生，是求解多目标无功优化问题的有效方法。

1 多目标无功优化数学模型

1.1 目标函数

本文选取有功网损PL最小、静态电压稳定裕度VSM（Voltage Stability Margin）USM最大以及节点电压平均偏移量ΔU最小作为目标函数。

a.有功网损。

其中，NL为系统支路总数；δi、δj、Ui、Uj分别为节点 i、j电压的相角和幅值；Gk（i，j）为支路 k 的电导。

b.静态电压稳定裕度。

选用收敛潮流雅可比矩阵的最小奇异值作为度量系统静态电压稳定裕度的指标［13］，即：

其中，JJacobi为收敛潮流雅可比矩阵，eig（JJacobi）为雅可比矩阵的特征值，为该矩阵最小特征值的模。

c.电压平均偏移量。

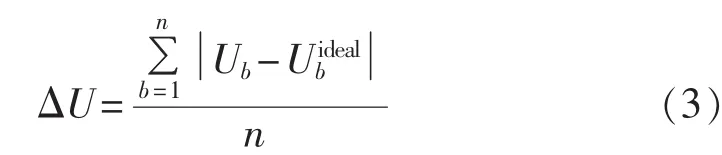
1.2 约束条件

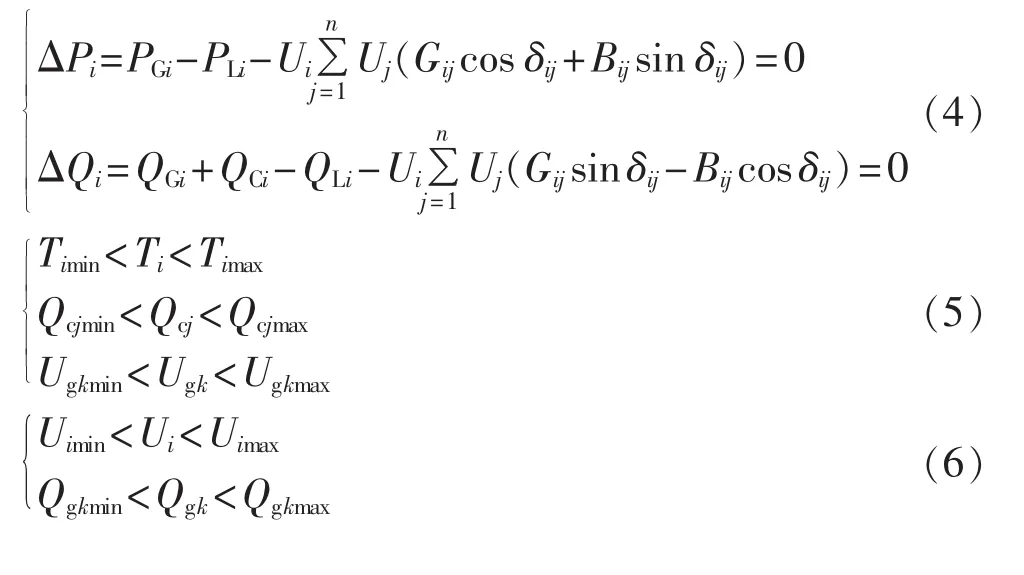
其中，T为可调变压器的变比；Qc为无功补偿电容器容量；Ug为发电机端电压；U为各节点的运行电压；Qg为发电机注入无功；Timin（Timax）、Qcjmin（Qcjmax）、Ugkmin（Ugkmax）、Uimin（Uimax）、Qgkmin（Qgkmax）分别为以上变量所对应的最小（最大）值。式（4）—（6）分别为系统潮流约束、控制变量约束、状态变量约束。

1.3 多目标函数解评价

多目标函数之间存在相互矛盾性，所以很难找到一个解，同时使各目标函数达到最优。传统加权叠加比较的评价方法，对权重选取的依赖性很大，而且不能很好地反映各目标函数的优劣性，本文采用目标函数值与理想化目标的接近程度来评价解的优劣性，其操作如下。

若多目标函数 min（F）=min（f1，f2，f3，…，fc）存在一组可行解 x1、x2、…、xl。

a.构建目标函数矩阵。

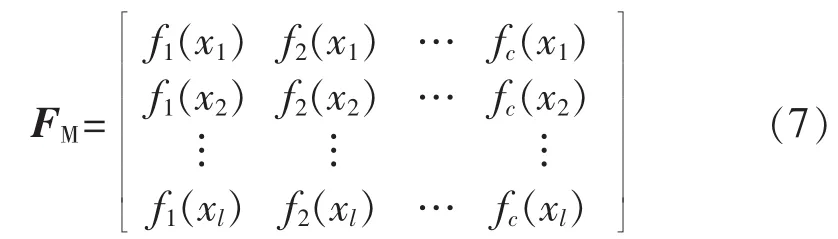
b.目标函数矩阵归一化处理。

c.求取理想化目标。所谓理想化目标即归一化矩阵中各函数对应的最小值。

d.评价各解的优劣性。本文采用各目标函数值与理想化目标欧氏距离的大小来评价解的优劣性，该距离越接近表明解越优。

2 量子免疫克隆算法

2.1 克隆算子

在多目标优化问题中，Pareto前端上的所有点是同等优秀的，为了保证在种群扩张时，所得解在Pareto前端均匀分布，本文采用了自适应克隆操作。抗体的克隆规模依据拥挤距离［14］来自适应地调整，即拥挤距离越大者，克隆规模就越大，被搜索的机会越多，其具体操作如下。

将抗体群 A（it）=｛W1，W2，W3，…，Wk｝中抗体 Wi以比例qi进行克隆，其中qi为：

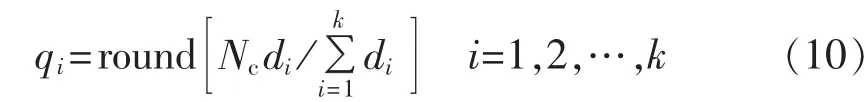
其中，it为当前的进化代数；round［·］表示取整为最近的整数；Nc为与克隆规模有关的设定值，本文取Nc=200；di为拥挤距离（具体形式参见文献［14］）。

则克隆后的抗体群为：

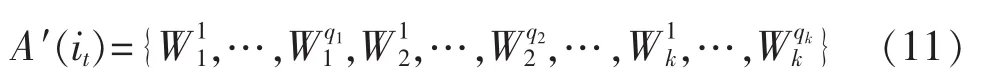
2.2 量子重组算子

混沌变量在寻优过程中具有随机性、遍历性以及规律性等特点。本文通过量子重组算子将Logistic映射［15］下的混沌序列用于量子抗体的寻优过程中，使量子位在演化过程中呈现出混沌现象，进而极大增加了算法的搜索能力，其操作如下：

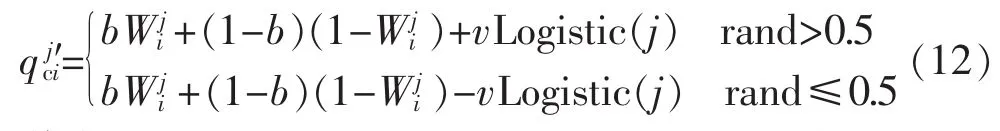
其中，i=1，2，…，k；j=1，2，…，qi；Logistic（j）为 Logistic映射的第 j个序列值（具体形式参见文献［15］）；b为抗体影响因子，取值范围为［0.1，0.4］；v为混沌收缩因子，取值范围为［0.1，0.3］；rand 表示生成 0～1之间的随机数。

2.3 量子非门算子

为进一步增进种群的多样性，抗体经上述量子重组操作后，以变异概率pm随机选择一位或若干位进行量子非门操作，本文取pm=0.5。该操作实现了对量子位概率幅的互换，使得原来取状态0的概率变为取状态1的概率，或者相反。其具体操作如下：

其中，Q为量子位概率幅。

2.4 选择更新算子

传统免疫算法绝大多数依据亲和度函数作为选择方式，抗体亲和度越大，越容易被选择保留。在本算法中，一个抗体能否通过选择进入下一代，取决于该抗体是否为当前代中的非支配抗体。当进化到达一定代数时，非支配抗体数目可能会有很多，而依据本算法的选择策略，它们都将被选入下一代，这样会导致运算速度变慢。为了避免该情况发生，本算法采用了抗体群更新操作。如果非支配抗体超过一定数目Nn，则可依据拥挤距离将Pareto前端上分布较为密集抗体删除，既保证了运算速度，也保证了所得解分布的均匀性［16］。

2.5 免疫疫苗

传统免疫算法由于缺乏适当措施，在寻优过程中会出现大量劣解、甚至非可行解。为了有效地克服此类退化现象，本文引入了疫苗［17］的概念。选择当前代精英个体作为免疫疫苗保留，并于下一代量子非门操作完成后植入种群，从而在寻优的过程中有效地克服了退化现象，保证种群向优良模式进化。

3 基于量子免疫克隆算法的无功优化

3.1 抗体的编码

本算法中的抗体采用量子位表示，一个量子位不仅可表示0、1这2个状态，而且可以表示在0、1这 2个状态间的任意状态。若用n个量子位表示可调变压器的变比T、m个量子位表示发电机端电压Ug、l个量子位表示无功补偿电容器容量Qc，则编码后的每一个抗体可以描述为：

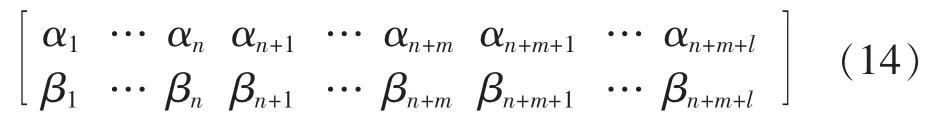
其中，αi、 βi（i=1，2，…，n+m+l）为复常数，表示第i个基因位取值0的概率，表示第i个基因位取值1的概率。

3.2 不等式约束处理

不等式约束将搜索空间划分为可行域和不可行域2个部分，因此如何有效地利用不可行解显得非常重要。传统免疫算法未考虑到不可行解集，仅对可行解集进行相应的进化计算。本算法有效利用部分接近可行域边缘的不可行解，使寻优过程分别从不可行域边缘和可行域内部向约束最优Pareto前端逼近，从而保证了所得约束最优解的较高质量。

不等式约束 g（x）=（g1（x），g2（x），…，gh（x））≤0可转化为一个目标函数，令：

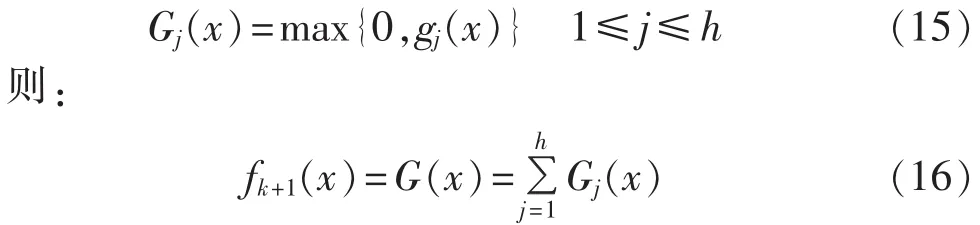
对任意一个变量 x，若 fk+1（x）=0，则 x 满足约束条件，为可行解；若 fk+1（x）＞0，则 x不满足约束条件，为不可行解，并且fk+1（x）的数值越大，则x违反约束的程度越严重。因此，可采用如下处理方法：

b.以Pareto占优的概念为依据，将可行解集Xf划分为非Pareto占优集和Pareto占优集Ps；

d.分别对有益解集Qb和可行解集Xf进行相应的免疫克隆选择操作，求得高质量的Pareto最优解。

3.3 算法流程

量子免疫克隆算法应用于多目标无功优化的流程如图1所示。

4 算例分析

为验证本算法的可行性，本文对IEEE 14节点测试系统进行多目标无功优化计算。用MATLAB语言编制了系统潮流计算程序和量子免疫克隆算法。算法中相关参数的设置如下：抗体群规模为100，有益解集规模为30，最大迭代次数为50。算例中数据均为标幺值。

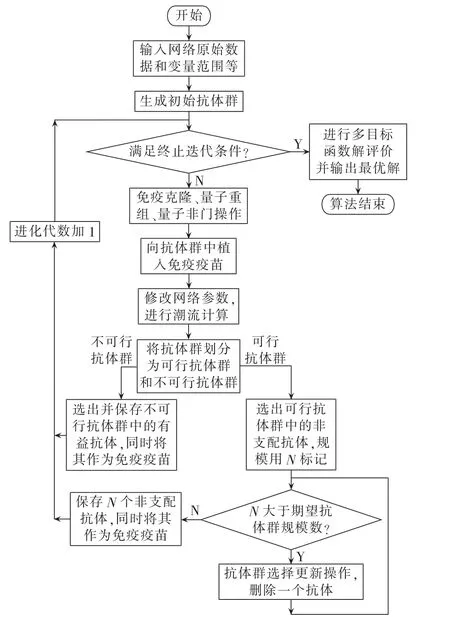
图1 基于量子免疫克隆算法的多目标无功优化流程Fig.1 Flowchart of multi-objective reactive power optimization based on quantum immune colonial algorithm

4.1 IEEE 14节点系统算例

该系统包含3台可调变压器、5台发电机（其中1号发电机为平衡节点）、1个无功补偿点。各可调变压器上下档位数为±16，步进量为0.625%，其变比范围为0.9～1.1；各发电机端调压范围为0.95～1.05；无功补偿点（节点9）的无功补偿上限为0.5，分段步长为0.1。

4.2 分析与比较

运用本文算法对该系统进行优化评价，将该算法独立运行50次后选出有代表性的一组计算结果如表1所示。

图2显示了该次计算最终求得Pareto解的分布，其中方块符表示决策最优解。

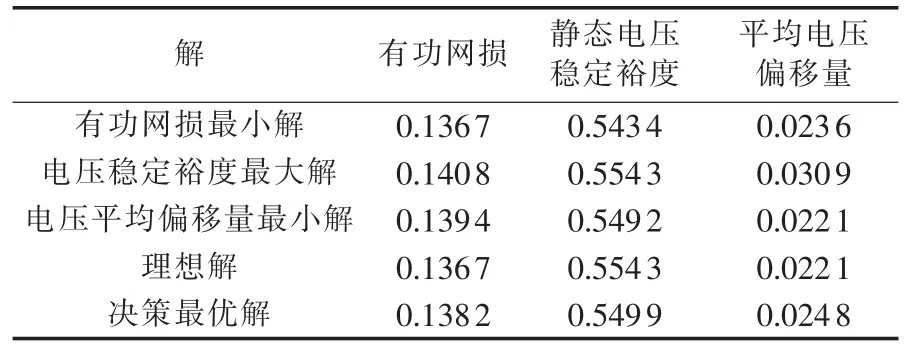
表1 IEEE 14节点测试系统多目标无功优化结果Tab.1 Results of multi-objective reactive power optimization for IEEE 14-bus test system

由表1和图2可见，最优解所对应的点坐标与理想化目标所对应的点坐标之间存在一定距离，这说明了多目标无功优化中各个目标函数同时达到最优化的可能性很小，也验证了求解相互矛盾的多目标函数只能根据实际情况从一个整体最优化的角度求出可行解，而应用本文所提出的欧氏距离来评价可行解的优劣则可以较好地履行这一职责。

将本文算法独立运行50次后，求出所得最优解的平均值，同时将该值与其他算法应用于IEEE 14节点系统的结果进行了比较，如表2所示。

图2 算法Pareto解的分布Fig.2 Distribution of Pareto solutions

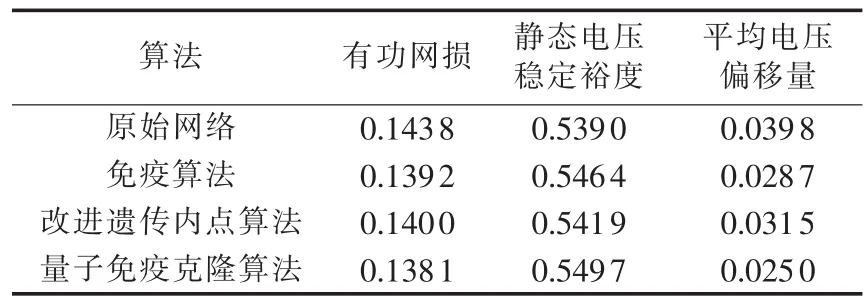
表2 算法优化运行结果比较Tab.2 Comparison of optimization results among algorithms

可见，本文提出的算法在多目标无功优化问题中应用效果明显，较免疫算法和改进遗传内点算法［1］可更好地找出全局最优解，进而有效降低了网络损耗，提高了电压质量。

5 结论

本文提出了一种量子免疫克隆算法，并将其应用于求解电力系统无功优化问题。该算法搜索速度快，寻优能力强，并将全局搜索和局部寻优有机结合，确保所得解集快速有效地从不可行域边缘和可行域内部向最优Pareto前端逼近，而且可以有效防止退化现象的产生；以提高系统经济性和安全性为前提，选用系统有功网损、节点电压平均偏移量以及静态电压稳定裕度3个指标作为系统无功优化的目标函数，通过对IEEE 14节点系统进行测试计算，验证了该方法的可行性与有效性。