高中代数思想在“密钥共享”中的应用

◆赵世棋 林昌露

(福建南安市柳城中学;福建师范大学数学与计算机科学学院)

华罗庚先生说过:“数缺形时少直观，形少数时难入微;数形结合百般好，隔裂分家万事休。”数和形是数学学习和研究的两个重要内容。在高中数学学习中，“数形结合”不仅是一个重要的代数数学思想，又是一种常用的数学解题方法。“信息安全与密码”是《普通高中数学课程标准(实验)》中选修系列3的六个专题之一。在当今信息化的社会当中，人们每天在互联网和物联网上传输、获取、交换海量的信息，这也带来更多的信息安全问题。在高中阶段对信息安全与密码知识的学习，不仅有助于培养和增强学生的信息安全意识，而且有助于培养学生应用数学的能力和学习数学的兴趣。本文将从密码学中的“密钥共享”与高中数学中的“数形结合”的代数思想入手，分析数学在信息安全与密码中的重要作用。

一、问题的提出

密钥共享的基本思想，可以通过如下例子来表述:某个银行的保险库，每天至少需要用密码(即密钥)打开一次;银行雇佣四位出纳，但是银行为提高保险库的安全性并不想将密钥委托给单个出纳。这时，银行可以利用密钥共享的方法来设计一个安全的系统保护这个密钥。在该系统中，银行把密钥分成四部分并独立分发给四位出纳;该系统保证任意三位或四位出纳同时在场才可用密钥打开保险库，而任意单独或两位的出纳不能打开保险库。此外，即使有一位出纳的那份密钥意外地丢失，其他三位出纳仍然可正常恢复整个密钥。对于上述的问题和要求，如何用一个数学的方法来有效地解决呢?

二、问题的求解

解法一:解方程组方法

1979年，著名密码学家阿迪·沙米尔利用解方程组的方法给出了一个简单且有效的方法。我们用一个简单的例子展示该方法:在数字化世界中，可假设密钥是一个数字，这是发挥数学作用的第一步。具体地，设密钥为2，四位出纳分别用1、2、3和4表示，选取一个二次多项式f(x)=2+3x+x2，它满足f(0)=2，即当x取零时，由这个多项式计算的结果恰好是密钥值2;计算f(1)=6，f(2)=12，f(3)=20和f(4)=30，并把这四个值分别秘密地分发给四位出纳。这样，我们已经完成这个保护系统的设置，该密钥的部分密钥分别由四位出纳安全地保管。假设前三位出纳同时在场，此时只需把由他们保管的秘密值6、12、20拿出来，大家就可以用解方程组的方法简单地恢复得到密钥值，计算过程如下:假设该二次方程是f(x)=a+bx+cx2，则可得到如下方程组:通过求解该方程组，可得a=2，即f(0)=a=2为密钥值。若只有一位或两位出纳同时在场，由解方程组的方法可知，则他们只能得到有一个方程或两个方程的方程组，但有三个未知数，故该秘密值无法正确地被恢复。

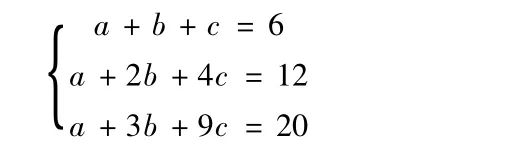
解法二:几何方法

现在，从几何角度来更直观地分析一下上述方法。我们先把出纳的代表值和各自的部分秘密值分别看成直角坐标系中的坐标点，即(1，6)、(2，12)、(3，20)和(4，30)，且把密钥也看一个坐标点(0，2)。可把二次多项式看成一条二次曲线，密钥值是该曲线与纵轴的交点，每位出纳的部分秘密值均是曲线上某个点的纵坐标值(见图1)。由二次曲线的性质可知，若已知曲线上的三个坐标点，可容易在直角坐标系上画出完整的曲线，即可以获得与纵轴的交点值;若仅知道曲线上一个或两个坐标点(如A和B，见图2)，那么该曲线与纵轴的交点可能有无数个(如:C1，C2，…，Cn)，即无法确定该密钥值。

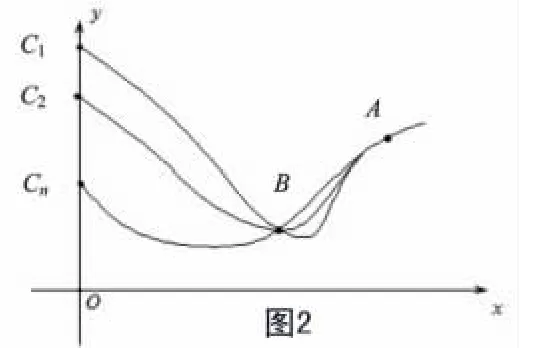
综上所述，我们分别从代数的观点和几何的观点，分析了密钥共享的基本思想，充分展现了高中代数学习中“数形结合”的思想方法。从这两个角度看问题，不仅可以让学生直观体验到数形结合的思想方法，提高学生对数学的鉴赏力和学习数学的兴趣，而且可以帮助学生对密钥共享方法的理解，提高他们对“信息安全和密码”学习的兴趣，有利于学生进一步发展，对实现“信息安全与密码”模块教学也起到探索的作用。

［1］袁智强.《信息安全与密码》教学构思及评价设想.数学通讯，2005，(11):9-10.

［2］刘木兰，张志芳.密钥共享体制和安全多方计算.北京:电子工业出版社，2008.