基于概率洪泛算法的异构无线自组网研究

刘 颖

（中国石油大学胜利学院 信息与计算科学系，山东 东营257000）

自组网又称Ad hoc网，由一组配备无线收发器的节点组成，节点可以通过无线信道互相通信。在整个自组网中，不存在固定的基础设施，节点通过分散的、自组织的方式独立于其他节点，并以任意方式保持节点间的相互联系。每个节点充当路由器将网络中的数据包转发到目的地。在典型的自组网中网络架构是均匀的，即网络中的所有节点具有相同的广播覆盖范围和平等的地位，称为同构体系结构。在网络模型中各节点通信范围互不相同的结构被称为异构体系结构。在同构自组网中平均路径长度较大、聚类系数较低，导致网络中大量的跳跃计数、端到端的较长延迟和大量的电力消耗等问题。针对这些问题，笔者设计基于异构网络体系结构的概率洪泛算法。该算法不仅能用于独立的信息传播技术，也可作为辅助工具用于其他路由算法，来进行路由发现和路由维护，利用该算法可以大大地减少信道争用和冲突。由于在该算法中网络中所有节点之间传输概率并不是均匀分配的，所以将其称为不均匀概率洪泛算法。将这种不均匀概率洪泛算法应用于异构网络，会使网络性能得到较大的提高。

1 异构网络的架构

在自组网中存在很多重要性能指标，如覆盖范围、连通性、移动性等，平均路径长度和聚类系数是其中两个非常重要的特征度量。

平均路径长度是网络中所有节点对之间的平均最短距离。在自组网络中，平均路径长度L为所有节点间最短路径长度的算术平均值，即

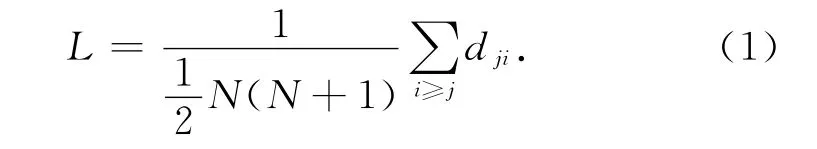
式中，dji为节点i和节点j之间的最短路径；N为网络中节点的数量。

平均路径长度L描述了网络规模，是网络中任意两点间最短路径长度的平均值。平均路径长度越短，端到端流量包的传输延迟和代价也就越小，它是衡量网络转发能力的重要参数。

聚类系数描述了网络节点的聚类效果。一个节点i的聚类系数，被定义为节点i的所有邻界边数除以它们之间可能存在的最大边缘数，即：

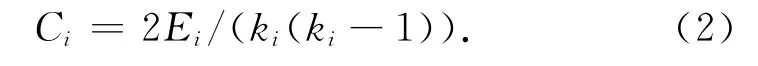
式中，Ei为节点i与相邻节点间存在的边缘的数量；ki为相邻节点数。

整个网络的聚类系数定义为平均值Ci，是节点中两个任意临界节点仍互为邻居的平均概率，应满足基本条件0≤C≤1。一个完整的随机图，如E-R图［1］的聚类系数C＝O（N-1），但在实际网络中聚类系数的值会更大。

通常在一个典型的自组网络中每个节点都配备有一对收发器，其发射功率和通信范围相同，这种同构网络架构可以被建模为随机几何图［2］。在该模式中，只要节点间的距离小于通信覆盖范围就可以互相沟通，这取决于收发器的发射功率。

在异构模式中，随机挑选一些节点，为其配备其他节点两倍通信距离远的发射器。为区别于普通节点，这些节点被称为特殊节点。为了检测特殊节点的设置对网络性能的影响，将其中一小部分节点作为特殊节点进行仿真试验。

仿真设置：将400个节点布置于平面上，以形成阵列的20行和20列中的数组。每个普通节点的通信范围要保证它最多有4个邻接节点。一个特殊节点的通信范围被设定为一个普通节点的两倍，因此，每个特殊节点将有8个邻接节点。在开始时，没有设置特殊的节点，此时形成的是一个同构网络（图1（a）），将特殊节点逐个添加（图1（b）），直到所有节点成为特殊节点（图1（c））。当所有的节点都成为特殊节点时，此时的网络再次变成了同构网络。

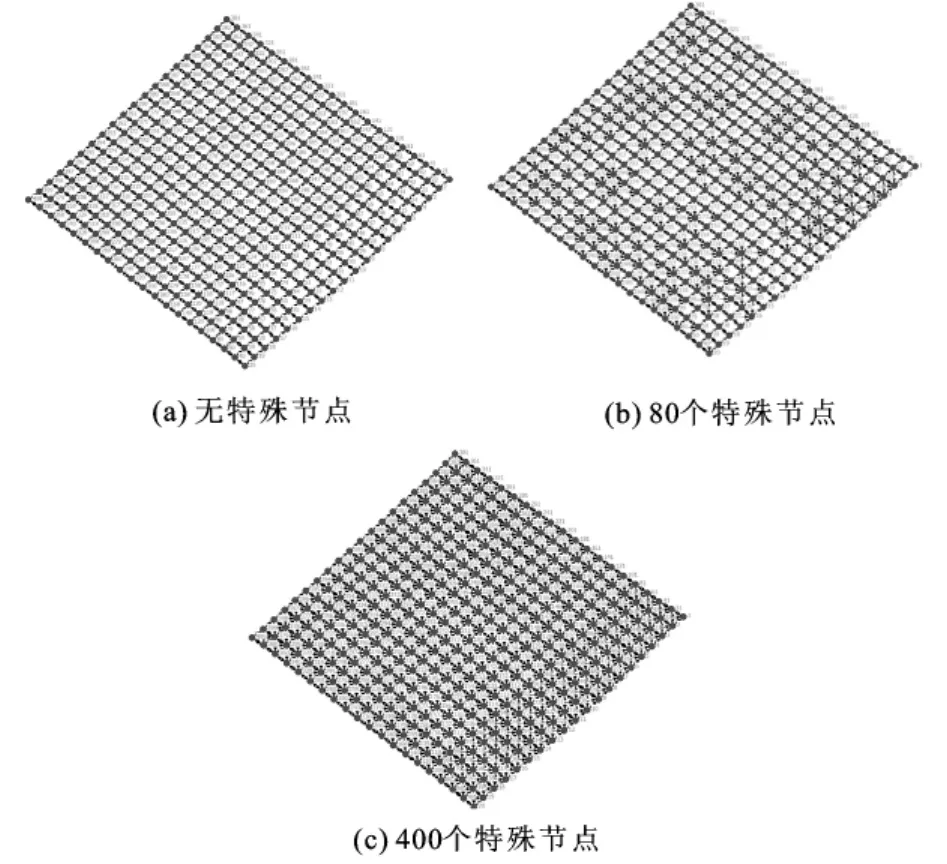
图1 仿真节点的设置

平均路径长度和聚类系数随特殊节点数量的变化见图2和图3。在网络中特殊节点从0增加到80的过程中，统计的数据显示平均路径长度和聚类系数发生了明显的改善。而从特殊节点80个开始，进一步增加特殊节点也不再带来进一步的改善。借助物理术语，这种现象称为相变［3］。相变现象表明，只有在网络中将特殊节点设定在总节点20%（80个）的范围内，才能够起到减少平均路径长度和增加聚类系数的效果。该试验的过程是实现在网格网络上，在随机网络拓扑结构模型中可得到相同的结论。

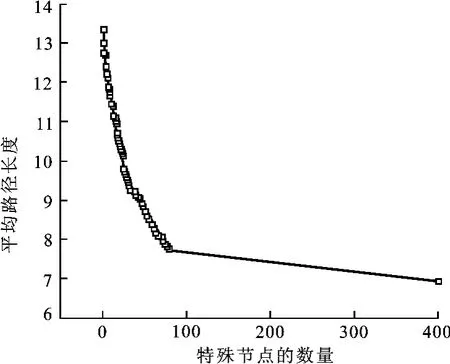
图2 异构网络模型的平均路径长度

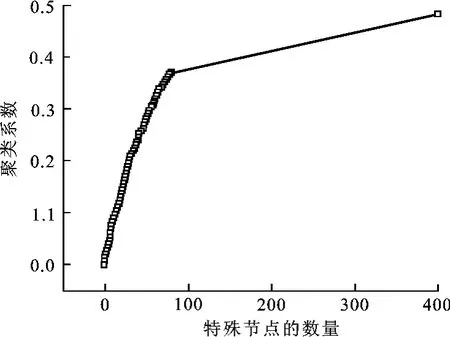
图3 异构网络模型的聚类系数

2 不均匀概率洪泛算法

概率洪泛算法由约阿夫萨森［4］最早提出，被证明是存在于自组网络中的一种有效的信息传播技术。传统的洪泛算法要求移动广播消息要尽可能快地到达目的地，但这种方式将会产生大量数据包的碰撞。在传统洪泛方法中将节点接收到广播消息的概率值设置为1，而在概率洪泛算法策略中节点接收到广播消息的概率为0＜P＜1。根据渗流理论，当P增加时，数据包传送率将经历一个从0到1的突然过渡。这就是说，会存在一个临界值Pc，当洪泛概率超过该值时，传播的速度将不会再有明显提高。

接下来将针对异构网络模型设计一个新的概率洪泛算法。在异构模型中，为每个节点配置一个发射器和两个接收器。有两个传输的频带可覆盖整个网络，为特殊节点配置一种发射器，针对其他普通节点配置一种发射器。所有节点都可以接收和处理两个频带的信号。将特殊节点的发射机的功率设置为普通节点通信距离的2倍，同时赋予给特殊节点比普通节点大的传输概率，因此这种算法被称为不均匀概率洪泛算法。为将一般的概率洪泛算法的性能与不均匀概率洪泛算法进行比较，在进行仿真的试验过程中，利用OPNET软件来模拟网络仿真环境。

首先，进行架构在同构网络基础上的普通概率洪泛算法仿真试验，在平面尺寸为2 000m×2 000 m的范围上随机设置400个节点，将节点的通信半径设定为200m。区域中心（1 000，1 000）附近的一个节点被选定为广播源点而其他节点作为目的地。在仿真试验中，传输概率从0到1逐渐增加，对目标数据进行收集。对节点收到的数据包的数量和跳数进行统计，用以测试网络的覆盖区域和平均路径长度。

其次，进行架构在异构网络基础上的不均匀概率洪泛算法的仿真设置，在本次仿真试验中，共设置了80个特殊节点，占总结点数的20%。将特殊节点的通信范围设定为300m，而将普通节点的通信范围设置为150m，仿真试验结果见图4和图5。

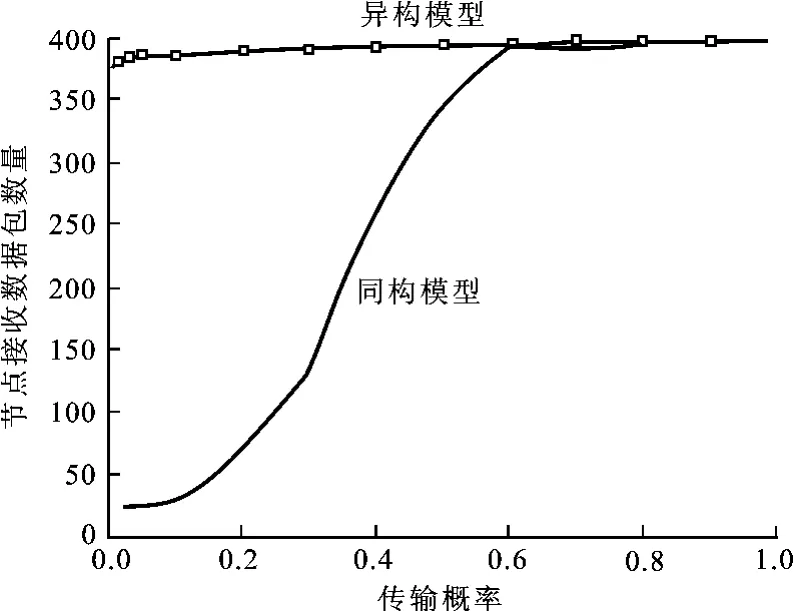
图4 数据包投递率的比较

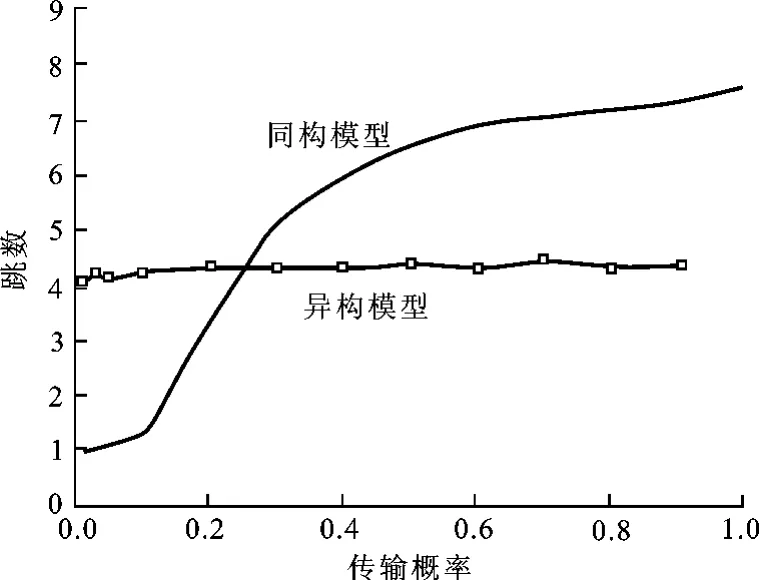
图5 跳数的比较

对试验结果进行分析。首先，在不均匀概率洪泛算法与异构网络模型相结合的仿真试验中，用0.2的传输概率获得了90%的网络广播覆盖，但架构在同构网络基础上的普通概率洪泛算法仿真试验则需要超过0.6的传输概率才能实现同样范围的广播覆盖。其次，前一种模型中的跳数要远远小于后者，这就意味着短的传输延迟。最后，在异构模型中，320个普通节点其通信半径是150m，80个特殊节点的通信半径为300m。而同构模型中的所有节点都是200m的通信距离。通过无线传输计算公式可以得出，在自由空间损耗前者比后者约小13.75%。

试验表明，将不均匀概率洪泛算法与异构网络模型相结合，其性能要优于架构在同构网络基础上的普通概率洪泛算法。

3 结束语

基于概率洪泛算法的异构网络模型的明显优点主要体现在平均路径长度和聚类系数这两项主要指标上，另外在成本比较上其耗电量只有传统网络的20%，能减少广播碰撞，实现短的传输延迟，并减少功率消耗。这种新算法的实现简单，易于实现低成本的控制，同时应该指出的是，由于特殊节点的存在，需为特殊节点配备专用发射功率的收发器。

［1］BOLLOBAS B.Random graphs［M］.Cambridge：Cambridge U-niversity Press，2001：143-147.

［2］PENROSE M.Random geometric graphs［M］.Oxford：Oxford University Press，2003：22-45.

［3］KRISHNAMACHARI B，WICKER S B ，BEJAR R.Phase transition phenomena in wireless Ad hoc networks［J］.Global Telecommunications Conference，2001（5）：2921-2925.

［4］SASSON Y，CAVIN D，SCHIPER A.Probabilistic broadcast for flooding in wireless mobile Ad hoc networks［J］.2003IEEE Wireless Communications and Networking Conference Record（Cat No 03TH8659），2003（2）：1124-1130.