基于空间矢量控制的零磁通短路电流限制器的研究
许素芳 ,岳长城
(胜利石油管理局 电力管理总公司,山东 东营257000)
随着电力系统规模的不断扩大、分布式电源的增加,输电线路的电流水平不断提高,短路电流水平也大大增加。当出现短路故障时,对断路器开断容量的要求增大,同时对输电线路以及电力系统一次二次设备也会产生很大影响。为了保护电力系统设备,减小断路器开断容量,需要将短路电流水平控制在一定的范围内。短路电流限制器(fault current limiter—FCL)是现代电力系统中的重要装置。笔者拟在零磁通短路电流限制器的基础上对基于空间矢量控制方法的零磁通短路电流限制器进行研究。
1 零磁通短路电流限制器基本原理
1.1 工作原理
基于零磁通的短路电流限制器的工作原理[1]是将变压器的一次侧串联接入系统之中。变压器的T型等效模型如图1所示。
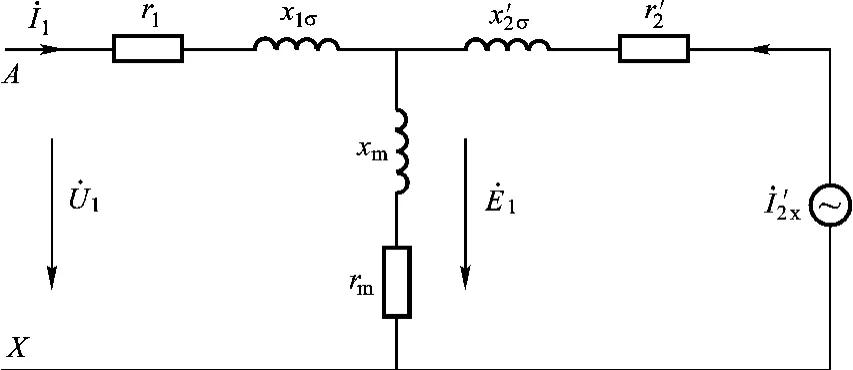
图1 变压器的T型等效电路
当系统正常工作时,在变压器的二次侧注入与一次电流反向的二次电流,那么这个二次电流产生的磁场将与一次电流产生的磁场相抵消,如果满足F=ω1˙I1+ω2˙I2x的条件[1](F为铁心中合 成 磁 动势),那么磁通补偿为0,接入系统中的变压器阻抗仅仅为变压器一次侧阻抗。变压器的等效模型如图2所示。

图2 进行磁通补偿时变压器等效电路
此时串接进入系统中的变压器一次侧阻抗很小,对系统的正常工作不产生影响。
当系统发生短路故障时,切断变压器的二次侧电流,停止磁通补偿,此时接入到电网中的变压器阻抗为一次侧阻抗和励磁阻抗。由于励磁阻抗较大,可以在发生短路故障时限制短路电流大小。变压器的等效模型如图3所示。

图3 停止磁通补偿时变压器等效电路
1.2 工作电路模型
利用空间矢量(SVPWM)控制技术控制逆变器产生一个可以跟踪变压器一次侧电流相位的电流,其幅值和一次侧电流的幅值的关系为k˙I2X=-˙I1,其中k为变压器的变比。将逆变器产生的电流注入到变压器的二次侧就可以将变压器的磁通补偿为零。工作电路拓扑图如图4所示。
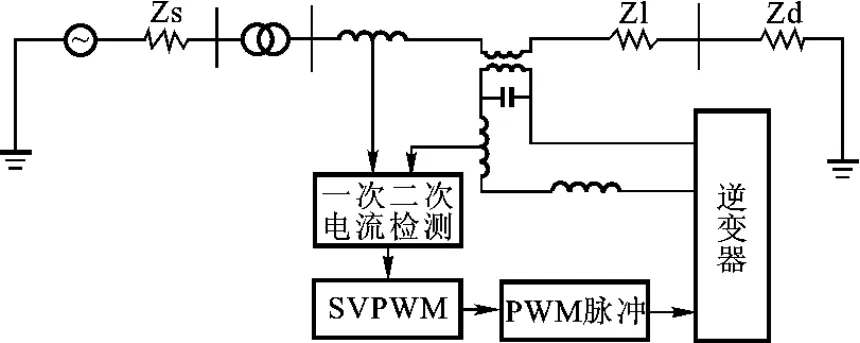
图4 短路电流限制器工作电路拓扑图
以单相为例,将变压器的一次侧电流即系统电流和变压器二次侧电流即由逆变器产生的跟踪电流进行采样取值,经过处理变为SVPWM的信号指令,产生的PWM脉冲控制逆变器工作。
2 基于SVPWM的控制方法设计
2.1 零磁通短路电流限制器数学模型
零磁通短路电流限制器由逆变器电路产生跟踪电流,将逆变器作为控制对象,控制量为变压器一次侧的系统电流和注入变压器二次侧的跟踪电流。零磁通短路电流限制器的拓扑结构图[2-4]如图5所示。
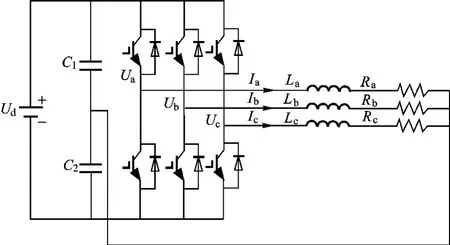
图5 逆变器拓扑图
根据图5的电路拓扑结构图,由基尔霍夫电流定律可得到如下状态方程:

通过坐标变换得到两相旋转坐标系d、q坐标下的逆变器数学模型,即

式中,ω为系统电压的角速度;Id、Iq为电流的d、q轴分量;Ud、Uq为电压的d、q轴分量;L为滤波电感感值,R为变压器和逆变器的等效电阻。
2.2 最优控制方法
2.2.1 线性最优控制(MATLAB)
由式(2)可以得到系统的状态方程为

其中
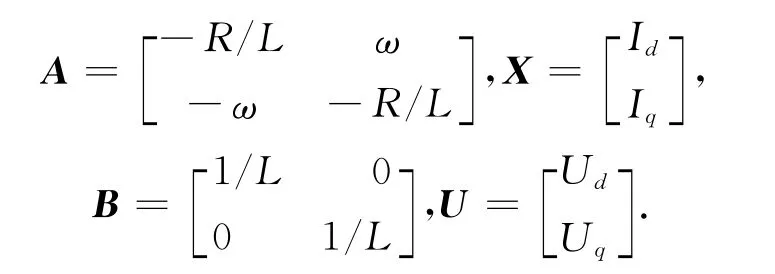
将式(3)所示的状态方程偏差化可得
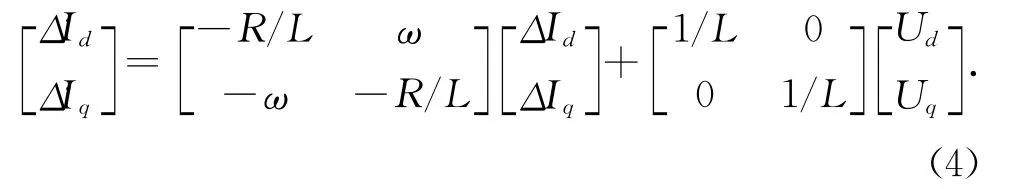
根据最优控制原理,性能指标选择为二次型指标
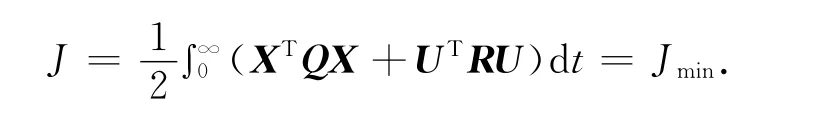
所需求取最优反馈增益矩阵为
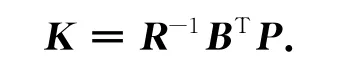
其中P为黎卡堤方程
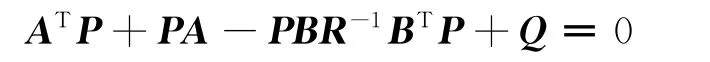
的解,而且P是2×2的矩阵。
那么最终得到的最优控制规律为
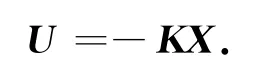
根据权矩阵Q的取值不同,求解黎卡堤方程得到的P也不同,因此形成的最优控制规律也不同。
2.2.2 非线性最优控制(SIMULINK)
令x1=ΔId,x2=ΔIq,那么式(4)所示的状态方程可以变为
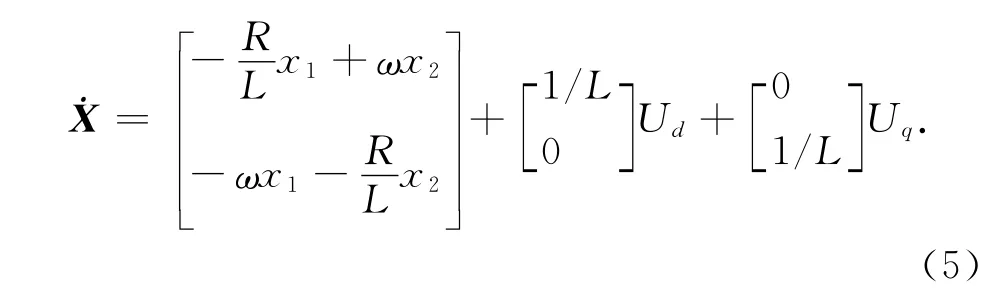
其中

(1)计算系统的指标数。因为系统的输入量个数m=2,状态变量个数为n=2,那么取m=n1=2,这样为了满足,取n2=0,则N=2。那么,组成2个向量场的集合为
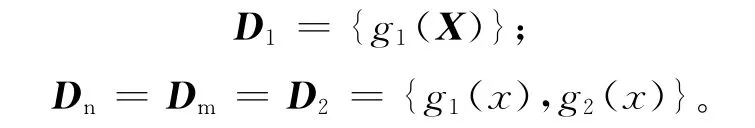
(2)选择最简单的n=2个线性独立向量场。则
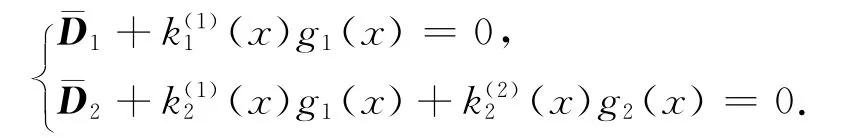


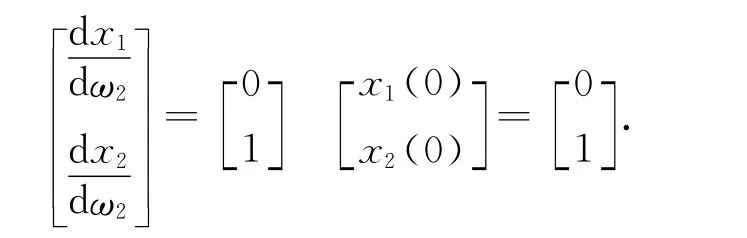
由此可以求出
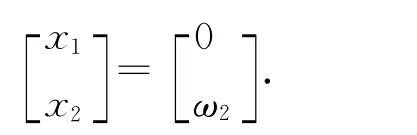

由此可以求出

即所求映射为

则其逆映射关系为
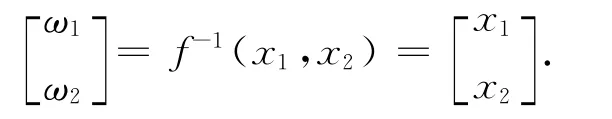
(4)求解f(0)(ω),为此先求取F-1的雅克比矩阵,即

则
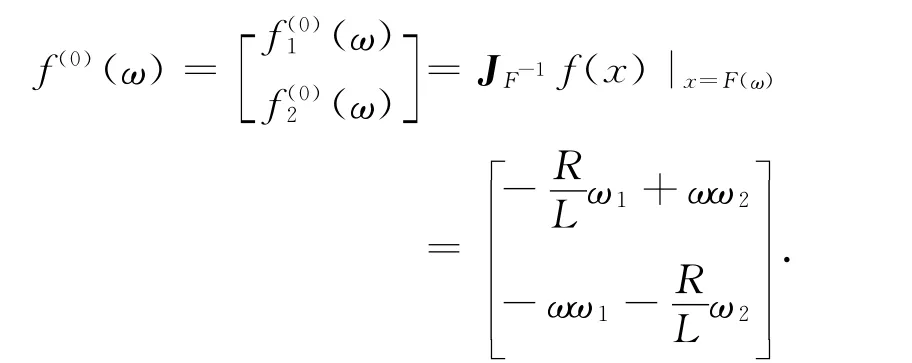
因为系统的N=2,只需求变换RN-1=R1:
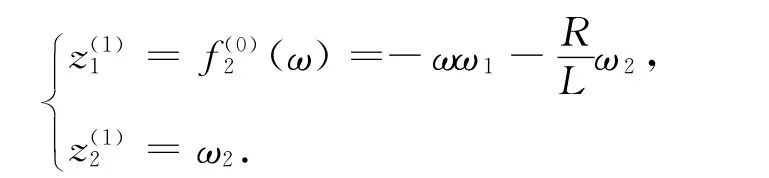
相应地,变换T=R1F-1应为

T的雅克比矩阵为
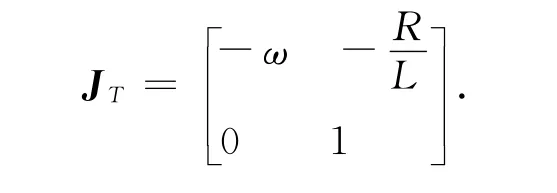
由变换T可以求出最后一组变换为

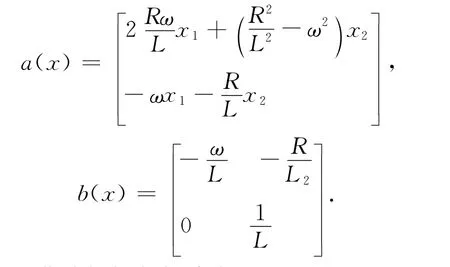
则该系统非线性控制规律为
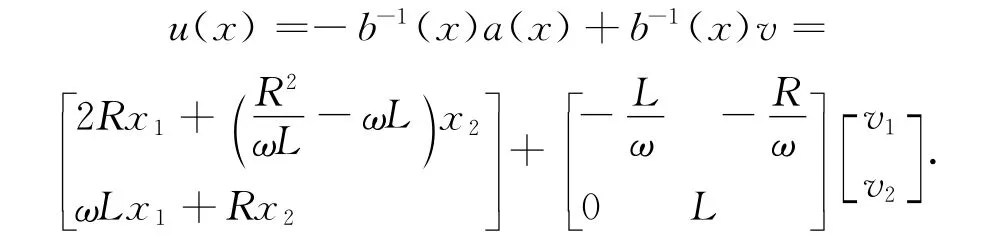
令
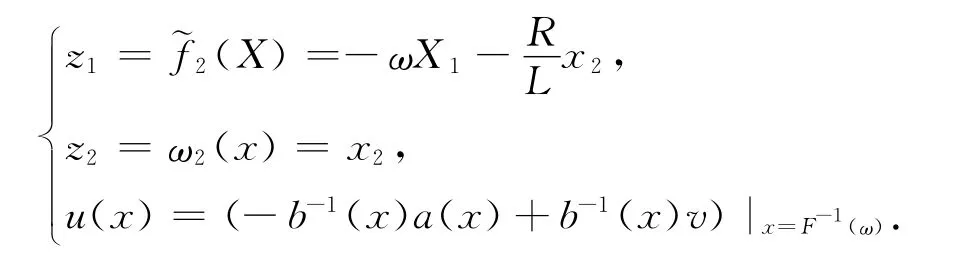
则原系统已被精确线性化为以下的布鲁诺夫斯基标准型
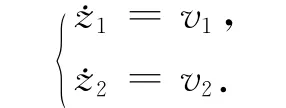
所需求取最优反馈增益矩阵为

其中P为黎卡堤方程
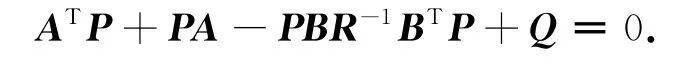
的解。可以求得最优控制规律v*为

那么最终的控制规律为
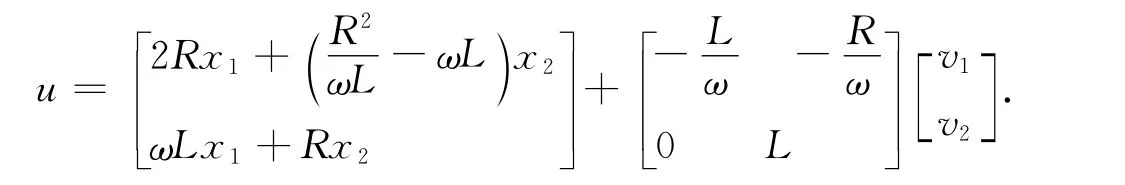
权矩阵Q的取值不同,形成的最优控制规律也不同。



当时,

3 仿真结果
在 MATLAB/SIMULINK环境下搭建基于SVPWM控制零磁通短路电流限制器的仿真模型并进行仿真分析[5-6]。
以下是系统仿真参数:电感为1×10-4H,电阻为0.001Ω频率为50Hz,线路首端电压为6.3kV,下一级负荷额定电压为6.3kV,下一级负荷有功功率为1.2MW,线路阻抗为3Ω。
通过图6的比较可以看出基于零磁通的短路电流限制器的作用明显,在0.04s时发生短路故障,短路电流限制器迅速动作,将短路电流限制到原来短路电流水平的一半。
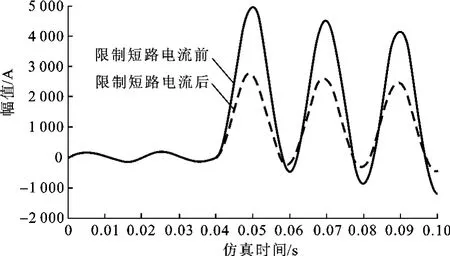
图6 短路电流波形对比
线性最优控制下跟踪电流波形对比如图7所示。注入到变压器二次侧的电流紧跟随流过变压器一次侧的系统电流变化,因此满足磁通补偿的条件,此时,接入系统中所呈现的阻抗仅为变压器一次侧阻抗,不影响系统的正常工作。
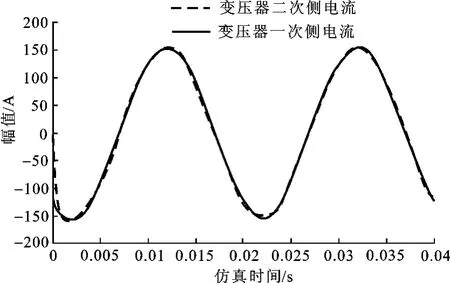
图7 线性最优控制电流跟踪对比
非线性最优控制下跟踪电流波形对比如图8所示。

图8 非线性最优控制电流跟踪对比
采用非线性最优控制的电流跟踪效果比较差,原因是该系统本身是线性系统,当采用非线性的控制方法之后,反而将控制变得更加复杂,效果反而不好。
4 结束语
利用空间矢量控制的方法可以产生跟踪效果较好的磁通补偿电流进行磁通补偿。基于SVPWM的零磁通短路电流限制器在发生短路故障时,可以有效地限制短路电流的水平。
[1]魏亚南,陈乔夫,李达义,等.基于磁通补偿的故障电流限制器[J].电力系统自动化,2003,27(14):42-44.
[2]康忠健,陈天立,訾淑伟,等.不平衡电网下三相PWM整流器控制策略的研究[J].控制理论与应用,2010(8):1097-1102.
[3]史威.三相逆变器SVPWM调制研究[D].武汉:华中科技大学电力学院,2011:90-98.
[4]叶盛,黄守道,黄科元,等.不对称电压下PWM整流器的控制策略[J].电网技术,2010,10(10):37-42.
[5]张加胜,张磊.电力电子技术[M].东营:石油大学出版社,2004:108-115.
[6]张润和,崔丽丽.基于 MATLAB空间矢量脉宽调制方法[J].辽宁工程技术大学学报,2004,23(6):793-795.

