神经网络动态规划在溶解氧控制中的应用

薄迎春，李来鸿，马善鹏，夏伯锴

(1.中国石油大学信息与控制工程学院，山东 青岛 266580，2.胜利油田河口供电公司，山东 东营 257200;3.山东石大科技集团有限公司，山东东营 257062)

溶解氧质量浓度控制对于采取活性污泥法的污水处理过程有着重要意义［1-3］。溶解氧质量浓度过低，使污泥活性降低，会抑制生物对有机物的降解，产生污泥膨胀。溶解氧质量浓度过高会加速消耗污水中的有机物，使微生物因缺乏营养而引起活性污泥的老化，增加能耗［3］。目前，实际溶解氧质量浓度控制主要采取PID控制策略［3］。由于污水处理过程非线性较强，其入水流量、入水污染物质量浓度等时刻发生变化，固定参数的PID控制器难以取得好的控制效果［2］。近年来，模型预测控制在污水处理过程得到了广泛的应用［2-3］。但是，由于污水处理过程参数的时变特性及不确定性，目前的机制模型在应用过程中很容易出现模型失配现象［2-3］。针对一类模型难以确定的被控过程，数据驱动控制方法在近几年得到了一定的重视［4-6］，其最大的优点是控制器的设计过程可以直接通过对输入、输出数据的学习实现控制器参数的调整。神经网络动态规划控制(neural dynamical programming control，NDPC)是一种典型数据驱动的控制方法［4］。该方法以Bellman优化原理为基础、采用神经网络逐步逼近系统最优的控制策略［7-8］。针对污水处理过程的溶解氧质量浓度控制问题，笔者提出一种NDP控制方案，并对评价网络的收敛性进行分析。

1 神经网络动态规划原理

一般的优化问题均设定一性能指标函数，优化实质是使该性能指标达到最大或最小。其形式［8］为

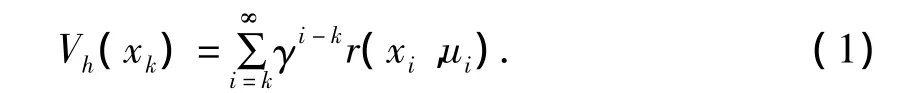
式中，Vh(xk)为优化问题的回报函数;r(xi，ui)为立即回报或当前回报;0＜γ≤1为回报因子;xk为系统的状态;uk为控制策略。式(1)也可写为

该方程也称为Bellman方程，为方便起见，Vh(xk)简记为 Vk，r(xk，uk)简记为 rk。令

Ek称为TD(time difference)误差［8］。下一步的最优行动［8］为

如果被控对象模型已知，通过求解式(4)即可得到下一时刻的最优控制策略。然而，在污水处理过程中系统的数学模型很难建立，所以用解析的方法难以获得式(4)的解。NDPC采用迭代方法逐步逼近最优的评价函数及最优的策略，从而避免了需要建立系统数学模型的缺陷。其结构如图1所示。

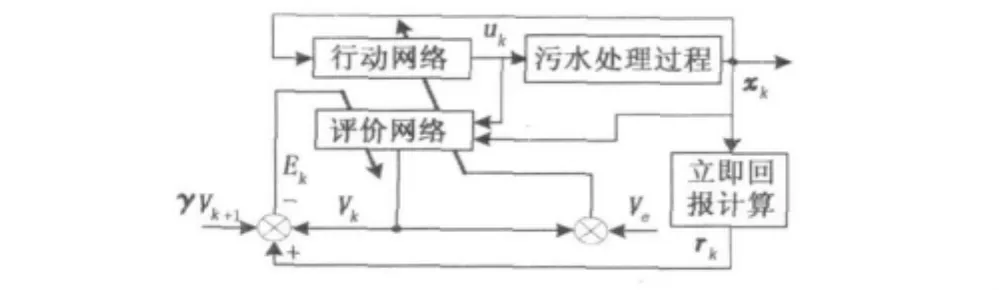
图1 神经网络动态规划控制器结构框图Fig.1 Frame of NDPC

NDPC一般由两个神经网络实现。其中，评价网络的作用是对当前的控制策略进行评价，其输出为当前控制策略的评价值Vk;而行动网络以评价网络得出的评价值为依据确定下一步的控制策略。策略评价及策略优化过程在与系统交互的过程中交替进行。

2 神经网络动态规划控制器设计

NDPC的设计过程实质上是评价网络和行动网络的参数调整过程。本文中，评价网络及行动网络均采用 ESN［9］。

2.1 ESN简介

ESN是一种递归神经网络，目前已经在时间序列预测、系统辨识等领域得到了广泛的应用［9-11］。在不考虑输出到内部状态反馈的情况下［12］，其数学形式为

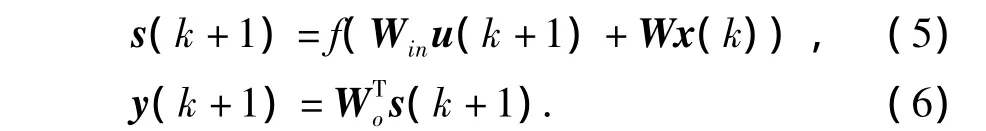
式中，u(k)=［u1(k)，…，uK(k)］T为网络输入;s(k)=［s1(k)，…，sN(k)］T为内部状态;y(k)=［y1(k)，…，yL(k)］T为网络输出;Win、W分别为输入及内部状态的连接权值矩阵，维数分别为N×K，N×N，K为输入维数，N为内部神经元个数;Wo为内部状态到输出的连接权值矩阵，维数为L×N，L为输入维数;f为内部神经元激活函数。W及Win均在学习之前确定，并且在学习和测试过程中保持不变，即ESN的学习只需确定Wo的值［11］，这降低了神经网络训练的复杂性，同时保持了神经网络的递归特性。

2.2 评价网络的在线学习

对于评价网络，其输出为当前策略下的评价值Vk。在每一时刻k，评价网络的训练目标为

这里，j为迭代步数，对于每一时刻的行动uk，评价网络需经过多次学习，直到Ek(j)＜ε，ε为一很小的正数。所以，评价网络的性能指标可设为

按照梯度下降算法，评价网络的权值修正量为

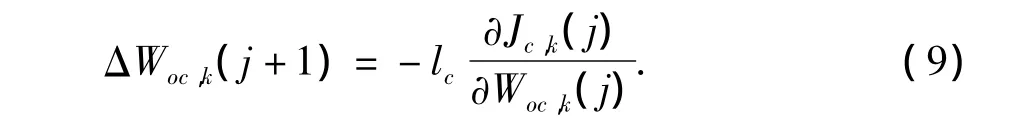
式中，lc为评价网络的学习率。将式(8)代入式(9)得

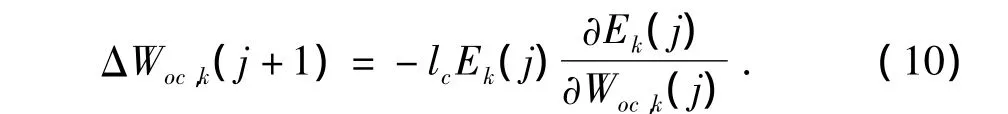
将式(3)代入式(10)可得

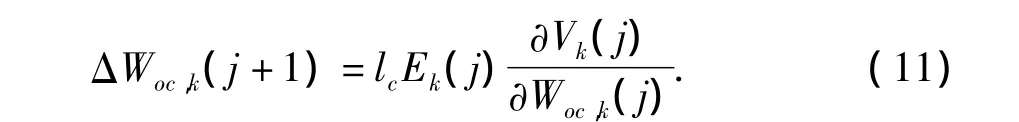
根据式(6)，有

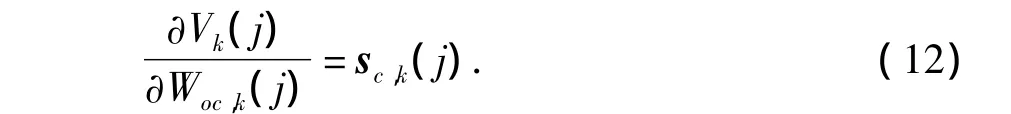
所以，

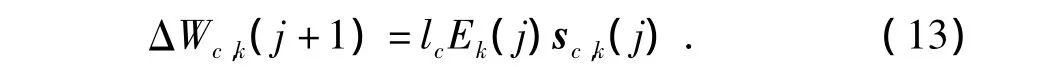
2.3 行动网络的在线学习

控制网络的学习目标是选择合适的控制策略，使评价网络的输出Vk逐渐接近最终期望的回报Ve，控制网络的学习目标可以设置为

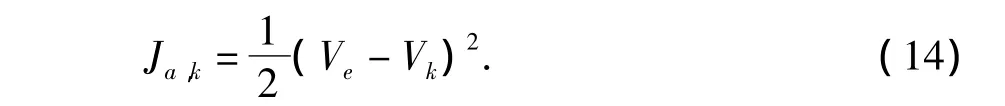
应用梯度下降算法

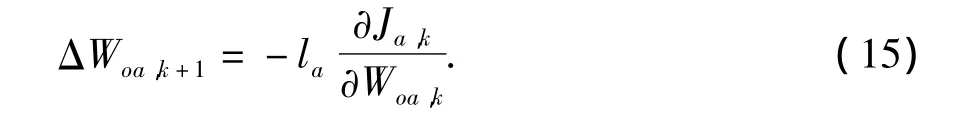
式中，la为控制网络的学习率，根据链式求导法则

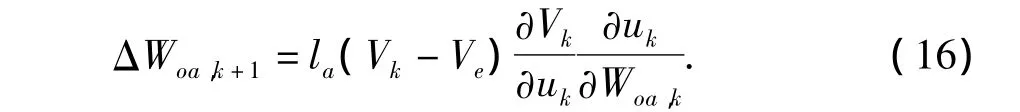
根据公式(6)，有

应用链式求导法则，

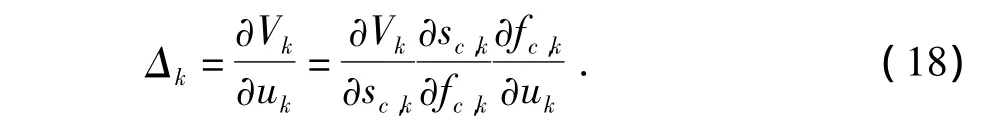
式(18)的各项可以通过评价网络求解。由此可以得出行动网络的权值修正量为

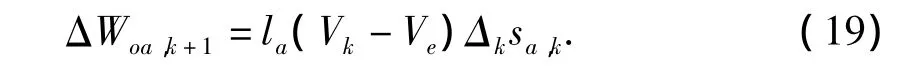
3 试验分析

3.1 立即回报的确定

BSM1模型［13］定义了几种回路级控制的性能评价指标，其中最重要的是方差积分ISE和控制量方差σ(u)，其形式如下:

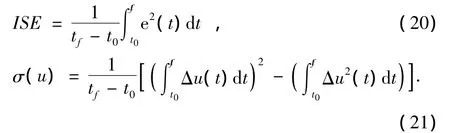
ISE及σ(u)主要反映了系统的控制精度及控制量的波动。对于一个跟踪控制过程，控制精度是首要追求的目标，此外，在系统平稳运行时也不希望控制量出现大幅的波动。与控制精度指标相关的立即回报可定义为

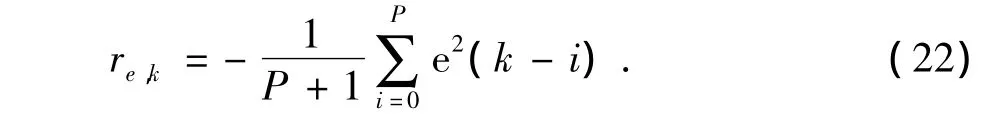
re，k反映了过去一段时间内被控量的均方误差。P是回退时间步数，选取误差平均值是为了避免当前偏差存在严重干扰时引起的评价不准。类似地，与控制量相关的立即回报可定义为

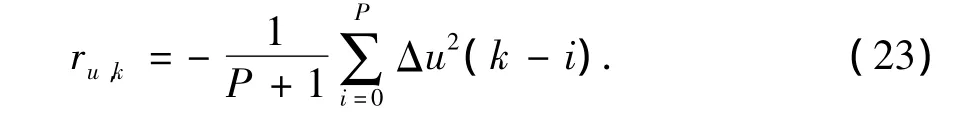
系统总的立即回报可定义为

其中 β1、β2为权重系数，β1+ β2=1。

3.2 仿真试验

BSM1模型中包含了干燥天气、雨天以及暴雨天气下的三个入水文件［13］，为了测试神经网络动态规划控制器的性能，取干燥天气的第1、2、3天的数据，雨天第10、11天的数据以及暴雨天第8、9天的数据，并将这7天的数据集合作为入水流量数据。这样可以体现入水流量的多样性变化。污水处理的最终目标是使出水指标满足标准，所以控制精度是首要考虑的指标，取β1=0.9，β2=0.1。根据立即回报的形式，可以得出期望的最大回报Ve=0，γ取为0.2。首先，溶解氧的设定值设为2 g/m3，并保持不变，NDPC及PID控制器的控制效果如图2所示。由图2可见，NDPC控制器作用下，溶解氧质量浓度保持在1.98～2.02 g/m3，波动幅度约为 ±1%，而PID控制器作用下，溶解氧质量浓度为1.92～2.05 g/m3，波动幅度约为±8.5%。

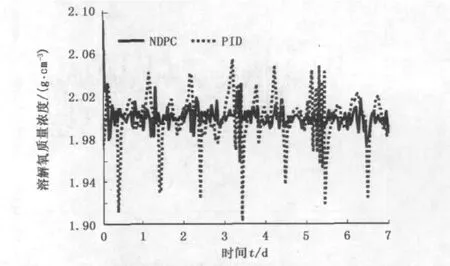
图2 入水变化时NDPC和PID控制器跟踪曲线Fig.2 Tracking circles of NDPC and PID controller

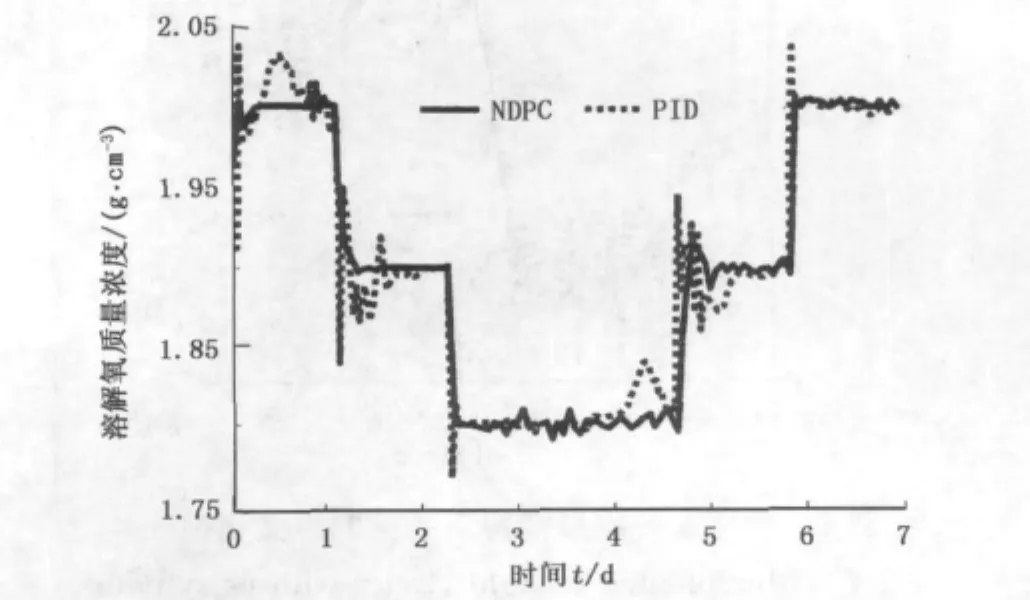
图3 设定值变化时NDPC和PID控制器跟踪曲线Fig.3 Tracking circles of NDPC and PID with varying set points

图3显示了NDPC及PID在溶解氧质量浓度设定值变化情况下的跟踪情况，两种控制器在跟踪的快速性上相当，但是，NDPC的跟踪精度明显高于PID控制器。这两个试验表明NDPC对不同的输入变化具有较好的适应性，能够在较大程度上提高控制精度。

鲁棒性是衡量控制器性能的重要指标。由于NDPC本质上是一种数据驱动的控制器，在整个控制器的设计过程(或参数自适应调整过程)中，只是以系统的输入、输出数据作为设计控制器的依据，并未考虑系统的动力学模型，同时污水处理过程的动力学模型也是很难确定的。所以，基于模型的传统鲁棒性分析方法不再实用［4］，而数据驱动理论发展还远未完善［4-6］。在实践中普遍认为，数据驱动控制器对噪声数据的适应能力可以作为控制器鲁棒性的一个衡量标准。所以，试验中将BSM1模型中所有检测的物理量按照BSM1的约定的传感器类型加入相应的干扰［13］。取干燥天气第1天的数据进行测试，结果如图4、5所示。

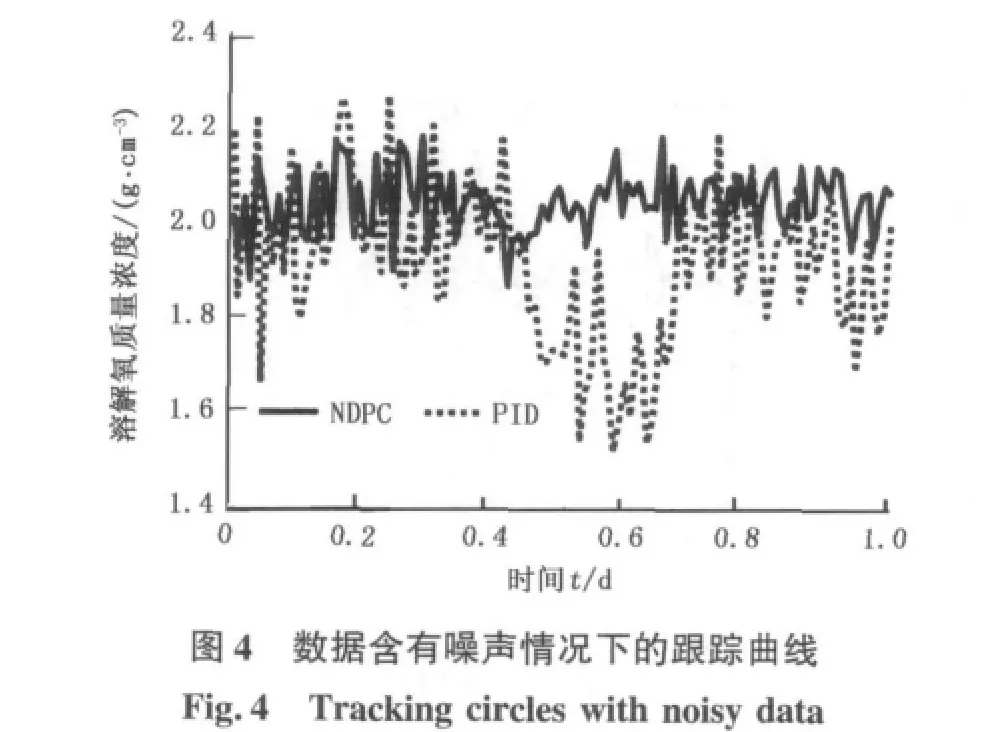
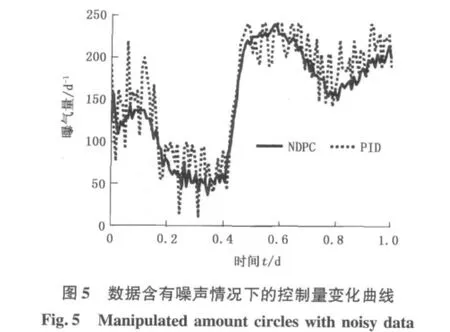
图4为溶解氧质量浓度的变化曲线，图5为控制量变化曲线。由图4可见，NDPC控制下的溶解氧质量浓度波动(1.89～2.19 g/m3)远小于PID控制器作用下溶解氧的波动(1.57～2.25 g/m3)，说明NDPC对噪声也有较好的适应能力，即NDPC具有较好的鲁棒性。同时，从图5也可以看出，NDPC的控制量波动也明显减弱，控制过程更为平稳。

表1为PID控制器与NDPC的部分底层控制性能指标［13］对比。表2为两种控制器作用下的出水质量指标的变化情况。从表1、2可以看出，由于控制器的鲁棒性增强，NDPC的各项底层控制性能均优于PID控制器。此外，由于控制精度的提高，NDPC的总体出水指标也比PID有所提高，尤其是脱氮能力得到增强。

表1 控制器性能对比Table 1 Performance of oxygen controllers

表2 出水质量指标比较Table 2 Indices comparison of effluent quality g/m-3

3.3 模型分析

NDPC在采取下一步的行动之前，首先要进行回报值的逼近，即对当前的控制策略进行评价。所以准确的评价是下一步行动选择的关键。在试验中发现，评价网络收敛速度对控制性能影响较大，而评价网络的学习率与其收敛速度密切相关。当学习率lc较小时，评价网络能够收敛，但收敛速度较慢;当学习率lc较大时，评价网络则可能会不收敛。所以确定学习率的选择范围对NDPC的控制性能非常关键。

引理1 设ESN没有输出反馈，内部神经元激活函数f为sigmoid类型函数，则当时，ESN是内部状态稳定的。

证明 设sk、s1，k分别为ESN的两个不同的内部状态，对于相同的输入uk+1，根据ESN的定义(式(5))有

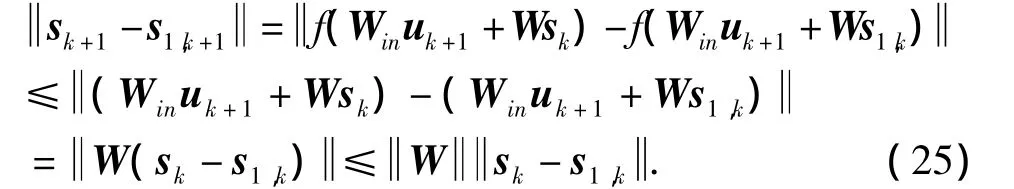
定理1 在评价网络内部状态稳定的情况下，若其学习率lc满足

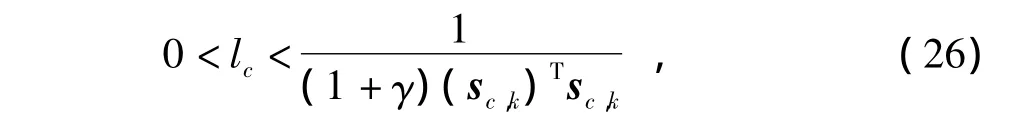
则评价网络是收敛的。

证明 设评价网络在输入uk下，sc，k的稳定状态为s*。即在ESN稳定的情况下，评价网络的训练步数足够大时，可以认为sc，k=s*。根据公式(3)，

Ek(j)是收敛的，即当 j→∞时，Ek(j)→0，求解式(33)可得

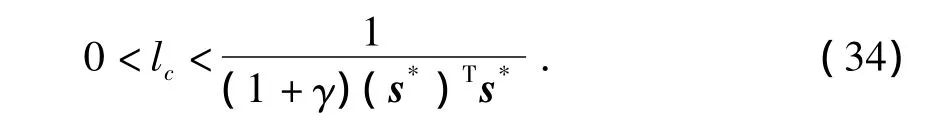
当j较大时，可以用 sc，k近似地代替s*，这样式(34)即变成式(26)，问题得证。

由于评价网络内部状态会随时间变化，所以可以采用满足式(26)的变化的学习率，这样既可以使神经网络保持稳定，又可以加快学习的速度。评价网络部分输出权值随学习率的变化情况如图6所示。其中

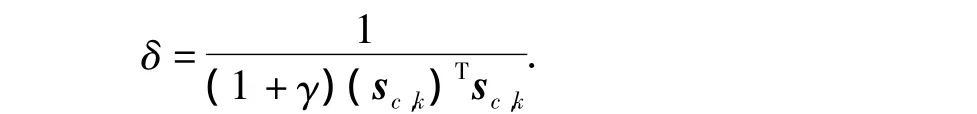
由图6可见，当lc＞δ时，评价网络的权值发散，而lc＜δ时，评价网络的权值收敛，而当lc=δ时，评价网络的权值处于等幅震荡状态。

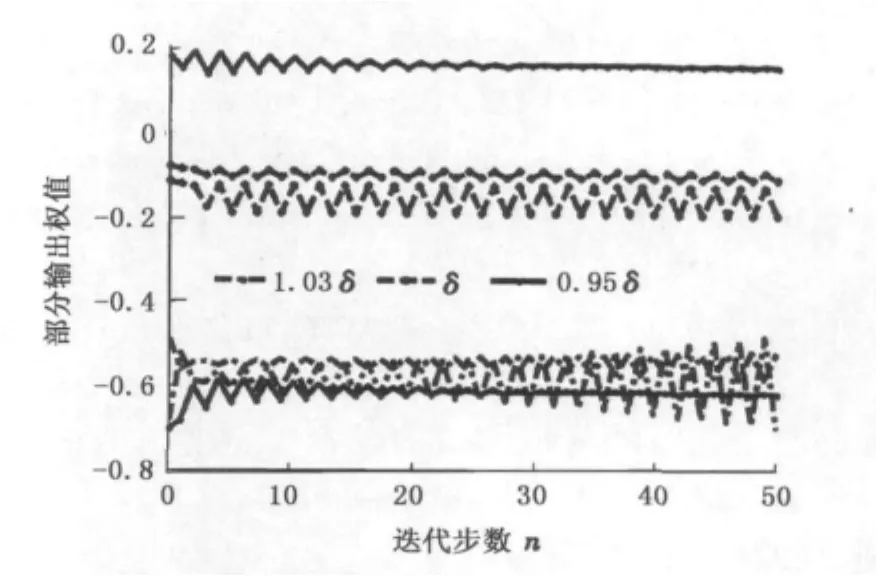
图6 不同学习率时评价网络可调权值变化Fig.6 Tunable weights changing with different learning rates

4 结束语

将神经网络动态规划方法应用在污水处理过程溶解氧质量浓度的控制中，与PID控制器的对比研究表明，NDPC在控制精度及鲁棒性等方面优于PID控制器。NDPC采用了数据驱动的控制模式，采用离线和在线的输入、输出数据对控制器参数进行自适应调整，避免了需要建立系统动力学模型的难题。对基于ESN的NDPC评价网络的收敛性进行了理论分析，给出了保证评价网络收敛的学习率选择范围，对合理选择学习率有一定的参考价值。

［1］ 刘春英，袁存光，郭继香.用吸附法处理石油污水中化学耗氧量的实验研究［J］.石油大学学报:自然科学版，2003，27(3):88-91.LIU Chun-ying，YUAN Cun-guang，GUO Ji-xiang.Experiment on disposal of chemical oxygen demand in petroleum wastewater by adsorption in seprpentine-Ni(NO3)2-H2O2system［J］.Journal of the University of Petroleum，China(Edition of Natural Science)，2003，27(3):88-91.

［2］ BRDYS M A，GROCHOWSKI M，GMINSKI T.Hierarchical predictive control of integrated wastewater treatment systems［J］.Control Engineering Practice，2008(16):751-767.

［3］ HOLENDA B，DOMOKOS E，REDEY A.Dissolved oxygen control of the activated sludge wastewater treatment process using model predictive control［J］.Computers and Chemical Engineering，2008(32):1270-1278.

［4］ XU J X，HOU Z S.Notes on data-driven system approaches［J］.Acta Automatica Sinica，2009，35(6):668-675.

［5］ HOU Z S，XU J X.On data-driven control theory:the state of the art and perspective［J］.Acta Automatica Sin-ica，2009，35(6):650-667.

［6］ WANG H，CHAI T Y，DING J L.Data driven fault diagnosis and fault tolerant control:some advances and possible new directions［J］.Acta Automatica Sinica，2009，35(6):739-747.

［7］ ERNST D，GLAVIC M，CAPITANESCU F.Reinforcement learning versus model predictive control:a comparison on a power system problem ［J］.IEEE Transactions on Systems，Man，and Cybernetics-part B:Cybernetics，2009(39):517-529.

［8］ LEWIS F L，VRABIE D.Reinforcement learning and adaptive dynamic programming for feedback control［J］.IEEE Circuits and Systems Magzine， Third Quater，2009，32-50.

［9］ JAEGER H.The"echo state"approach to analysing and training recurrent neural networks［R］.GMD Report German National Research Center for Information Technology，2001，12(8):1-43.

［10］ MUSTAFA C O，XU D M，PRINCIPE J C.Analysis and design of echo state networks［J］.Neural Computation，2007(19):111-138.

［11］ JAEGER H.Harnessing nonlinearity:predicting chaotic systems and saving energy in wireless communication［J］.Science，2004(304):78-80.

［12］ JAEGER H.Short term memory in echo state networks［R］.Technical Report GMD Report 152，German National Research Center for Information Technology，2002.

［13］ ALEX J，BENEDETTI L.Benchmark simulation model No.1(BSM1)［S］.IWA Taskgroup on Benchmarking of Control Stategies for WWTPs，April 2008.