基于Preisach滞后模型的地面沉降预测分析

吴 蓉，李成柱

（1.河海大学文天学院，安徽 马鞍山 243031；2.西安地质调查中心，陕西 西安 710054）

地面沉降是大多数平原城市已经面临或具有潜在隐患威胁的一种城市地质灾害。其发生的原因在于随着城市的发展需要开采大量的地下水，直接导致地层的承载力下降而引起的。且地面沉降的发生直接造成了城市的地质环境质量降低，给城市建设和发展带来了危害。地面沉降是一种缓变型的城市地质灾害，具有累进性特点。为了防治城市地面沉降问题，以抽水引发的地面沉降的模拟和预测一直是国内外相关专家研究的重点和热点。目前，抽水引起的地面沉降预测模型主要以渗流场和应力场的部分耦合或完全耦合模型为主，但是渗流场和应力场完全耦合的地面沉降模型，需要的参数多且不易确定，导致模型应用难度较大。因此，不需要研究地面沉降机理，只需要知道沉降与时间关系的生物预测模型得到了研究者的关注。抽水引起的地面沉降明显存在滞后效应，且其含水层水位变化与地层变形之间是一种非线性关系。1935年，Ferenc Preisach提出Preisach模型，来描述铁磁材料中的迟滞数学模型。目前，Preisach模型是电磁学、控制应用理论中应用最为广泛的一种迟滞非线性模型，还没有发现Preisach模型在地面沉降方面的应用。本文正是借助于Preisach模型的滞后非线性特点对抽水引起的地面滞后性沉降进行模拟和预测。

1 Preisach模型

Preisach模型可以看作是一系列带有权重的迟滞单元叠加的结果［1］，即

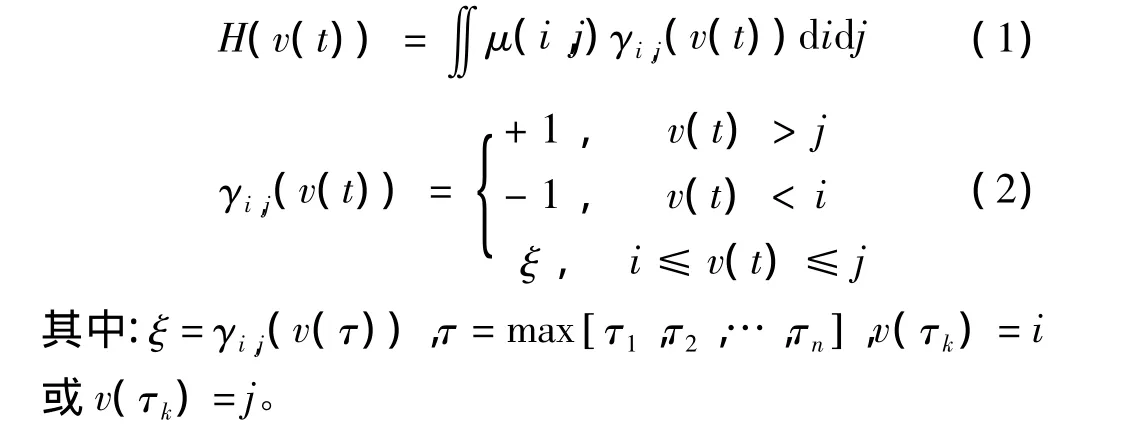
式中:μ(i，j)——权重函数；

γi，j(v(t))——Preisach 模型的迟滞单元；

i——表示迟滞单元的上切换值；

j——表示迟滞单元的下切换值。

为了减少模型误差，G.Webb对 Krasnosel's和Pokrovskii提出了KP迟滞模型。为了得到参数化迟滞模型，G.Webb对连续KP模型的积分区域S进行均匀离散化，得到离散化的KP模型［2］为:

式中:n——积分区间 [ vmin，vmax]的离散化点数；

ξs——记忆单元，它随着 v( t)的符号进行变化。

式(3)～(5)即为参数离散化Preisach滞后模型，运用在地面沉降预测时，根据历史水位、沉降量和当前的水位确定当前的沉降量。Preisach模型的权重函数μi，j可以用分布函数代替［3］，如高斯函数等。高斯密度函数的表达式为:

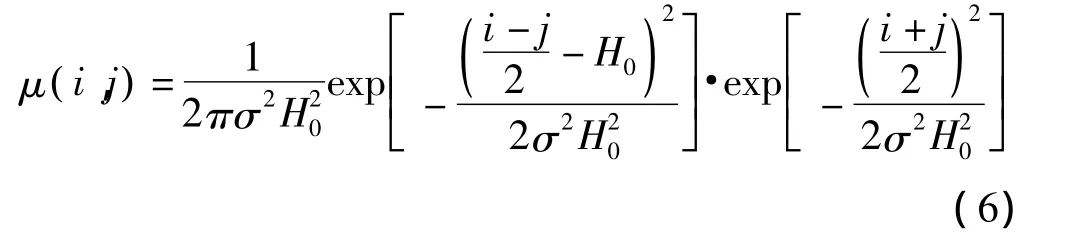
式中:H0——平均临界值；

σ——标准偏差；

H0、σ——待识别参数。

2 实例计算

利用上述模型对地面沉降进行预测，实验数据来自某地10年间75个时间点的地面沉降量与水位观测数据，如图1所示。为了满足模型的要求，对前7年共计53个原始数据进行了处理，首先将沉降量和水位通过插值方法得到等时间间隔的64个数据点，再将累计沉降量转换成一次观测的沉降量并与水位数据规范到［－1，1］区间，处理结果见图2所示。

图1 原始累计沉降量及水位变化图Fig.1 Change in land subsidence and groundwater levels

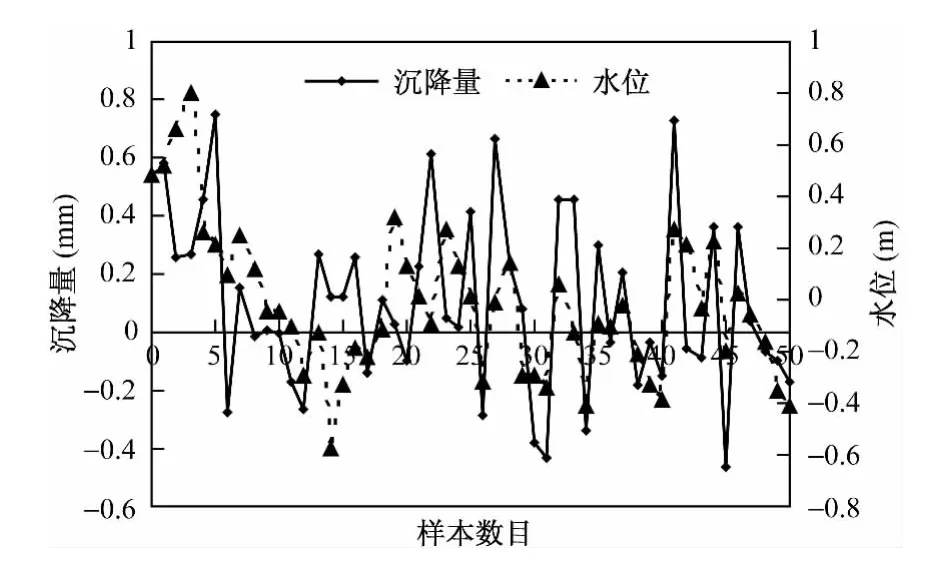
图2 规范后沉降量及水位变化图Fig.2 Chang in standard land subsidence and groundwater levels

为了检测模型的效率及准确性，采用6组不同数量的数据进行沉降量预测值的校验。6组不同数量的数据样本分别是前7年时间段内15个、30个、50个数据，前两个数据2个样本空间，共计5组数据。当沉降量和水位时间间隔不等时，可通过插值方法得到等时间间隔的数据，为了便于比较，5组数据统一预测的时间段为最后3年，以最后22个数据为测试依据。将5组数据代入到公式(3)～(6)中，采用模拟退火算法得到5组H0、σ值，结果见表1。并将得到的拟合结果和预测结果与实测值进行对比，结果见表1和图3～4。

表1 Preisach模型参数值Table 1 Parameters of Preisach model

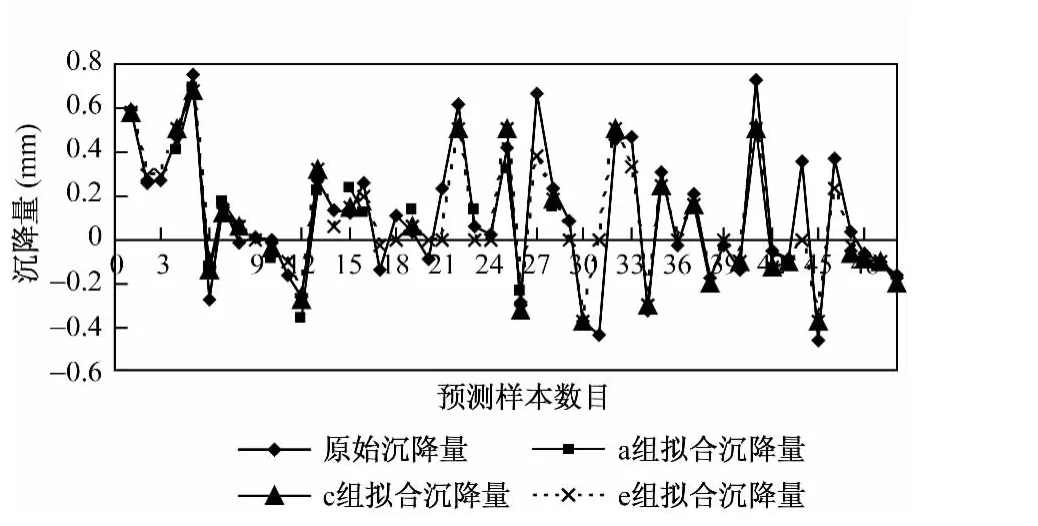
图3 拟合数据与实测数据比较图Fig.3 Comparison curve of modeling data and real data

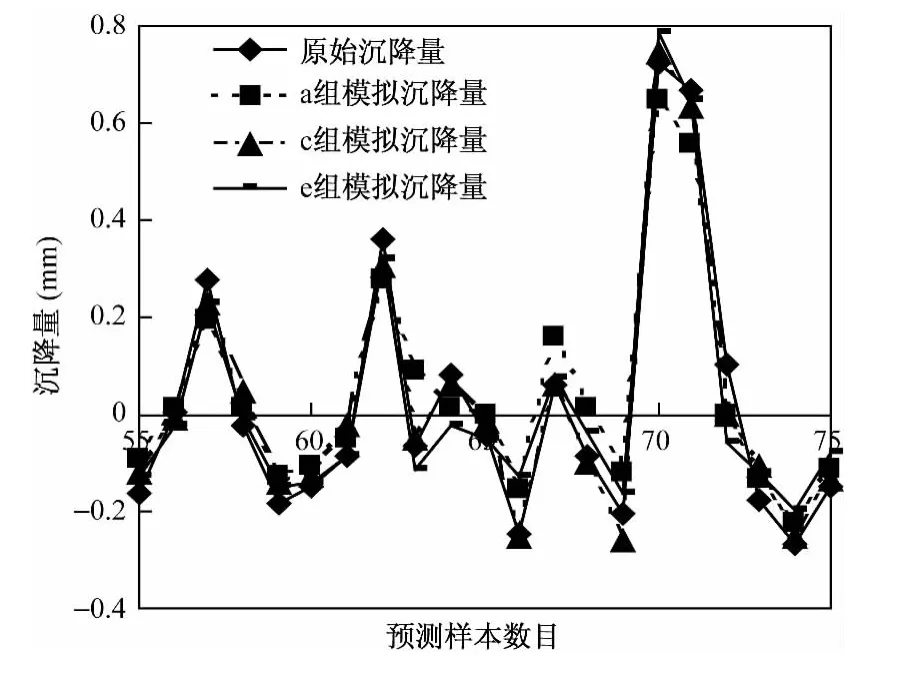
图4 预测数据与实测数据比较图Fig.4 Comparison of prediction data and real data

从表1和图3～4可以看出数据样本越多，平均相对误差有越小的趋势；同时表1中d组、e组的相对误差最小，表明不是样本越多平均相对误差越小。由图4和表1可以看出预测值的精度与所选样本空间相关，在前期拟合过程中样本拟合精度越高，后期预测的精度越高。所以Preisach滞后模型在沉降量预测方面的精度不仅与样本数量有关，同时与样本的质量有关。表1表明d组中Preisach滞后模型的模拟和预测曲线拟合十分理想。

为了说明Preisach滞后模型的可行性，针对此区域采用有限元方法模拟和预测了抽水引起的地面沉降。对比Preisach滞后模型和有限元方法得到的地面沉降的结果，由于此区域地层的物理力学性质不确定，在有限元方法反演水文地质参数和物理力学参数时，拟合的最小整体平均误差为6.21%，最终得到的沉降量预测值的整体平均误差为10.22%。从拟合和预测结果来看，Preisach滞后模型比有限元方法的误差更小，更接近实测值。

3 结论

抽水引起的地面沉降相对于抽水时间存在明显的滞后，并且这种滞后现象可以完全符合Preisach模型描述的滞后规律。研究表明，将不需要研究地面沉降机理的预测模型Preisach滞后模型应用到抽水引起地面沉降的模拟和预测方面是可行的。同时，Preisach滞后模型在沉降量预测方面的精度不仅与样本数量有关，同时与样本的质量有关。并不是样本的数量越多，预测模型的精度越高，而样本在时间上越没有规律，计算也越复杂。本文提到的Preisach滞后模型预测的地面沉降，当原始数据选择符合规律，模型具有预测精度高、所需参数少等优点，能很好地反映研究区域的地面沉降的变形趋势。

［1］Gorbet R B.Control of hysteretic systemswith Preisach representations［M］.Canada:Publishing House of University of Waterloo，1997.

［2］GE P，Jouaneh M.Generalized Preisach model for hysteresis nonlinearity of piezoceramic actuators［J］.Precision Engineering，1997，20(2):99 －111.

［3］Henze O，Rucker W M.Identification procedures of Preisach model［J］.IEEE Transactions on Magnetics，2002，38(2):833 －836.