塑性混凝土弹性模量的计算方法

李 杨

（郑州大学 新型建材与结构研究中心，郑州 450002）

塑性混凝土由粘土、膨润土和水泥等胶凝材料，砂子和石子等骨料，粉煤灰和矿渣等掺合料，减水剂和引气剂等外加剂，经加水拌合后搅拌、浇筑、凝结与硬化而形成的一种复合柔性工程材料，其弹性模量的室内测试没有现行规范，试验要求基本参照普通混凝土试验规程，由于其变形性能有别于土和普通混凝土，故完全采用普通混凝土或土的弹性模量测试方法存在较多问题［1］.本文归纳了近期塑性混凝土弹性模量测试方法的研究成果，并对弹性模量计算方法进行探讨，结论可为塑性混凝土材料相关规范制定和配合比设计提供参考.

1 近期研究成果

塑性混凝土弹性模量试验方法与普通混凝土弹性模量试验方法相似，但是在预加载、加载速率、测量标距和割线点的截取范围等方面稍有不同.付超云等认为对一定强度的塑性混凝土，存在一个加载速率范围，在这个范围之内，塑性混凝土强度和峰值应变受加载速率的影响较大［2］.王清友等认为塑性混凝土弹性模量试验宜采用位移控制，速率为0.2mm／min较为合适［3］.李家正等认为试件不需预压，但平均加载速率应控制在0.05～0.15MPa／s，同时试件的变形速率应维持在10－5／s.李清富等认为应先预压至相邻两次变形值相差不超过0.004mm，并控制加载速率在0.05～0.1MPa／s，采用300mm测量标距较为合适［4］.王四巍等认为测量标距减小，弹性模量值增大，试验不需预压且测量标距应取试件全长300mm，截取0.3倍、0.7倍峰值强度对应点割线斜率［5］.杨林等认为截取0.3倍、0.7倍峰值强度对应点割线斜率较好［6］.高丹盈等认为截取0.3倍、0.6倍峰值强度对应点割线斜率或0.45倍峰值强度对应点的切线斜率较好［7－8］.袁梅等认为截取0倍、0.4倍峰值强度对应点的割线斜率较好［9］.

综上，在塑性混凝土弹性模量测试上，研究者对弹性模量变形测量标距应为试件全长、试件不预压、采用作图法计算、取割线斜率、控制加载速率在0.05～0.15MPa／s范围内等问题已基本达成共识，但在割线点的选定上仍存异议.本文针对此问题，对塑性混凝土弹性模量的计算方法进行研究.

2 试验设计及计算方法

2.1 试验设计

试验采用原材料为:河南省卫辉市天瑞水泥厂有限公司生产的“天瑞”牌袋装P.O42.5级普通硅酸盐水泥；河南省信阳市平桥区广运膨润土有限公司生产的“广运”牌钙基一级膨润土；粗骨料为粒径5～20 mm的碎石；细骨料为天然河砂，细度模数2.3，属中砂，颗粒级配曲线位于Ⅱ区.原材料相关指标均符合规范要求.

采用强制式搅拌机拌合，人工插捣成型，在（20±5）℃的室内静置48h后拆模并移入标准养护室，养护至28d龄期后试验.试验在3000kN数显压力试验机上进行，试件尺寸为150mm×150mm×300mm，加载速率为0.1MPa／s，变形测量标距为试件全长300mm.塑性混凝土应力－应变关系曲线测试时，荷载和竖向变形分别采用荷载传感器和电子位移计量测，通过IMP数据采集仪自动采集.配合比设计和轴心抗压强度见表1.

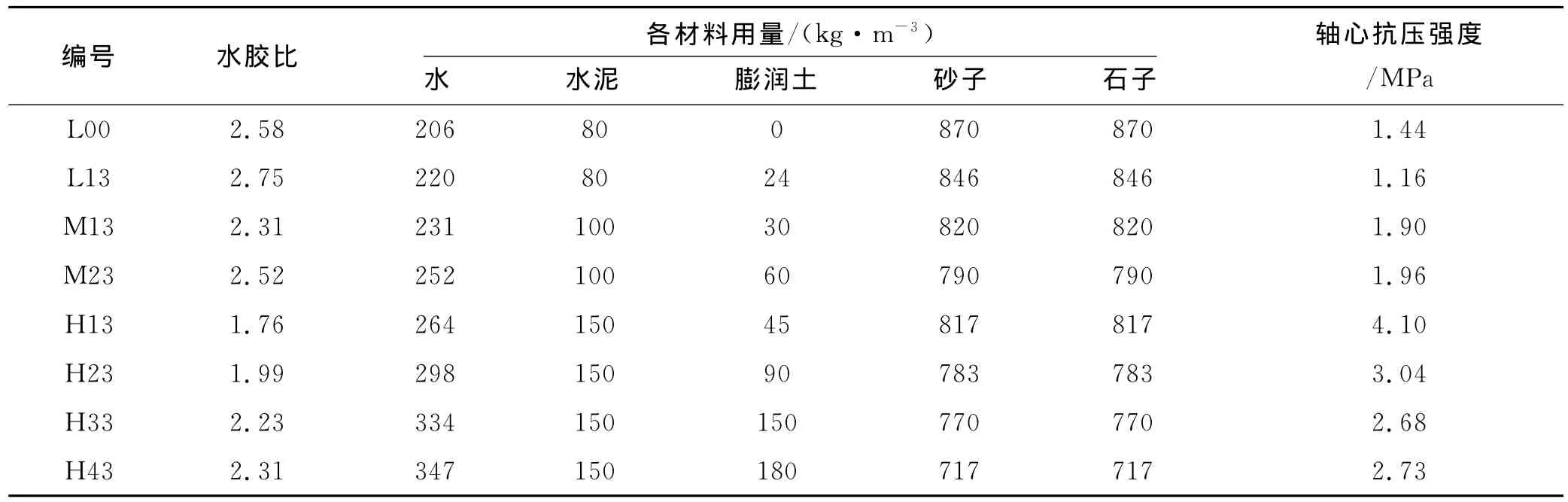
表1 塑性混凝土配合比设计及28d轴心抗压强度

2.2 试验方法

图1是实测塑性混凝土典型的无侧限受压应力－应变曲线.塑性混凝土弹性模量计算的难点是其受压时存在初始加载弯曲段OP1.初始加载弯曲段内，塑性混凝土试件被压密实［9］，受压应力－应变曲线斜率逐渐增大.随后直线段P1P2内，塑性混凝土应力－应变曲线斜率较为稳定，此时是计算其弹性模量值的最佳阶段.

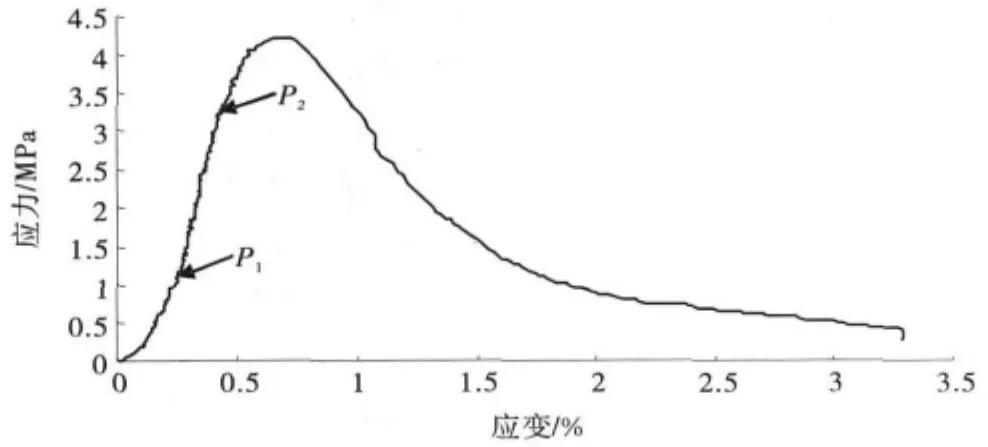
图1 塑性混凝土无侧限受压应力－应变全曲线

首先对实测塑性混凝土无侧限受压应力－应变曲线分析，发现其应力－应变曲线在约0.2倍、0.8倍峰值强度对应点之间呈较好的直线.根据曲线特点，猜测直线段起始点P1选取过小或终止点P2选取过大都会造成塑性混凝土弹性模量计算值的减小.结合近期研究成果，本次欲取直线段起始点P1分别为:0.2σ和0.3σ；直线段终止点P2分别为0.6σ、0.7σ和0.8σ.弹性模量值参照《水工混凝土试验规程》（DL／T5150－2001）按照公式1计算.

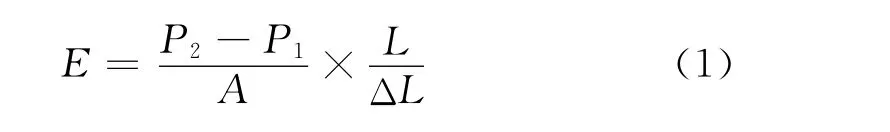
式中，E为弹性模量（MPa），根据P1和P2点的不同，弹性模量计算值编号分别为E26、E27、E28、E36、E37和E38；P1为直线段起始点荷载（N），分别为极限破坏荷载的0.2倍和0.3倍；P2为直线段终止点荷载（N），分别为极限破坏荷载的0.6倍、0.7倍和0.8倍；ΔL为应力从P1增加到P2时试件的变形（mm）；L为变形测量标距（mm）；A为试件承压面积（mm2）.

3 试验结果与分析

各组塑性混凝土配合比的6种弹性模量计算值列于表2.计算结果表明，塑性混凝土无侧限受应力－应变曲线上割线点的选取不同，其弹性模量的计算值不同.E27大于E26和E28的值，E27与二者比值的平均值分别为1.05和1.02；E37大于E38的值，二者比值的平均值为1.04，说明割线点P1选取过小或点P2选取过大都会造成塑性混凝土弹性模量计算值的减小.E37和E36较为接近，原因在于0.3倍峰值应力到0.7倍峰值应力上升段中，塑性混凝土基本呈线性变形，应力－应变曲线大致为直线［7］.

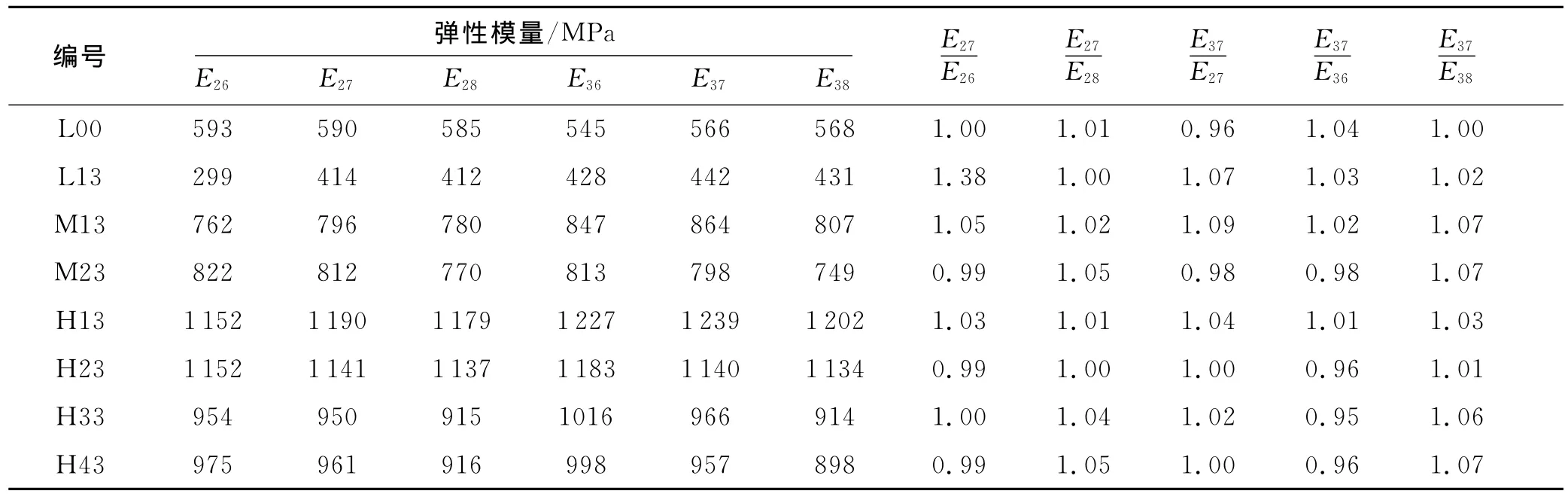
表2 塑性混凝土不同弹性模量计算方法的计算结果对比

各组塑性混凝土配合比的E37弹性模量值与其余几种方法计算的弹性模量值统计关系列于表3.统计表明，各配合比的E37与E36比值的离散程度与E37与E38比值的离散程度相同，同时E37与E36和E38的线性关系均较好.但从平均值看，E37与E36更为接近，E37与E36的数值近似程度和线性相关关系要好于与其他几种方法计算的弹性模量值的近似程度和相关关系.可以认为，塑性混凝土受压应力－应变曲线上升段中从0.3倍峰值应力到0.7倍峰值应力为较为稳定的阶段，采用E37和E36的方法计算其弹性模量数值相差不大.然而塑性混凝土强度较低，数据点的离散性较大，在满足线性关系的前提下，为减小误差应尽可能的扩大弹性模量的计算区间［6］，建议塑性混凝土弹性模量计算可取受压应力－应变曲线上0.3倍、0.7倍峰值强度对应点的割线斜率.

表3 计算弹性模量值之间关系参数

4 结 论

通过塑性混凝土弹性模量试验的归纳与研究，对其计算方法中P1和P2点的选取进行讨论，得出了以下结论:①塑性混凝土弹性模量取受压应力－应变曲线上0.3倍、0.6倍峰值强度对应点的割线斜率或0.3倍、0.7倍峰值强度对应点的割线斜率时，二者数值相差不大；②为减小误差，扩大计算区间，塑性混凝土弹性模量计算可取受压应力－应变曲线上0.3倍、0.7倍峰值强度对应点的割线斜率.

［1］王四巍.塑性混凝土弹性模量室内试验研究［J］.水文工程地质，2011，38（3）:73－75.

［2］高丹盈，付超云，赵利梅.加载速度对塑性混凝土强度的影响［J］.人民黄河，2009，31（6）:115－116.

［3］王清友，孙万功，熊 欢.塑性混凝土防渗墙［M］.北京:中国水利水电出版社，2008:78.

［4］李清富，张 鹏，张保雷.塑性混凝土弹性模量的实验研究［J］.水力发电，2005，31（3）:30－32.

［5］王四巍，于怀昌，高丹盈，等.塑性混凝土弹性模量室内试验研究［J］.水文地质工程地质，2011，38（3）:73－75.

［6］杨 林，杨 静，季洪奎.塑性混凝土弹性模量研究［J］.三峡大学学报:自然科学版，2012，34（5）:66－68.

［7］高丹盈，赵利梅，王四巍.塑性混凝土弹性模量的计算方法［J］.郑州大学学报:工学版，2009，30（4）:15－17.

［8］赵利梅.塑性混凝土基本力学及变形性能研究［D］.郑州:郑州大学，2009.

［9］中国水利水电第十四工程局有限公司.一种测定塑性混凝土弹性模量的试验方法:中国.201010249723.7［P］.2011－07－06.