基于环形阵列扭矩传感器的高精度扭矩测量系统设计*

喻洪麟，陈 薇，何安国

（1．重庆大学光电技术及系统教育部重点实验室，重庆 400044;2．重庆大学自动化学院，重庆 400044）

0 引言

扭矩测量是研究大型机械传动系统在各种载荷和工作环境下动态特性的关键方法，受到越来越多专家与工程技术人员的高度重视。目前，国内外采用在旋转轴表面粘贴应变片、涂敷磁致伸缩材料、放置压电晶体和弦振等［1，2］方式感受旋转轴的变形来测量扭矩，这些测量方法只是适用于一般的工程环境，当所处的环境异常恶劣（高温、振动、电磁干扰等）时，这些常规的扭矩的测量方法很难获得准确的数据［3］。因此，国内外众多专家学者都致力于新型的扭矩传感器及其测量系统的开发与研制。

环形空间阵列扭矩传感器是一种基于交流电磁感应技术的非接触式传感器［4］，其器件和电路元件均密封于机壳内，不受测量环境因素的影响，比较适于极端恶劣环境下扭矩动态测量，本文针对环形空间阵列传感测量系统测量精度不高与噪声干扰的问题，结合环形空间阵列传感器的工作原理与输出信号特点，设计了测量系统框架，并利用多重相关法来降低信号干扰和求解相位差，比较适用于环形空间阵列空间传感器，满足极端环境下机械传动轴扭矩的动态测量。

1 环形阵列器工作原理

传感器主要由环型空间阵列和磁电式检测器组成，如图1所示。

图1 环形阵列器原理结构图Fig 1 Structure of ring array sensor

环型空间阵列由1个非磁性不锈钢管构成，管内塞满紧密排列且特性完全相同的高精度磁性钢球，磁电式检测器固定在环形空间阵列外部且能屏蔽外部环境的电磁干扰，内部固定2组特殊线圈与部分处理电路。传感器随轴系转动时，检测器将相对于环形球阵列运动。当检测器内部的感应线圈1/2/3/4运动时间为t时，并设某一磁性小球的球心为O点，此时所对应的互感系数为

其中，ω0为轴的角速度，R为球心到转轴轴心的距离，D为磁性钢球的直径，k1为常量，与ω0和激励线圈的等效电阻与电感有关，A为互感系数产生的直流分量。

当施加的激励信号为U=U0sinωt，转轴不受扭力时，感应线圈输出电压为

其中，k2为常量，k=k1k2，从上式明显可以看出:感应线圈的输出电压是一个调幅信号，对其进行解调即可得环形阵列器旋转t时所产生的位移与角度。

2 环形阵列器的测量框架

针对环形阵列器的输出信号微弱且存在较大的干扰，系统采用三星公司生产的基于ARM920T内核的S3C2440AL芯片，其总线采用最新的AMBA架构，时钟频率高、处理速度快，能够完成比较复杂的数据处理运算［5，6］。S3C2440AL外设接口丰富，无需再额外添加外围扩展器件，功耗低、简单方便，特别适合用于对成本与功率要求比较高的应用，根据传递扭矩测量方法，设计出基于环形阵列器的扭矩测量系统如图2所示。两路具有相位差的调幅信号经过信号调理（包括放大、整形及滤波等）转换为适合A/D转换器采样的电压信号，经过多重相关器进一步转化和去噪，由A/D采样，再经微控制器控制经串口上传至上位机系统显示。

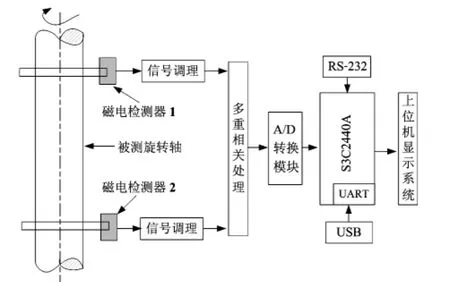
图2 测量系统结构图Fig 2 Structure diagram of measuring system

该测量系统中，当转轴受到扭矩的作用时，固定环形阵列器的2个横截面将会产生相对运动，即产生一个相应的扭转角φ，此时表现为感应线圈的感应电压的相位变化

考虑到扭转角不会很大，则可以由以上两调制信号之间的相位差φ得出旋转轴的扭转角，即

将上式带入传递法扭矩测量公式［7］，既可以通过转轴两端安装的环形阵列器输出电压信号的相位差又可得旋转轴所受到扭矩值。

2．1 信号调理模块设计

环形空间传感器主要是利用电磁感应原理将轴所受扭力矩的变化转换为能用数字表征的电信号的变化，信号微弱调幅的信号，必须经过放大、整形及相位求解后才能被转换成数字信号，最终显示在上位机显示屏中。模拟信号的处理是影响整个测量系统性能的重要因素之一，设计时要注意保证信号的质量，提高信噪比，尽量减少畸变;根据采集模块的A/D芯片设计比较合理的驱动电路。系统设计的调理电路运算和滤波主要采用低噪声、高精度芯片OPA2227，其还具有抗混叠的优越性能，如图3所示。图中S1为磁电检测器1端的模拟信号输入，REFI和REFO构成差分电路，经初步处理的信号以差分方式进入到A/D转换模块。

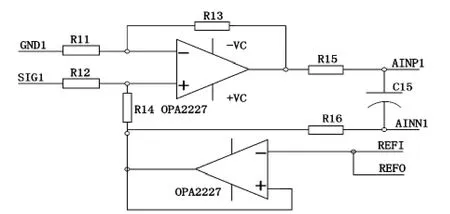
图3 信号调理电路Fig 3 Signal conditioning circuit

2．2 A/D转换模块与S3C2440AL接口设计

S3C2440AL自带8通道10位A/D转换器，其转换精度却难以满足本工业级测量系统的需要，系统选取TI公司24位高精度A/D转换器ADS1274，根据采集的速度和耗能要求设置其工作模式，无需寄存器编程，数据输出选择SPI串行接口，便于与控制器连接。ADS1274工作温度范围为－40～+125℃，抗振动，能在恶劣环境下正常工作。系统采用SPI接口协议和TDM动态位置分配数据格式，系统中控制器与A/D芯片的接口如图4所示。

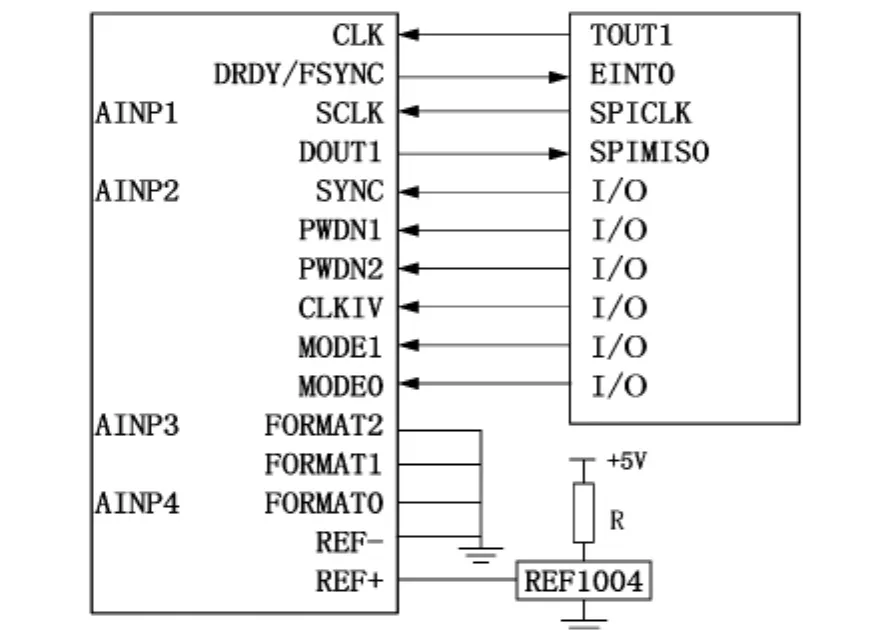
图4 控制器与ADS1074接口连接原理图Fig 4 Connection principle of controller and ADS1274 interface

系统采用 SPI协议，ADS1274工作时时钟最高为27 MHz，转换频率就高达105．469 kHz，通过设置控制器的PWM来设置 ADS1274采样频率，通过管脚 TOUT1为ADS1274提供时钟信号CLK，设置ADS1274的工作模式为高速模式，则采样频率fs=fpwm/256。由于控制器的管脚TOUT1最高频率为12．5 MHz，则最高采样频率也高达48．82 kHz。

3 多重相关法求相位差

经过放大整形后的信号仍然是调幅信号，必须对传感器的输出信号进行解调［7，8］，经过解调后的传感器感应线圈信号为

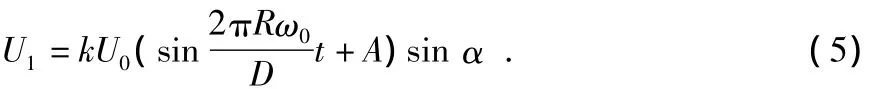
其中，α为常量，与感应线圈电压与激励线圈电压故有相差。

经过前期调理后的信号还会有环境噪声、A/D量化噪声、放大器噪声等，如果直接求取其相位差来计算扭矩值会存在较大的误差，会严重影响系统的测量精度，一般这些干扰信号在形式上与白噪声非常接近，与系统中的有用信号相关性非常小，利用多重自相关［9］可极大地提高信号的信噪比，多次互相关则可准确地提取被噪声严重干扰的相位差。测量框图如图5所示。

图5 多重相关法测量相位差框图Fig 5 Block diagram of phase difference measurement by multiple correlation

传感器的输出信号含有交流电磁感应产生的直流分量，滤除直流成分后的信号是含噪声的调制信号，两环形阵列器输出的含有噪声N（t）信号可以表示为

令K=kU0sin α，对U1取自相关运算得

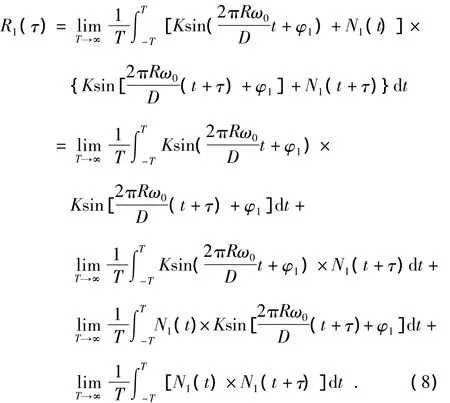
式（2）中的第一项是信号的自相关函数，第二，三项是信号与噪声以及噪声与信号的互相关函数，最后一项是噪声的自相关函数。理论上，环境噪声和采集电路噪声都是各自具有的相关性非常弱，也即当T趋向无穷大时，后三项基本趋于零，故经过一次自相关运算的信号可以表示为

从式（9）可以看出:信号经过一次自相关后相位信息丢失了，而信号的幅值与频率则可以根据解析关系计算出。但是实际上T不是趋向无穷大的，这就使得后三项不是完全为零的，故经过一次自相关后的信号可以表示为

其中，N'1（t）比原来的噪声N1（t）小很多，此时不但信号的信噪比大大提高了，也提高了信号相位差的测量精度，对两环形阵列器输出信号求互相关运算

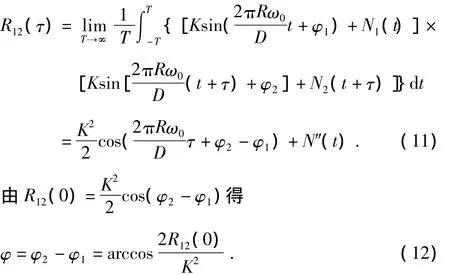
信号在取一次自相关运算后频率不变，相位变为零，噪声大幅度减少;信号在取一次互相关运算后频率不变，相位差的值保留下来，同时信号噪声也大幅度减少，干扰得到较好抑制。如再根据多重相关原理将自相关器与互相关器的各自输出信号看成新的信号，然后依次通过多个相同的自相关器与互相关器进行运算，就能够基本滤除干扰信号，极大地提高相位差测量的准确度，进而整个扭矩测量系统的测量精度也会有较大幅度的提高。

4 实验验证

根据图2所示的测量系统将2个内球直径均为12．7 mm环形阵列传感器安装到的传动轴上，间距为1 m，并施加幅值为5V、频率为1kHz的激励信号，搭建的实验平台如图6所示。

图6 传感器信号测试装置Fig 6 Testing device of sensor signal

测量系统中ADS1274在微控制器S3C2440AL的控制下进行数据的采集，采集的速率设置为20 kS/s。鉴于工程应用的要求，一般取两次到三次相关即可以满足。实验时，保持转轴转速不变，连续变化所加载在转轴上的标准扭矩值，并将采集到的相位差通过串口上传到PC机，再经过一系列的运算求出所加载的扭矩值，分别记录一次相关与二次相关所采集的相位差φ1，φ2以及其运算后的扭矩值N1，N2部分数据如表1所示。

为了更为直观地反映多次相关测量数据的准确性，将一次相关与多次相关所得到的相差与理论相差以散点形式描绘，如图7。

从图中数据可以看出:二次相关求得的相位差比一次相关更接近理论值，表中实测扭矩值也更接近扭矩标准值，精度也相应提高，也就是说无需对系统进行硬件软件的大规模改动就提高了系统相位差测量精度，即准确获取了传动轴所受扭矩。表1中数据还显示:在传动轴未加载扭矩时，两环形阵列器信号之间仍有相位差，这主要是由环形阵列器的安装位置之间有一定的距离引起的，可以归结为系统误差，通过系统误差修正和数据标定来解决，同时也说明，该扭矩测量系统具有较高的灵敏度，精度也满足系统要求。

表1 实验测量数据Tab 1 Experimental measurement data

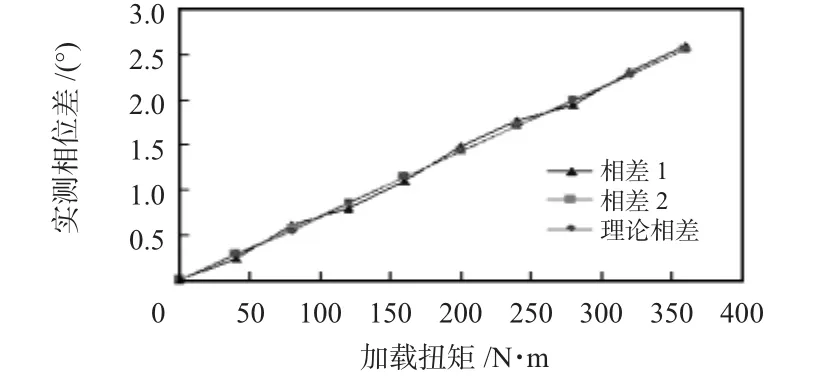
图7 相位差数据散点图Fig 7 Scatter diagram of phase difference data

5 结论

本文针对环形阵列扭矩传感器特殊结构与工作原理搭建一个以S3C2440AL为核心的非接触扭矩测量系统，重点研究了环形空间阵列器的输出信号特点，利用多重相关法对传感器双通道的信号进行处理，降低噪声干扰与提高相位差测量精度，进而提高整个扭矩测量系统的测量精度，同时实验数据也表明该测量系统是可行的，能实时动态地反映传动轴所受扭矩的变化。此外，该测量系统体积小、功耗低，在震动、高温条件下能够有效运行，比较适用于恶劣环境。

［1］ 柴继新，王恩峰，范小燕，等．几种常见的电阻应变式旋转扭矩传感器［J］．计测技术，2010，30（2）:34 －36．

［2］ Vega J，Ruiz M，Sanchez E，et al．Real-time lossless data compression techniques for long-pulse operation［J］．Fusion Engineering and Design，2007，82:1301 －130．

［3］ 胡 泽，肖宇恒，葛 亮，等．应变式井下工程参数测量传感器组桥与布片研究［J］．自动化仪表，2012，33（5）:77 －79．

［4］ 吴永烽，喻洪麟，何安国．环形球栅扭矩测量原理研究［J］．仪器仪表学报，2010，33（11）:2580 －2585．

［5］ 钟小勇，张小红．基于ARM的钢丝绳检测系统研究［J］．传感器与微系统，2011，30（3）:81 －83．

［6］ Qin Xu，Fan Panguo，Xu Zhuoju．A new design of high-speed multi-task real-time data acquisition system［J］．Computer Measurement＆ Control，2010，18（10）:2444 －2447．

［7］ Guo Dongmei．Quadrature demodulation technique for self-mixing interferometry displacement sensor［J］．Optics Communications，2011，284（24）:5766 －5769．

［8］ 孟 鑫，宫铭举，张爱玲，等．一种光源调频的相位生成载波的反正切解调方法［J］．天津理工大学学报，2012，28（3）:38－40．

［9］ He Xianlong，Zhao Lizhen．Analysis of shear wave velocity based on multiple cross-correlation functions［J］．Rock and Soil Mechanics，2010，31（8）:2541 －2545，2552．