基于EEMD能量熵和LSSVM的传感器故障诊断*

丁国君，王立德，申 萍，杨 鹏

（北京交通大学电气工程学院，北京 100044）

0 引言

传感器在动车组制动控制系统中负责对电压、电流、速度、压力和温度等信号的采集与调理，输入到制动控制单元进行演算和计算，输出制动控制力，并根据传感器信号的变化实时调整制动力的大小，所以，传感器发生故障将对动车组的制动性能产生重要影响。传感器的故障类型主要有偏差故障、冲击故障、噪声干扰故障、漂移故障、输出恒定值故障和周期性干扰故障6种类型［1］。当传感器发生故障时，传感器的输出信号表现为非线性非平稳信号，信号中包含丰富的时域和频域信息，因此，需要使用时域和频域相结合的故障特征提取方法才能很好地提取出传感器的故障信息。

基于信号处理的人工智能方法越来越多地被应用于传感器的故障特征提取和诊断中，目前应用最广泛的传感器故障特征提取方法和故障诊断方法分别是小波分析技术和人工神经网络［2～4］，但是，小波分析存在低频区间分析较粗糙、不会自适应等缺点，人工神经网络的选择和容易陷入局部极小点、过学习等问题都是其不容忽视的缺陷。

本文提出了利用集成经验模态分解（EEMD）方法对传感器输出信号进行若干内禀模态函数（IMFs）的分解，同时提取不同层次IMFs分量的能量熵作为故障特征向量，这样既解决了EMD的模态混叠和端点效应，也解决了小波分析方法在缓变信号的局限性，使传感器故障特征提取更加准确。同时利用最小二乘支持向量机（LSSVM）的小样本和风险最小化的特点，能够迅速地进行故障识别和分类，具有很高的识别精度和速度，对传感器故障进行诊断。

1 基本原理

1．1EEMD

EEMD方法基于信号的局部特征的时间尺度，克服了EMD方法的端点效应和模态混叠现象，分解出的各个IMFs突出了数据的局部特征，对其进行分析可以更有效地掌握原始数据的特征信息，每一个IMF都是自适应的，EEMD步骤如下［5，6］:

1）均匀添加白噪声序列（均值为0，标准差为常数）到目标数据序列上

其中，x（i）为原始信号，n（i）为添加的白噪声，α为添加白噪声系数，一般取0．1～0．4之间。

2）将加入了白噪声序列的数据用常规的EMD分解为多个IMFs，得到IMF分量cs（i）和余项rs（i）

3）重复迭代步骤（1）和步骤（2），但每次加入的是不同幅值的白噪声序列。

4）将分解得到的相应IMFs的均值作为最终的分解结果

当N越大，对应的白噪声的IMFs的和将趋于0，则EEMD的结果为

1．2 LSSVM 原理

SVM克服了神经网络网络结构确定困难、收敛于局部极小和不适合小样本等缺点，有效解决了小样本、高维数和非线性等学习问题。但在实际应用中，采用逼近算法和多类分类不如两类分类效果显著等不足，训练速度慢，造成SVM泛化能力的下降［7］。

LSSVM 是由 Suykens J A K 和Vandewalle J［8］提出的对SVM的一种改进算法，它用二次损失函数取代SVM中的不敏感损失函数，通过构造损失函数将原SVM中算法的二次寻优变为求解线性方程，降低了计算的复杂性，具有更好的抗噪能力和更快的运算速度。

分类问题的目标是求解决策函数y（x）=sgnf（x），其中，函数f（x）形式如下

其中，φ（．）为输入空间到特征空间的非线性映射，系数向量w和偏差项b为待求量。然后在该映射空间构造分类函数式（6）

其中，ai为拉格朗日乘子，K（x，xi）为满足Mercer条件的核函数，b为偏差量。

典型的核函数有多项式核函数、径向基（radial basis function，RBF）核函数和Sigmoid核函数等。本文采用性能较好的RBF核函数作为LSSVM核函数，其表达式为K（x，xi）=exp（－‖x－xi‖2/σ2），需要优化的参数有正规化参数γ和核函数参数σ2。

2 故障特征提取

由于EEMD的前几个IMFs分量就包含了原始信号中大部分的信息，而当传感器发生故障时，IMFs的能量熵发生变化，因此，可以从IMFs能量熵入手，通过提取IMFs的能量熵来提取传感器的故障特征信息，具体的分解步骤如下［9］:

1）对原始信号进行EEMD，选取包含故障主要信息的前n个IMFs分量。

2）求各个内禀模态函数的能量Ei

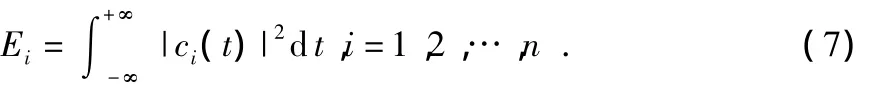
3）所有的IMFs能量熵组成特征向量T

4）为了更好地提取故障特征信息，对每一个IMFs能量熵作归一化处理

5）可得归一化处理后的故障特征向量

T'向量可作为LSSVM分类器输入的故障特征向量。

为了验证EEMD方法的有效性，对仿真的传感器的冲击故障分别利用不同故障特征提取方法提取故障特征，并对比分析。

图1是仿真的传感器冲击故障的输出电压信号，图2是EMD后的冲击故障的传感器输出信号波形，传感器冲击故障的输出信号经过经验模态分解后，共分解为8个IMF分量和残余项，由于冲击信号是突发的非线性非平稳信号，在EMD分解过程中出现了模态混叠现象，这影响对传感器冲击故障特征的准确提取。

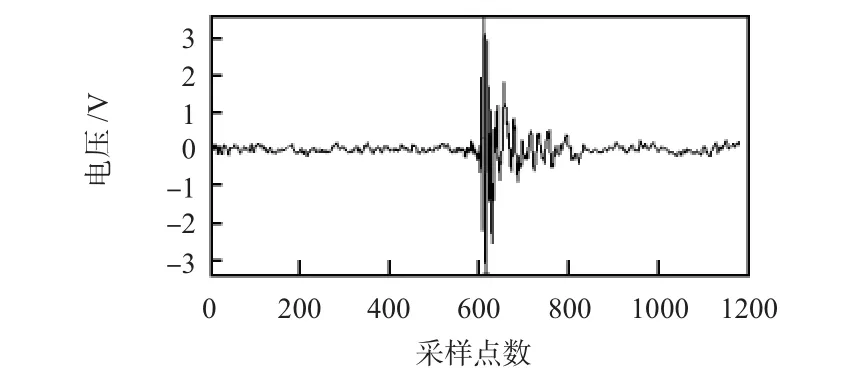
图1 冲击故障仿真信号Fig 1 Simulation signal of impact fault

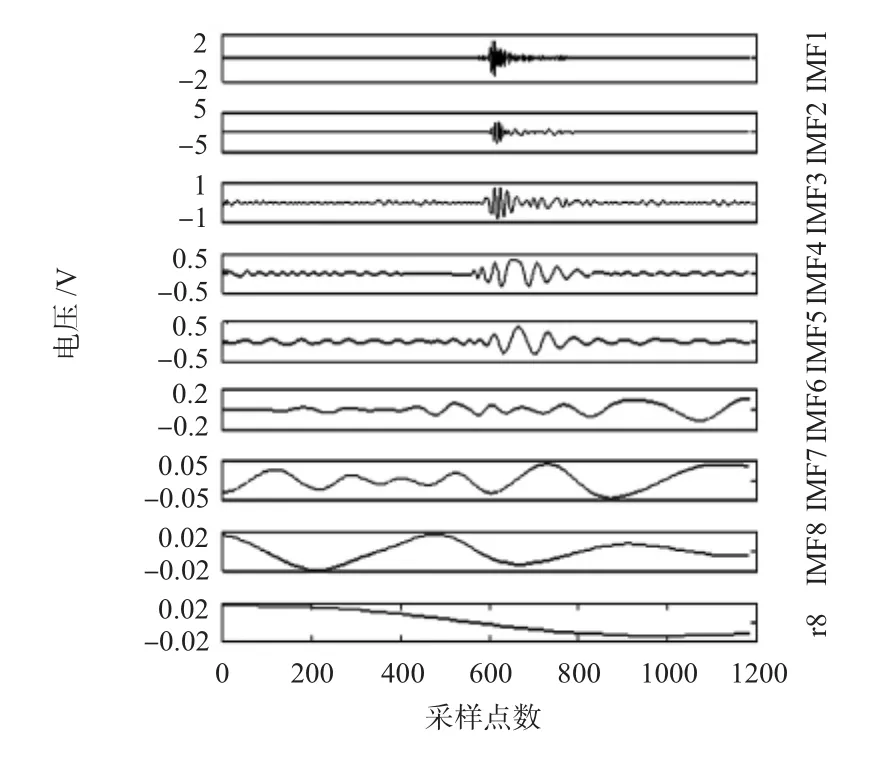
图2 冲击故障的EMD分解波形Fig 2 EMD decomposition waveform of impact fault

图3是传感器冲击故障信号经EEMD的波形图，冲击故障输出信号被分解为8个IMF分量和残余项，每个IMF分量均清晰地表征了冲击故障信号的详细特征信息，没有出现模态混叠现象。

图3 冲击故障信号EEMD分解波形Fig 3 EEMD decomposition waveform of impact fault signal

根据EEMD能量熵分解步骤（1）～（5），分别对不同故障模式下的传感器故障信号按照式（1）～（4）进行EEMD，并提取前8个IMF分量的能量熵，经过归一化处理后形成传感器故障特征向量，部分传感器故障特征向量数据样本如表1所示。

表1 基于EEMD能量熵故障特征提取方法的部分传感器故障样本Tab 1 Part of sensor fault sample based on EEMD energy entropy fault feature extraction method

3 LSSVM结构参数优化

LSSVM的正规化参数γ和核函数参数σ2的选取直接影响到LSSVM的分类和泛化能力。常见的参数优化算法有:试凑法、网格搜索法和三步搜索法等，前2种算法运算复杂用时长，未必能找到全局最优解;三步搜索法虽然运算时间短，但是主要依靠人工经验，不一定能寻找到最优参数。

粒子群优化（PSO）算法是一种基于迭代的启发式并行搜索进化算法，是由美国学者Kennedy J和Eberhart R C［10］受鸟群觅食行为的启发而提出的群智能优化算法。

PSO算法是一种基于迭代的启发式并行搜索进化算法，其速度和位置更新的方程如式（11）和式（12）所示

其中，vid和xid分别为粒子i在d维中的速度和位置;pid为粒子i在d维中的最优值;pgd为所有粒子在d维中的最优值;w为惯性权重;c1和c2为学习因子;r1和r2为 之间的随机数。

4 实际测试分析

为了比较不同故障特征提取方法的分类性能，选取动车组制动系统的AS压力传感器作为研究对象，对7种传感器状态下各100组数据，然后随机选取50组样本进行训练，利用余下的各50组进行测试。BP神经网络采用8—16—7结构，小波包采用三层小波包分解，并提取小波包能量熵［2］。LSSVM采用“1—V—1”多类分类器，共设计21个两类分类器。运用PSO算法对LSSVM模型的正规化参数和核函数参数进行优化，得到最佳的正规化参数γ=115．26，核函数参数σ=0．54。根据不同的故障特征提取方法和故障诊断方法得到的诊断结果如表2所示。

表2 故障诊断结果Tab 2 Results of fault diagnosis

从传感器故障分类识别结果可以看出:提出的基于EEMD能量熵的故障特征提取方法的故障分类结果正确率最高，对传感器的冲击故障、周期干扰故障和噪声干扰故障的正确分类率达到100%，远高于基于小波包故障特征提取方法和BP神经网络分类方法的故障正确分类率，验证了提出的故障特征方法和故障诊断方法的有效性。

5 结论

针对动车组制动系统的传感器故障，提出了基于EEMD能量熵和改进LSSVM的故障诊断新方法。基于EEMD能量熵的故障特征提取方法可准确可靠地提取传感器的故障特征信息，采用PSO算法优化LSSVM的结构参数可以获得更优的结构参数组合，能够显著提高LSSVM的分类能力和泛化能力。实验结果表明:提出的诊断模型既有较高的故障正确分类率，也有良好的泛化能力。

［1］ 冯志刚，王 祁，信太克规．基于EMD和SVM的传感器故障诊断方法［J］．哈尔滨工业大学报，2009，41（5）:59 －63．

［2］ 冯志刚，王 祁，徐 涛，等．基于小波包和支持向量机的传感器故障诊断方法［J］．南京理工大学学报:自然科学版，2008，32（5）:609－615．

［3］ 李欢欢，司风琪，徐治皋．一种基于鲁棒自联想神经网络的传感器故障诊断方法［J］．中国电机工程学报，2012，32（14）:116－121．

［4］ 陈楚瑶，朱大奇．神经网络主元分析的传感器故障诊断方法［J］．系统工程与电子技术，2010，32（7）:1549 －1553．

［5］ Lei Yaguo，Lin Jing，He Zhengjia，et al．A review on ensemble empirical mode decomposition in fault diagnosis of rotating machinery［J］．Mechanical Systems and Signal Processing，2013，35（1－2）:108－126．

［6］ Wu Zhaohua，Huang Norden E．Ensemble empirical mode decomposition:A noise-assisted data analysis method［J］．Advances in Adaptive Data Analysis，2009，1（1）:1 －41．

［7］ 蒋少华，桂卫华，杨春华，等．基于RS与LSSVM多分类法的故障诊断方法及其应用［J］．中南大学学报:自然科学版，2009，40（2）:447－451．

［8］ Suykens J A K，Vandewalle J．Least squares support vector machine classifiers［J］．Neural Processing Letters，1999，9（3）:293－300．

［9］ 张 超，陈建军，郭 迅．基于EEMD能量熵和支持向量机的齿轮故障诊断方法［J］．中南大学学报:自然科学版，2012，43（3）:932－939．

［10］ Kennedy J，Eberhart R C．Particle swarm optimization［C］∥Proceedings of IEEE International Conference on Neural Networks，NJ，1995:1942 －1948．