均匀圆阵下单个近场源信号四维参数估计快速算法

吴云韬，张彦斌，曹 辉，汪 海

（1.武汉工程大学计算机科学与工程学院，湖北 武汉 430074；2.武汉工程大学智能机器人湖北省重点实验室，湖北 武汉 430074）

0 引 言

利用空间位置分散的阵元组成的阵列来进行空间信号源定位在雷达、声纳和无线通信等方面有着重要的应用.而用均匀圆阵（Uniform Circle Array，以下简称：UCA）估计信号源位置相对于其它阵列结构有着360°的全方位角覆盖范围、几乎不变的方向图和额外的俯仰角信息等优点［1－2］.近年来，文献［1－4］研究了基于圆阵的近场源无源定位问题.文献［2］中首先利用三维多重信号分类算法（3－Dimensions Multiple Signal Classification Method，以下简称：3－D MUSIC）来联合估计出近场源的方位角、俯仰角和距离［2］，但基于 MUSIC的方法由于需要3－D搜索计算因而计算复杂度高而难以工程实时实现.通过在UCA阵的中心增加一个阵元，Bea［3］等最近提出了一种计算量比较小的基于最小二乘（Least Square，LS）的近场源定位算法，但是这种方法只适用于非圆信号源.笔者提出了一种基于最小二乘的快速信源定位算法，该算法首先给出方位角、俯仰角和频率的估计，然后再估计出距离参数.和文献［3］不同的是，该方法无需利用UCA中心的参考阵元，且信号源无需非圆特性假设.该算法的核心思想是利用UCA的中心对称结构构造出两个相关序列，且该相关序列的相位上包含信号的位置信息，然后利用构造的相关序列的相位信息估计出信号源的4－D参数.值得注意的是所提算法可以认为是远场定位方法的一个推广.仿真结果表明提出的算法和单个信号源的4－D MUSIC算法在性能上相当，但在计算复杂度上所提算法因不需要三维搜索和特征分解而具有显著优势.

1 提出的方法

假定中心对称均匀圆阵的半径为R，且放置M（2的倍数）个阵元，所有的阵元分布在xy平面上，且UCA的中心为相位参考点.假设窄带近场信号源在球面坐标系统上的位置参数为（θ，φ，r）：θ∈［0，2π）是信号的方位角，表示从x轴的正方向按逆时针方向所旋转的角度；φ∈［0，π／2）是信号的俯仰角，表示从z轴的正方向按从上往下所旋转的角度；距离r是信号离UCA中心的距离，设w0是信号载波的频率，则第k个阵元上的接收数据可以写成［2］：

式（1）中：s（n）为零均值的复窄带信号，其功率为E［｜s（n）｜2］＝，E［·］为期望运算符；噪声｛wk（n）｝是各态历经、零均值、空域和时域上的复白高斯过程，且和信号源相互独立；N为快拍数；λ是信号的波长；rk（θ，φ，r）是信号源和第k个阵元间的距离，它可以写成如下的形式：

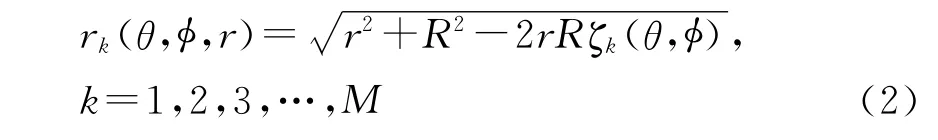
这里，

γk＝2π（k－1）／M 为第k个阵元的方位角.我们的任务是在获得｛xk（n）｝后估计θ，φ，r，w0.

当r足够大时，根据泰勒展开，式（2）可以近似为：

把式（4）带入到式（1）中，有

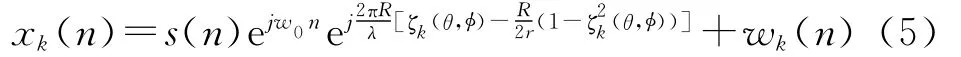
在阵列配置的中心对称性和阵元数为偶数的假设下，可以得到γM／2＋k＝γk＋π，并由此可以得到：

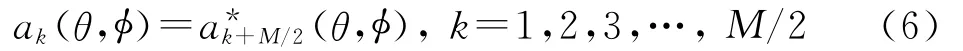
式（6）中：ak（θ，φ）为第k个阵元对信号源的复响应.（·）＊为复共轭算子.同时有关系式γM／4＋k＝γk＋π／2，由此可以得到：

根据式（6）和式（7），利用｛xk（n）｝构造两个相关序列且：

当N和信噪比都足够大时，且当各态历经条件成立时，xk（n）≈xk（n＋1），p（k）可以近似表示为［1］，

同样的，式（9）可以如下近似：

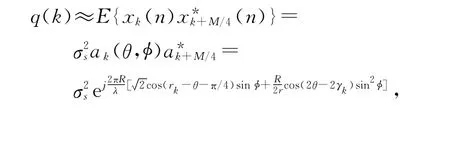
1.1 信号源角度和载波频率的估计

首先从式（10）中估计出θ、φ和w0，然后从式（11）中估计出r.令wk为p（k）的相角，从式（10）中可以得到

式（12）中mk为整数.假设式（12）中的相位模糊问题已经通过选择适当的mk得到解决［5－6］，这样就可以得到唯一的角度估计.不失一般性，假设mk＝0，于是式（12）可以写成

这里，（·）T为转置算子.于是b的最小二乘估计，写成，为

对θ，φ，w0的估计，写成，可以由给出：

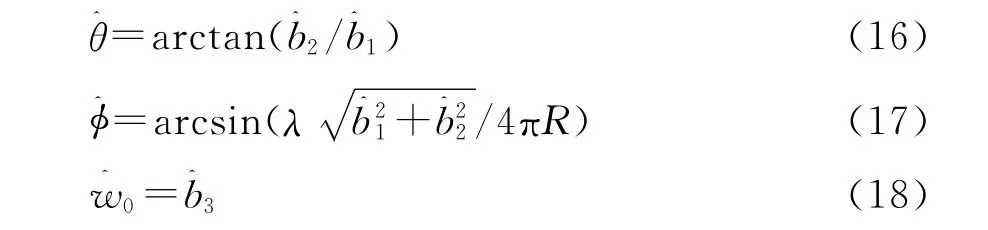
需要指出的是，上述估计步骤和文献［4，6－7］是一样的.

1.2 信号源距离的估计

利用前面估计的角度结果，笔者将给出距离的估计，设uk为qk的相位，可以从式（11）中得到如下关系：

将式（19）表示成矩阵形式有，

这里，

2 仿真结果

笔者将所提算法和3－D MUSIC［2］的性能在MATLAB环境下进行比较，入射信号为单个窄带近场信号，噪声为加性高斯白噪声.设定仿真参数M＝8，R＝λ＝1，信号参数为（θ，φ，r，w0）＝（70，10，1.5R，0.2），快拍数 N＝200.用均方差来评价算法的估计性能，性能结果为300次独立运行的均值.图1～图4给出了所提算法proposed和传统的基于MUSIC方法的参数估计性能比较，图中均方误差越小越好.由图1～图4可以看出，两种方法的估计性能大致相当，但在计算复杂度方面，比较300次独立运算的总时间即单个信噪比（Signal to Noise Ratio，以下简称：SNR），所提算法只要0.2246s，而3－D MUSIC方法却要349.8254s，表明本文算法具有显著优势.

图1 θ的均方误差随着SNR的变化曲线Fig.1 Mean square error ofθversus SNR

3 结 语

本文针对UCA阵列结构，提出了一种对单个近场源信号进行定位的快速算法，并给出了信号的方位角、俯仰角、距离和载波频率参数的闭式解.仿真结果表明，所提算法在性能上和3－D MUSIC相近，但具有更低的计算复杂度而利于工程实时应用.该方法只能处理单个近场信号源，而无法解决存在多个信号源情况下的定位问题，推广到多个信号源是笔者需要进一步探讨的问题.

图2 φ的均方误差随着SNR的变化曲线Fig.2 Mean square error ofφversus SNR

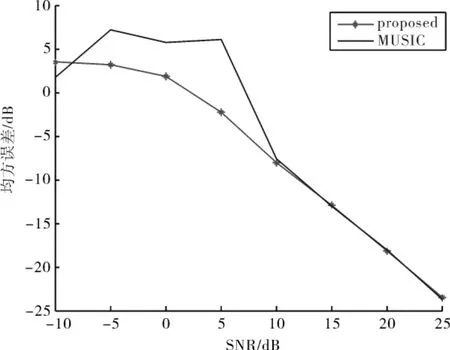
图3 r的均方误差随着SNR的变化曲线Fig.3 Mean square error of r versus SNR

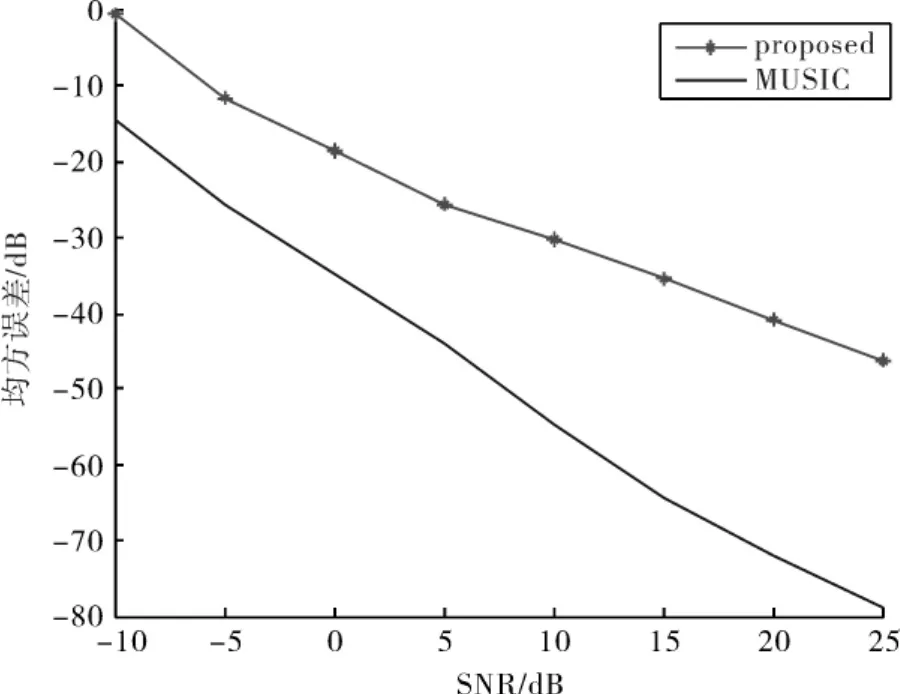
图4 w0的均方误差随着SNR的变化曲线Fig.4 Mean square error of w0versus SNR

［1］Wu Y T，So H C.Simple and Accurate Two－Dimensional Angle Estimation for a Single Source with Uniform Circular Array［J］.IEEE Antennas and Wireless Propagation Letters，2008，7：78－80.

［2］Lee J H，Park D H，Park G T ，et al.Algebraic path－following algorithm for localizing 3－D near－field sources in uniform circular array［J］.Electronics Letters，2003，39（17）：1283－1285.

［3］Bae E H ，Lee K K.Closed－form 3－D localization for single source in uniform circular array with a center sensor［J］.IEICE Transactions on Communications，2009，E92／B（3）：1053－1056.

［4］Wu Y T，W H，Huang L T，et al.Fast Algorithm for Three－Dimensional Single Near－Field Source Localization with Uniform Circular Array［C］／／2011 IEEE CIE International Conference on Radar Processing，Chengdu， China. October 24－27.Piscataway，NJ，United States：Institute of Electrical and Electronics Engineers Inc，2011，1：350－352.

［5］Zoltowski M D，Mathews C P.Real－time frequency and 2－D angle estimation with sub－Nyquist spatioemporal sampling［J］.IEEE Transactions on Signal Processing，1994，42（10）：2781－2794.

［6］Sundaram K R，Mallik R K，Murthy U M S.Modulo conversion method for estimating the direction of arrival［J］.IEEE Transactions on Aerospace and Electronic Systems，2000，36（4）：1391－1396.

［7］汪海.高分辨率的DOA估计算法研究及其系统实现［D］.武汉：武汉工程大学，2012.