人工神经网络在建筑材料价格预测中的应用

欧阳红祥，李 欣，张信娟

（1.河海大学 商学院，江苏 南京 210098；2.金桥房地产开发有限公司，江苏 常州 213000）

建筑工程中材料费的高低对工程造价有时起决定性的作用［1］。面对建筑市场激烈竞争的形势，投标人做好工程编标前的材料价格调查与预测是合理报价并确保中标的重要前提，也是确保企业盈利的关键一环。工程项目的施工周期一般较长，少则几个月，多则几年甚至十几年。在漫长的施工过程中，材料价格肯定会发生变化。在发包人与承包人签订的合同中，对材料价格上涨的处理主要有两种方式，一是材料价格完全不调整；二是对材料价格有限度地调整［2－3］。所谓材料价格不调整，顾名思义，是指在整个施工期间所有材料都不因市场价格上涨而作出调整，故承包商承担了材料价格上涨的风险。材料价格有限度地调整是指在工程施工期间，当材料价格波动达到一定幅度时，如上涨部分超过报价的10%或15%，对超过的部分进行调整。因此，限额内的材料涨价风险由承包商承担，而限额以外的涨价风险由业主承担，这种调价方式充分体现了风险分担的原则，因而在项目上被普遍采用。不管哪种方式，承包商都要承担一定的材料涨价风险，如果承包商在投标时，能充分了解市场行情，并能准确预测出未来的价格走势，无疑对提高中标的可能性以及中标后的获利能力有较大的帮助［4－5］。通过检索《中国期刊全文数据库》发现，关于神经网络在建筑材料价格预测中的应用研究成果较少。大多数文献侧重于以建筑结构参数作为主要特征指标，如基础类型、基底标高、工程类别、层数、层高和建筑面积等，选取一定的样本，训练BP神经网络，将主要特征指标值映射到造价指标，从而可实现工程造价的快速预测［6－8］；其不足之处在于特征指标的选取不统一，且特征指标的定量化随意性较大。笔者另辟蹊径，着重研究未来建筑材料的涨跌对当前投标报价的影响，辅助决策者进行正确决策。之所以选择BP神经网络预测建筑材料价格走势，是因为BP神经网络具有自学习、自组织与自适应性特征以及较强的非线性映射和泛化能力，特别适合解决市场预测问题。

1 BP神经网络模型

1.1 BP神经网络结构

采用BP算法的多层感知器，简称BP神经网络，是迄今为止应用最广泛的神经网络之一，尤其以3层感知器应用最为普遍。3层BP神经网络的结构如图1所示。

图1 3层BP神经网络结构

在上述3层感知器中，输入层输入向量为X=（x1，x2，…，xi，…，xN）T，隐含层输出向量为Y=（y1，y2，…，yj，…，yM）T，输出层输出向量为O=（o1，o2，…，ok，…，oL）T。输入层到隐含层的权值矩阵用 V 表示，V=（v1，v2，…，vj，…，vM）T，其中vj为输入层到隐含层中第j个神经元的权向量；隐含层到输出层的权值矩阵用W表示，W=（w1，w2，…，wk，…，wL），其中 wk为隐含层到输出层中第k个神经元的权向量；输出层期望输出向量用 D=（d1，d2，…，dk，…，dL）T来表示［9－10］。

BP神经网络的功能特性由输入层到隐含层，以及隐含层到输出层的权值决定，即由权值矩阵V和W决定。BP神经网络能够通过对样本的学习训练，不断改变神经网络的连接权值，以使神经网络的实际输出O不断地接近期望输出D（两者之间的差值称为网络输出误差E）［11］。权值不断调整的过程，也就是神经网络的学习训练过程，该过程一直进行到网络输出误差减少到可接受的程度或进行到预先设定的学习次数为止。

1.2 网络各层信号的数学关系

对于输出层，有:

式中:wjk为隐含层的神经元j到输出层的神经元k的连接权值。对于隐含层，有:

式中:vij为输入层的神经元i到隐含层的神经元j的连接权值。

以上两式中，变换函数f（·）均为单极性Sigmoid函数，即f（x）=，f（x）具有连续可导的特点，且有f'（x）=f（x）·［1－f（x）］。单极性Sigmoid函数图形如图2所示。有时也采用双极性Sigmoid函数，即 f（x）=。双极性 Sigmoid函数图形如图3所示。

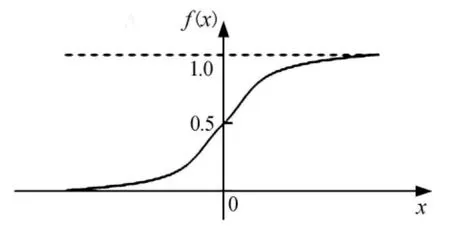
图2 单极性S型变换函数

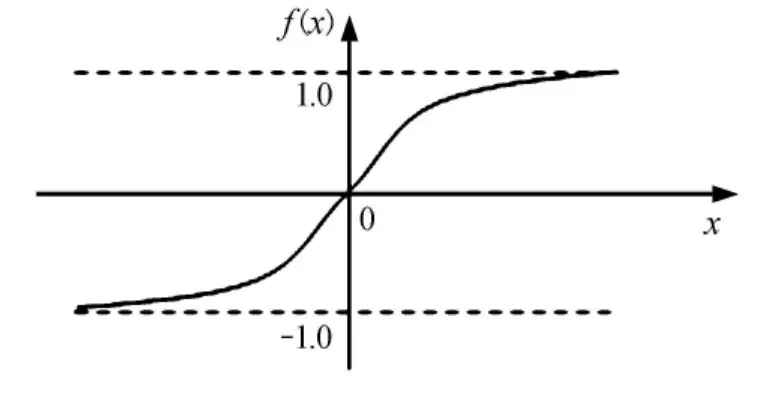
图3 双极性S型变换函数

1.3 网络输出误差与权值调整

当神经网络实际输出与期望输出不等时，意味着存在网络输出误差E，定义如下:

将式（3）逐步展开至输入层，可得:

由式（4）可见，网络输出误差E是各层权值wjk和vij的函数，因此调整权值可改变网络输出误差E的大小。显然，调整权值的原则是使误差不断地减小。3层BP神经网络权值调整计算公式如下:

1.4 神经网络价格预测流程

用BP神经网络预测建筑材料价格，首先应收集历史价格信息，然后设计BP神经网络参数值，用历史价格信息样本不断训练初始神经网络，直至训练精度达到规定要求，最后将测试价格数据输入到已经成熟的BP神经网络中，经过计算得到预测值。其流程如图4所示。

图4 神经网络价格预测流程

2 主要建材价格预测

建筑材料作为工程实体的一部分，在整个建筑工程造价中所占比例较大，有的甚至高达60%～70%，建筑材料价格的上涨必定引起工程成本的增加。因此，投标人在投标报价时应对未来建材价格走势有一个清醒的认识。在一般的建设项目中，主要建筑材料包括钢筋、水泥、砂石和混凝土等，笔者以螺纹钢（Ф12～Ф25）为例，详细介绍如何利用BP神经网络模型进行价格预测。假如工程造价部门颁布的某地区2011年螺纹钢（Ф12～Ф25）价格信息如表1所示。

表1 某地区2011年螺纹钢（Ф12～Ф25）市场价格

表1中的各月价格可用向量X=（x1，x2，…，x10）表示，对向量X按式（7）作归一化处理，得向量 Y={yi}=（0.000，0.375，0.417，0.708，0.792，0.708，0.625，0.583，0.792，1.000）。其关系为:

2.1 数据规范处理

钢材价格预测采用滚动预测方式，即用前4个月的市场价格来预测第5个月的价格。如用1、2、3、4月的市场价格预测 5月的市场价格，用2、3、4、5月的市场价格预测 6月的市场价格，依此类推，最后用6、7、8、9月的市场价格预测10月的市场价格。假如每组数据用矩阵的一列来表示，就得到输入矩阵P为:

将归一化处理后的 5、6、7、8、9、10 月的数据作为期望输出，即 T=（0.792，0.708，0.625，0.583，0.792，1.000）。期望输出和实际输出的差值就是输出误差E。

2.2 神经网络参数

采用3层BP神经网络结构。①输入层为4个神经元，代表4个月的价格。②隐含层则根据输入层和输出层神经元个数，参照经验公式，并经反复测试，确定选用8个神经元。隐含层的激活函数采用双极性Sigmoid函数。③输出层为1个神经元，用来输出预测价格。输出层的激活函数也采用双极性Sigmoid函数。④训练函数采用梯度下降函数traingd（）。⑤学习精度设为ε=0.005。

2.3 训练测试结果

采用Matlab软件提供的newff（）、tansig（）等函数，编制计算程序，经过3779次的学习，学习精度达到0.004995，满足预设的精度要求，其学习结果如表2所示，训练误差曲线如图5所示。其中，相对误差=（训练值－期望值）/期望值。

从表2可知，除8月份输出值与期望值数据出现较大误差外，其余学习样本的相对误差较小，平均误差为－2.49%，因而3层BP神经网络的学习结果应属理想。

表2 神经网络学习结果

图5 训练误差曲线

2.4 未来价格预测

根据训练成熟的BP神经网络，对未来6个月的钢材价格进行预测。例如以7、8、9、10月数据预测11月数据，然后以8、9、10、11月数据预测12月数据，依此类推，可预测出未来6个月甚至更多月份的数据。预测结果如表3和图6所示。

表3 神经网络预测结果

图6 神经网络价格预测

2.5 数据分析及对策

假如投标文件提交截止日期为10月31日，合同类型为单价合同，并且合同规定只有价格变动达到10%才允许调价。根据表1数据，10月份螺纹钢价格为4950元/t；表3数据显示，未来6个月螺纹钢的平均价格为4890元/t，材料价格降幅只有1.2%。因此，承包商不用担心合同价格的调整问题。考虑到未来6个月螺纹钢价格呈现下跌趋势，承包商可在正常报价的情况下，适当降低自身的报价，以提高中标的可能性。施工过程中，若材料实际价格走势与预测结果基本一样，承包商是没有任何损失的。

3 结论

在建筑企业投标活动中，能否快速而可靠地计算工程报价直接影响着中标的可能性。建筑材料作为工程实体的一部分，在整个建筑工程造价中所占比例较大，建筑材料价格的上涨必定引起工程成本的增加。因此，如何正确预测材料价格走势是一个热点难点问题。神经网络与其他预测方法相比，具有适应性强、容错能力好、非线性映射能力强等突出优点，可以有效地处理多因素非线性问题。笔者提出借助BP人工神经网络，用历史价格信息作为样本，预测未来价格走势的模型，可为承包商正确报价提供帮助。案例表明，该方法是可行且有效的。

［1］张登文，蒋红妍，张子圆.基于BP神经网络的建筑工程造价快速预测［J］.水利与建筑工程学报，2010（6）:61－62.

［2］胡洋，陈俊，蔡益民.基于遗传神经网络的报价决策模型研究［J］.水利经济，2008（7）:52－55.

［3］王运琢.基于BP神经网络的高速公路工程造价估算模型研究［J］.石家庄铁道大学学报:自然科学版，2011（6）:61－64.

［4］李晓娟.基于神经网络的工程造价估算模型研究［J］.甘肃联合大学学报:自然科学版，2011（7）:47－50.

［5］王新征，邢利英.基于BP神经网络的显著性工程造价估算方法［J］.人民黄河，2011（5）:115－117.

［6］彭军龙，张起森.基于神经网络的公路工程造价快速估算分析［J］.华东交通大学学报，2005（10）:41－44.

［7］辛立民，杨芸.基于神经网络的建筑工程投标报价预测［J］.安徽工程科技学院学报，2008（12）:44－47.

［8］贺玺.基于人工神经网络的投标报价确定［J］.山西建筑，2007（3）:245－246.

［9］韩力群.人工神经网络教程［M］.北京:北京邮电大学出版社，2006:12－132.

［10］张良均，曹晶，蒋世忠.神经网络实用教程［M］.北京:机械工业出版社，2008:22－76.

［11］王慧平.基于模糊神经网络的第三方物流项目风险预测［J］.武汉理工大学学报:信息与管理工程版，2010，32（5）:857 －860.