供应链联盟中合作伙伴之间的博弈分析

宗 涵

（西南交通大学 交通运输与物流学院，成都610031）

一、导论

新型的企业组织形式——供应链联盟正在逐步取代企业集团和战略联盟的位置，被视为未来企业组织形式发展演变的主流趋向。而要使这一组织形式健康发展，关键是要处理好联盟间的合作关系。供应链联盟之间的成员是否合作，本质上是企业双方的博弈问题。企业双方进行博弈，确定出能让自己收益最大的策略，从而决定是否进行合作。博弈论作为一种分析方法，不断被学者研究或运用。张维迎在《博弈论与信息经济学》中概括了博弈论的一些分析方法［1］；骆温平将博弈论引用到物流外包联盟中，分析了企业与第三方物流公司的合作关系［2］；李莹将博弈论应用到制造行业中，对比分析供应商之间的竞争条件［3］；曹倩文等运用博弈支付矩阵，构建了企业选择合作伙伴的关系模型，但只涉及一次合作的情况［4］；汤鹏等研究了不同供应链关系下的企业博弈问题及供应链契约选择问题［5］；Molander P和 Boerlijst M C等考虑了囚徒困境中以牙还牙策略对合作双方的影响［6－7］；Johnston D A等分析了合作双方的信任程度对供应链绩效的影响［8］。同样本文将博弈理论引入供应链合作伙伴关系研究中，将寻找联盟博弈看作一次性博弈，即考虑企业双方是否决定形成联盟，是否进行合作，而将维持供应链联盟看作是重复博弈，即长期动态博弈。先从一次博弈分析出发，建立合作伙伴关系博弈模型；再在此基础上进一步分析有限次数和无限次数博弈，即企业在供应链联盟中参与企业合作过程中的博弈，从中发现一些能促进供应链联盟中企业之间合作的基本规则和对策。

二、一次博弈分析

作为理性人（文章的所有内容都在参与者为理性人的基础上进行考虑），对合作与不合作策略的选择，必然是基于成本和收益比较考虑得到的。首先考虑到最为简单的情况——一次博弈，即供应链合作企业初次进行博弈，并且双方没有准备建立长期合作关系的情况。为了便于分析，假设有两个企业（甲方与乙方）参与博弈，且双方具有相同的收益结构和合作信息。用效用矩阵来表示双方博弈组合，如表1所示。这里的合作双方可以是第三方物流企业与供应链核心成员、供应商与制造商、供应商与供应商、制造商与制造商、供应商与销售商等。

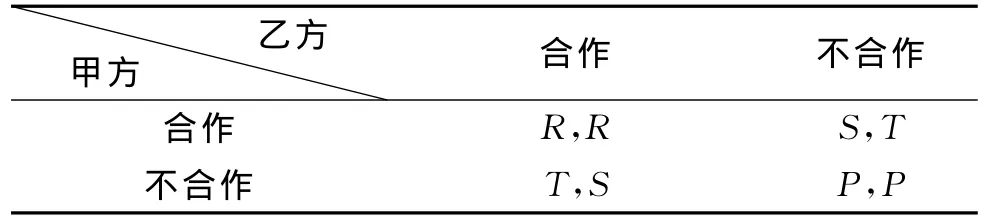
表1 合作双方（甲方与乙方）之间效用矩阵

如表1所示，甲方、乙方分别代表合作双方；R代表双方合作时每个企业的收益，R＞0；S表示对方不合作时的企业收益，R≠S；T表示背叛对方时自己获得的收益，T＞0；P表示双方企业都各自背叛对方时的收益，R＞P且T≠P。在一次博弈中，参数不同，该博弈模型均衡的结果将不同，其结果和文献［4］研究的结果一致。

当R＞T，S＞P时，双方都会选择合作策略是唯一的纳什均衡；

当R＜T，S＜P时，双方不合作是唯一的纳什均衡；

当R＞T，S＜P时，（合作，合作）和（不合作，不合作）是纳什均衡；

当R＜T，S＞P时，（合作，不合作）和（不合作，合作）是纳什均衡。

由此可得，当仅仅进行一次博弈时，甲乙两方将合作看为“一锤子买卖”，每个人都更着眼于短期利益，只考虑到一次性的收益。此时当对不合作方、不诚信方的处罚力度很小时，双方合作的概率将会很低。这种情形我们常见于旅游区或火车站餐馆和顾客之间的博弈，商家往往会考虑到顾客只会来一次，所以将顾客骗入商铺后，提供与先前承诺差距甚远的服务，以此来获得高额的欺骗效益。

在现实情况中，合作双方的收益情况满足时的博弈T＞R＞P＞S是最常见的，而此时博弈就如我们常见到的囚徒博弈。在只进行一次博弈情况下，策略组合（合作，合作）是不稳定的，如果一方认为另一方会合作的话，则它选择不合作的可能性很大。

三、重复博弈分析

要想使整个供应链具有较强的竞争力，供应链企业与企业之间的关系应是长期的、稳定的合作伙伴关系。如果交易一方为了一次性利润最大化而过多地损害交易另一方的利益，甚至多次损害对方的利益，这是得不偿失的事。因此在一个高效、稳定的供应链中，合作伙伴之间存在着重复博弈，任何博弈方博弈策略的选择依据都是得益的多少。此时的重复博弈常常不只是构成它们一次性博弈的简单重复，博弈结果也会出现更多可能性。为了便于分析，我们仍然考虑只有两个企业（甲方与乙方）参与博弈，且双方具有相同的收益结构和合作信息，并将这种重复博弈分为两种情况考虑——有限次数博弈和无限次数博弈。

（一）有限次数博弈

当交易双方在知道博弈将进行多少次后结束时，交易双方就进入了有限次博弈，此时交易双方在进行当期决策时，必然要考虑到以后的情况。以最常见的T＞R＞P＞S时的博弈进行分析。假设总共有X次交易，运用逆向归纳法，在最后一次X次合作时，博弈双方都会将博弈最后一阶段看为一次性博弈，因为双方都没有一个将来的奖励，双方都会选择不合作的策略，则双方收益都为P。在X－1次博弈当中，我们将X次的博弈收益加到前一次博弈结果中得到表2。

此时因为T＋P＞R＋P＞P＋P＞S＋P，与最后一次博弈结果相同，（不合作，不合作）仍然是唯一的纳什均衡，双方仍然会选择不合作。以此类推，在第X－2次、X－3次直到第一次博弈双方都会选择不合作作为自己的最优策略，从而自始至终都会背叛。

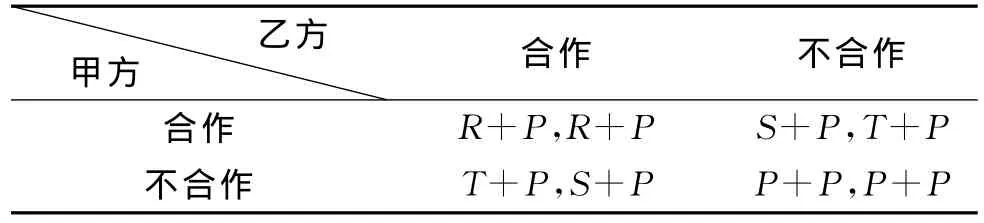
表2 合作双方（甲方与乙方）之间X－1次合作时效用矩阵

（二）无限多次博弈

当两家企业都不知道博弈要进行多少回合，如两家企业结成了长期的战略合作伙伴关系，企业间的交易可近似看成是无限次交易的过程，则买卖双方的博弈就是无限次重复博弈。如果参与人有足够的耐心，则博弈双方都合作将是一个子博弈完美纳什均衡结果，从而双方都会选择（合作，合作），而摒弃（不合作，不合作）。假设以一年为一个博弈阶段，将λ定为重复互动、持续下去的概率。现就常见的博弈战略（触发战略：一个参与者的不合作战略将会触发另一个参与者在下一轮的制度）及其收益情况进行分析。

一是豁免触发战略，其中包括“针锋相对（一报还一报）”“一报还两报”“慷慨的一报还一报”（如果对方的错误被控制在某个概率范围内，则本方保持合作策略）等策略。与Molander P［6］研究相似，我们以简单常见的“针锋相对”为例，即当一方一旦发现对方采用了不合作策略，则在下一阶段就采取不合作策略；当对方重新采取合作策略后，该博弈方随后也采取合作策略应对。此时当双方都合作时各方的收益设为U1；当对方一直采用不合作策略的时候，采取“针锋相对”策略一方的收益设为U2，另一方的收益设为U3；当对方也采取“针锋相对”策略的时候，双方在整个合作过程中都不会出现背叛现象，（合作，合作）将是双方的均衡策略选择，其收益均为U1。其中

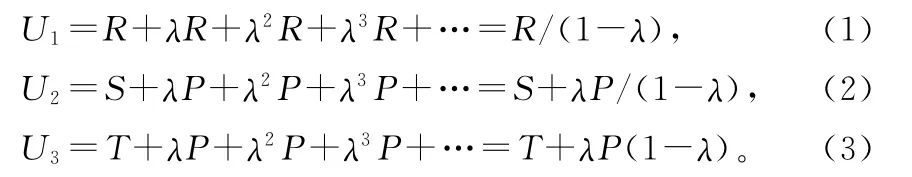
注：在无限次博弈的情况下，n被看成无穷大，则1－λn项被视为1，因此此项在上式中进行了省略。

二是冷酷触发战略，指的是一方开始时选择合作，如果对方也选择合作，就一直合作下去；如果对方选择不合作，自己下次也选择不合作，并且永远选择不合作。因为博弈没有最后阶段，所以不能运用逆向归纳法求解。在该战略下，首先背叛的一方的收益为U3，采取冷酷策略的一方的收益为U2。当对方一直采取合作策略的时候，博弈双方最终会在每个阶段都选择（合作，合作）的策略，双方的收益为U1。当对方也采取冷酷策略的时候，双方在整个合作过程中都不会出现背叛现象，（合作，合作）将是双方的均衡策略选择，其收益均为U1。

如何使（合作，合作）成为博弈均衡的结果呢？对博弈的任何一方而言重复选择合作策略的收益都必须要优于其他策略，即满足 Max（U1，U2，U3）＝U1，这时我们可以通过两种方法来考虑。

方法一：检查这种持续合作是否是一个均衡，可运用公式（今天背叛的收益与保持合作的收益差异≤今后保持合作收益与保持背叛收益差额再与博弈继续下去概率的乘积）来权衡是否（合作，合作）为博弈均衡结果。

方法二：因为T＞S，有U3＞U2。因此，只需要满足U1≥U3，即R／（1－λ）≥T＋λP／（1－λ），λ≥（T－R）／（T－P）时，冷酷战略才是无限次囚徒博弈的一个子博弈精炼纳什均衡，帕累托最优（合作，合作）是每个阶段的均衡结果，囚徒走出了一次性和有限次博弈时的困境。表明如果博弈重复无穷次且每个合作方有足够耐心，或者说是当博弈各方对未来的收益足够重视时，双方的合作关系才能建立和维持，短期的机会主义行为所得都将是微不足道的，参与人将积极为自己建立一个乐于合作的声誉，同时也会积极惩罚对方的机会主义行为。

四、规避和防范合作风险的规则和措施

尽管在供应链中各个企业相互独立，但它们却是相互依存的关系，企业之间的合作风险是无法避免的。要使供应链中各个企业保持相互合作，则必须寻求一些机制和标准对企业加以约束，以及采取一些措施规避和防范合作风险。

（一）建立“惩罚”或“奖赏”的合作机制

“惩罚”是一种消极激励，“奖赏”则是一种积极激励。“惩罚”和“奖赏”对促进合作能起到很重要激励作用。“惩罚”能够降低不合作者的收益，加大信用缺失等违法失信的机会成本，使合作各方清楚自己行为的后果，从而消除企业投机心理，使“不合作”成为“得不偿失”的选择；而“奖赏”能够提高合作者的收益，从而使得“合作”是一种“有利可图”的选择，为合作方的利益提供保证，诱导合作成员选择有利于共同利益的行为，从而加强合作成员的相互信任和密切合作。

在供应链联盟的合作博弈中，加入有形的保证金机制，即在合作前请第三方各收取合作双方保证金M作为以后的惩罚资金。若双方都采取积极合作的策略，则退回双方的保证金；若一方积极合作，另一方不合作或者是消极合作，则积极合作一方不仅能收回自己的保证金，而且还能得到对方的保证金；若双方都消极合作，则都失去各自的保证金。仍以先前考虑的两个企业（甲方与乙方）为例，新的得益矩阵则由表3所示。

表3 合作双方（甲方与乙方）双方采取收保证金后博弈分析

若R＋M＞T，即合作双方都缴纳了高于T－R单位的保证金时，此时（合作，合作）为唯一的纳什均衡，合作双方都更愿意合作。

（二）正确选择合作伙伴

在选择合作伙伴时应该首要考虑的就是该合作伙伴是否能以其核心优势来弥补本企业的不足，从而实现增强企业竞争力的目标；其次必须要准确地获取合作伙伴的服务质量、业务能力、声誉等实际情况的信息，否则由于信息不对称，极有可能造成双方在合作过程中的道德风险问题，使合作方因为眼前利益，而采取机会主义，使合作在中途夭折。只有这样，才能减少企业的监督成本，并在一定程度上避免双方在合作过程中的风险。

（三）构建信息与利益共享的合作机制

先前考虑的供应链合作模型的前提都是完美信息的动态博弈，如果是不完美信息博弈，结果将发生很大的变化，即如果合作双方对自己和对方的情况不了解，没有建立信息共享的合作机制，就会导致信息不对称，从而使先前讨论的博弈结果不正确。所以合作双方之间要进行良好的长期协商、保证信息的有效共享，使合作双方都能实时地了解到对方变化。另外要建立合理的收益分配机制与激励机制。合理的收益分配机制可以消除合作方的不公平感，减少机会主义行为，使双方都能在合作中看到更多获利点，从而积极加入合作中。

（四）运用供应链契约约束企业行为

供应链契约可以通过提供合适的信息和激励措施，保证买卖双方协调，优化销售渠道绩效的有关条款。即使供应链达不到最好的协调，也可能存在帕累托最优解，以保证每一方的利益至少不比原来差。而且供应契约可以以书面的形式保证合作企业的权利和义务，使这种权利和义务具有法律效应，这样即使信任机制不健全，也可以实现供应链合作的紧密性，加强信息共享，相互进行技术交流和提供技术支持。所以以供应链契约的形式固化合作关系十分必要。

（五）要向对方表明长期合作发展的愿景

前面我们讨论了一次性博弈、有限次数博弈和无限次数博弈，结果表明，一次性博弈和有限次数博弈常常不能达到双方合作的愿景。当自己向对方表明了将在下一次停止合作、或是表明自己将与对方合作有限次数时，对方将以消极的态度对待这些合作，以此来寻求自己的利益最大化。但当对方不知道合作将持续多久，为了获得“信誉”价值和长远的利益，往往会选择诚意合作来获得更多的长远利益。供应链中企业的联盟毕竟是由利益驱动的，当企业对长远利益不确定时，必然会增多追求短期利益的机会主义行为。所以向对方表明长期合作发展的愿景，在每次合作中改进双方行动，这对于建立长久的合作，为双方创造更多的价值十分重要。

［1］张维迎.博弈论与信息经济学［M］.上海：格致出版社，1996：25－42.

［2］骆温平.第三方物流［M］.北京：高等教育出版社，2007：49－51.

［3］李莹.供应链中供应商之间的纳什均衡博弈分析［J］.现代商贸工业，2013（5）：25－26.

［4］曹倩文，李明杰.供应链伙伴关系建立的合作博弈分析［J］.中国外资，2009（7）：168－169.

［5］汤鹏翔，王茜萌，高远洋.不同企业合作关系下供应链契约选择的博弈分析［J］.中国企业，2011（20）：89－93.

［6］Molander P.The optimal level of generosity in a selfish，uncertain environment［J］.Journal of Conflict Resolution，1985，29（4），611－618.

［7］Boerlijst M C，Nowak M A，Sigmund K.The logic of contrition［J］.Journal of Theoretical Biology，1997，185（3）：281－293.

［8］Johnston D A，Mccutcheon D M，Stuart F I，et al.Effects of supplier trust on performance of cooperative supplier relationships［J］.Journal of Operations Management，2004，22（1）：23－38.